Cifrado de bloque

En criptografía, un cifrado de bloque es un algoritmo determinista que opera en grupos de bits de longitud fija, llamados bloques. Los cifrados de bloque son componentes elementales especificados en el diseño de muchos protocolos criptográficos y se utilizan ampliamente para cifrar grandes cantidades de datos, incluso en protocolos de intercambio de datos. Un cifrado de bloque utiliza bloques como una transformación invariable.

Incluso un cifrado de bloque seguro es adecuado para el cifrado de un solo bloque de datos a la vez, utilizando una clave fija. Se han diseñado una multitud de modos de operación para permitir su uso repetido de forma segura para lograr los objetivos de seguridad de confidencialidad y autenticidad. Sin embargo, los cifrados de bloques también pueden aparecer como bloques de construcción en otros protocolos criptográficos, como funciones hash universales y generadores de números pseudoaleatorios.

Definición

Un cifrado de bloque consta de dos algoritmos emparejados, uno para el cifrado, E, y el otro para el descifrado, D. Ambos algoritmos aceptan dos entradas: un bloque de entrada de tamaño n bits y una clave de tamaño k bits; y ambos generan un bloque de salida de n bits. El algoritmo de descifrado D se define como la función inversa del cifrado, es decir, D = E⁻¹. Más formalmente, un cifrado de bloque se especifica mediante una función de cifrado

EK()P):=E()K,P):{}0,1}k× × {}0,1}n→ → {}0,1}n,{displaystyle E_{K}(P):=E(K,P):{0,1}times {0,1}n}rightarrow {0,1} {n}

que toma como entrada una clave K, de longitud en bits k (llamada clave size), y una cadena de bits P, de longitud n (llamada tamaño de bloque), y devuelve una cadena C de n bits. P se denomina texto sin formato y C se denomina texto cifrado. Para cada K, la función E_K(P) es necesario para ser una asignación invertible en {0,1}ⁿ. La inversa de E se define como una función

EK− − 1()C):=DK()C)=D()K,C):{}0,1}k× × {}0,1}n→ → {}0,1}n,{displaystyle ¿Qué?

tomando una clave K y un texto cifrado C para devolver un valor de texto sin formato P, tal que

О О P:DK()EK()P))=P.{displaystyle forall P:D_{K}(E_{K}(P)= P.}

Por ejemplo, un algoritmo de cifrado de bloque podría tomar un bloque de texto sin formato de 128 bits como entrada y generar un bloque de texto cifrado de 128 bits correspondiente. La transformación exacta se controla mediante una segunda entrada: la clave secreta. El descifrado es similar: el algoritmo de descifrado toma, en este ejemplo, un bloque de texto cifrado de 128 bits junto con la clave secreta y produce el bloque original de texto sin formato de 128 bits.

Para cada clave K, E_K es una permutación (una cartografía bijeactiva) sobre el conjunto de bloques de entrada. Cada clave selecciona una permutación del conjunto de ()2n)!{displaystyle (2^{n})} permutaciones posibles.

Historia

El diseño moderno de cifrados de bloque se basa en el concepto de un cifrado de producto iterado. En su publicación seminal de 1949, Teoría de la comunicación de los sistemas secretos, Claude Shannon analizó los cifrados de productos y los sugirió como un medio para mejorar la seguridad mediante la combinación de operaciones simples como sustituciones y permutaciones. Los cifrados de productos iterados llevan a cabo el cifrado en varias rondas, cada una de las cuales utiliza una subclave diferente derivada de la clave original. Una implementación generalizada de tales cifrados, llamada red Feistel en honor a Horst Feistel, se implementa notablemente en el cifrado DES. Muchas otras realizaciones de cifrados de bloque, como el AES, se clasifican como redes de sustitución-permutación.

La raíz de todos los formatos de bloques criptográficos utilizados en el Estándar de seguridad de datos de la industria de tarjetas de pago (PCI DSS) y los estándares del Instituto Nacional Estadounidense de Estándares (ANSI) se encuentra en Atalla Key Block (AKB), que fue una innovación clave de Atalla. Box, el primer módulo de seguridad de hardware (HSM). Fue desarrollado en 1972 por Mohamed M. Atalla, fundador de Atalla Corporation (ahora Utimaco Atalla), y lanzado en 1973. El AKB era un bloque clave, que se requiere para intercambiar de forma segura claves simétricas o PIN con otros actores de la industria bancaria.. Este intercambio seguro se realiza utilizando el formato AKB. Atalla Box protegió más del 90 % de todas las redes de cajeros automáticos en funcionamiento a partir de 1998, y los productos Atalla aún protegen la mayoría de las transacciones de cajeros automáticos del mundo a partir de 2014.

La publicación del cifrado DES por parte de la Oficina Nacional de Estándares de los Estados Unidos (posteriormente, el Instituto Nacional de Estándares y Tecnología de los Estados Unidos, NIST) en 1977 fue fundamental en la comprensión pública del diseño moderno de cifrado de bloques. También influyó en el desarrollo académico de los ataques criptoanalíticos. Tanto el criptoanálisis diferencial como el lineal surgieron de los estudios sobre el diseño DES. A partir de 2016, existe una paleta de técnicas de ataque contra las cuales un cifrado de bloque debe ser seguro, además de ser robusto contra ataques de fuerza bruta.

Diseño

Cifrados de bloques iterados

La mayoría de los algoritmos de cifrado de bloques se clasifican como cifrados de bloques iterados, lo que significa que transforman bloques de texto sin formato de tamaño fijo en bloques de texto cifrado de tamaño idéntico, mediante la aplicación repetida de una transformación invertible conocida como función redonda, con cada iteración denominada ronda.

Por lo general, la función redonda R toma diferentes claves redondas K_i como segunda entrada, que se derivan de la clave original:

Mi=RKi()Mi− − 1){displaystyle ¿Qué?

Donde M0{displaystyle M_{0} es el texto y Mr{displaystyle M_{r} el cifertexto, con r siendo el número de rondas.

Con frecuencia, además de esto, se utiliza el blanqueamiento de llaves. Al principio y al final, los datos se modifican con material clave (a menudo con XOR, pero también se usan operaciones aritméticas simples como sumar y restar):

M0=M⊕ ⊕ K0{displaystyle M_{0}=Moplus K_{0}

Mi=RKi()Mi− − 1);i=1...... r{displaystyle M_{i}=R_{K_}(M_{i-1});;i=1dots r}

C=Mr⊕ ⊕ Kr+1{displaystyle C=M_{r}oplus K_{r+1}}

Dado uno de los esquemas de diseño de cifrado de bloques iterados estándar, es bastante fácil construir un cifrado de bloques que sea criptográficamente seguro, simplemente usando una gran cantidad de rondas. Sin embargo, esto hará que el cifrado sea ineficiente. Por lo tanto, la eficiencia es el criterio de diseño adicional más importante para los cifrados profesionales. Además, un buen cifrado de bloques está diseñado para evitar ataques de canal lateral, como la predicción de ramificación y los accesos a la memoria dependientes de la entrada que pueden filtrar datos secretos a través del estado de la memoria caché o el tiempo de ejecución. Además, el cifrado debe ser conciso, para pequeñas implementaciones de hardware y software. Finalmente, el cifrado debe ser fácilmente criptoanalizado, de modo que se pueda mostrar a cuántas rondas se debe reducir el cifrado, para que funcionen los ataques criptográficos existentes y, a la inversa, que se pueda demostrar que el número de rondas reales es lo suficientemente grande como para protegerse contra ellos.

Redes de sustitución-permutación

Un bosquejo de una red de sustitución-permutación con 3 rondas, encriptando un bloque de texto claro de 16 bits en un bloque de texto de 16 bits. Los S-boxes son los S_i, las cajas P son las mismas P, y las llaves redondas son K_i.

Un tipo importante de cifrado de bloque iterado conocido como red de sustitución-permutación (SPN) toma un bloque del texto sin formato y la clave como entradas y aplica varias rondas alternas que consisten en una etapa de sustitución seguida por una etapa de permutación—para producir cada bloque de salida de texto cifrado. La etapa de sustitución no lineal mezcla los bits clave con los del texto sin formato, creando la confusión de Shannon. La etapa de permutación lineal luego disipa las redundancias, creando difusión.

Un cuadro de sustitución (S-box) sustituye un pequeño bloque de bits de entrada con otro bloque de bits de salida. Esta sustitución debe ser de uno a uno, para garantizar la invertibilidad (por lo tanto, el descifrado). Un S-box seguro tendrá la propiedad de que cambiar un bit de entrada cambiará aproximadamente la mitad de los bits de salida en promedio, exhibiendo lo que se conoce como el efecto de avalancha, es decir tiene la propiedad de que cada bit de salida dependerá de cada bit de entrada.

Un cuadro de permutación (P-box) es una permutación de todos los bits: toma las salidas de todos los S-boxes de una ronda, permuta los bits y los introduce en el S -cajas de la siguiente ronda. Un buen P-box tiene la propiedad de que los bits de salida de cualquier S-box se distribuyen a tantas entradas de S-box como sea posible.

En cada ronda, la clave de ronda (obtenida de la clave con algunas operaciones simples, por ejemplo, usando S-boxes y P-boxes) se combina usando alguna operación de grupo, normalmente XOR.

El descifrado se realiza simplemente invirtiendo el proceso (usando los inversos de los S-boxes y P-boxes y aplicando las claves redondas en orden inverso).

Cifrados Feistel

Muchos bloques de cifers, como DES y Blowfish utilizan estructuras conocidas como Cifras feisteles

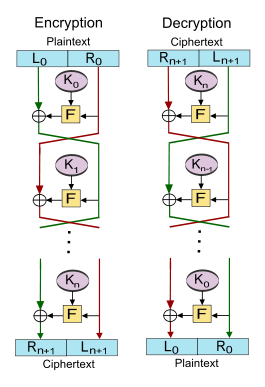
En un cifrado Feistel, el bloque de texto sin formato que se va a cifrar se divide en dos mitades del mismo tamaño. La función de ronda se aplica a una mitad, usando una subclave, y luego la salida se XOR con la otra mitad. Luego se intercambian las dos mitades.

Vamos F{displaystyle {rm {f}} ser la función redonda y dejar K0,K1,...... ,Kn{displaystyle K_{0},K_{1},ldots K_{n} ser los sub-keys para las rondas 0,1,...... ,n{displaystyle 0,1,ldotsn} respectivamente.

Entonces el funcionamiento básico es el siguiente:

Dividir el bloque de texto en dos partes iguales (L0{displaystyle L_{0}, R0{displaystyle R_{0})

Para cada ronda i=0,1,...... ,n{displaystyle i=0,1,dotsn}, computación

Li+1=Ri{displaystyle L_{i+1}=R_{i},}

Ri+1=Li⊕ ⊕ F()Ri,Ki){displaystyle ¿Qué?.

Entonces el cifertexto es ()Rn+1,Ln+1){displaystyle (R_{n+1},L_{n+1})}.

Decryption of a ciphertext ()Rn+1,Ln+1){displaystyle (R_{n+1},L_{n+1})} se logra por computación para i=n,n− − 1,...... ,0{displaystyle i=n,n-1,ldots0}

Ri=Li+1{displaystyle R_{i}=L_{i+1},}

Li=Ri+1⊕ ⊕ F()Li+1,Ki){displaystyle L_{i}=R_{i+1}oplus {rm {F}(L_{i+1},K_{i})}.

Entonces... ()L0,R0){displaystyle (L_{0},R_{0})} es el texto de nuevo.

Una ventaja del modelo Feistel en comparación con una red de sustitución-permutación es que la función redonda F{displaystyle {rm {f}} no tiene que ser invertible.

Cifrados Lai-Massey

El plan Lai-Massey. El cifrado arquetípico que utiliza es IDEA.

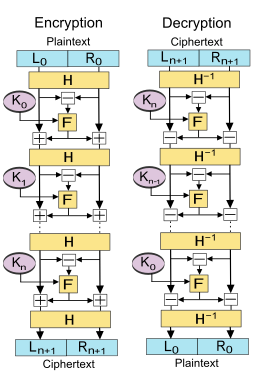
El esquema Lai-Massey ofrece propiedades de seguridad similares a las de la estructura Feistel. También comparte su ventaja de que la función redonda F{displaystyle mathrm {F} no tiene que ser invertible. Otra similitud es que también divide el bloque de entrada en dos piezas iguales. Sin embargo, la función redonda se aplica a la diferencia entre los dos, y el resultado se añade a ambos medio bloques.

Vamos F{displaystyle mathrm {F} ser la función redonda y H{displaystyle mathrm {H} una función media ronda y dejar K0,K1,...... ,Kn{displaystyle K_{0},K_{1},ldots K_{n} ser los sub-keys para las rondas 0,1,...... ,n{displaystyle 0,1,ldotsn} respectivamente.

Entonces el funcionamiento básico es el siguiente:

Dividir el bloque de texto en dos partes iguales (L0{displaystyle L_{0}, R0{displaystyle R_{0})

Para cada ronda i=0,1,...... ,n{displaystyle i=0,1,dotsn}, computación

()Li+1.,Ri+1.)=H()Li.+Ti,Ri.+Ti),{displaystyle (L_{i+1}',R_{i+1}')=mathrm {H} (L_{i}'+T_{i},R_{i}'+T_{i}),}

Donde Ti=F()Li.− − Ri.,Ki){displaystyle T_{i}=mathrm {F} (L_{i}'-R_{i}',K_{i}} y ()L0.,R0.)=H()L0,R0){displaystyle (L_{0}',R_{0}')=mathrm {H} (L_{0},R_{0})}

Entonces el cifertexto es ()Ln+1,Rn+1)=()Ln+1.,Rn+1.){displaystyle (L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')}.

Decryption of a ciphertext ()Ln+1,Rn+1){displaystyle (L_{n+1},R_{n+1})} se logra por computación para i=n,n− − 1,...... ,0{displaystyle i=n,n-1,ldots0}

()Li.,Ri.)=H− − 1()Li+1.− − Ti,Ri+1.− − Ti){displaystyle (L_{i}',R_{i}')=mathrm {H} {{-1}(L_{i+1}'-T_{i},R_{i+1}'-T_{i}

Donde Ti=F()Li+1.− − Ri+1.,Ki){displaystyle T_{i}=mathrm {F} (L_{i+1}'-R_{i+1}',K_{i}) } y ()Ln+1.,Rn+1.)=H− − 1()Ln+1,Rn+1){displaystyle (L_{n+1}',R_{n+1}')=mathrm {H} ^{-1}(L_{n+1},R_{n+1}}}

Entonces... ()L0,R0)=()L0.,R0.){displaystyle (L_{0},R_{0}=(L_{0}',R_{0}')} es el texto de nuevo.

Operaciones

ARX (añadir–rotar–XOR)

Muchos cifrados de bloques y hashes modernos son algoritmos ARX: su función de ronda implica solo tres operaciones: (A) suma modular, (R) rotación con cantidades de rotación fijas y (X) XOR. Los ejemplos incluyen ChaCha20, Speck, XXTEA y BLAKE. Muchos autores dibujan una red ARX, una especie de diagrama de flujo de datos, para ilustrar esta función redonda.

Estas operaciones ARX son populares porque son relativamente rápidas y económicas en hardware y software, su implementación puede ser extremadamente simple y también porque se ejecutan en tiempo constante y, por lo tanto, son inmunes a los ataques de tiempo. La técnica de criptoanálisis rotacional intenta atacar tales funciones redondas.

Otras operaciones

Otras operaciones que se usan a menudo en los cifrados de bloque incluyen rotaciones dependientes de datos como en RC5 y RC6, un cuadro de sustitución implementado como una tabla de búsqueda como en el Estándar de cifrado de datos y el Estándar de cifrado avanzado, un cuadro de permutación y multiplicación como en IDEA.

Modos de funcionamiento

Encriptación insegura de una imagen como resultado de la codificación electrónica del modo codebook (ECB).

Un cifrado de bloque por sí mismo permite el cifrado solo de un único bloque de datos de la longitud del bloque del cifrado. Para un mensaje de longitud variable, los datos deben dividirse primero en bloques de cifrado separados. En el caso más simple, conocido como modo de libro de códigos electrónico (ECB), primero se divide un mensaje en bloques separados del tamaño del bloque del cifrado (posiblemente extendiendo el último bloque con bits de relleno), y luego cada bloque se cifra y descifra. independientemente. Sin embargo, un método tan ingenuo es generalmente inseguro porque los bloques iguales de texto sin formato siempre generarán bloques iguales de texto cifrado (para la misma clave), por lo que los patrones en el mensaje de texto sin formato se vuelven evidentes en la salida del texto cifrado.

Para superar esta limitación, se han diseñado y especificado varios modos de operación de cifrado de bloques en recomendaciones nacionales como NIST 800-38A y BSI TR-02102 y estándares internacionales como ISO/IEC 10116. El concepto general es utilice la aleatorización de los datos de texto sin formato en función de un valor de entrada adicional, con frecuencia denominado vector de inicialización, para crear lo que se denomina cifrado probabilístico. En el popular modo de encadenamiento de bloques de cifrado (CBC), para que el cifrado sea seguro, el vector de inicialización que se pasa junto con el mensaje de texto sin formato debe ser un valor aleatorio o pseudoaleatorio, que se agrega de manera exclusiva al primer bloque de texto sin formato antes está siendo encriptado. El bloque de texto cifrado resultante se usa luego como el nuevo vector de inicialización para el siguiente bloque de texto sin formato. En el modo de retroalimentación de cifrado (CFB), que emula un cifrado de flujo de sincronización automática, el vector de inicialización se cifra primero y luego se agrega al bloque de texto sin formato. El modo de retroalimentación de salida (OFB) cifra repetidamente el vector de inicialización para crear un flujo de clave para la emulación de un cifrado de flujo síncrono. El modo de contador más nuevo (CTR) crea de manera similar un flujo de claves, pero tiene la ventaja de que solo necesita valores únicos y no (pseudo) aleatorios como vectores de inicialización; la aleatoriedad necesaria se deriva internamente utilizando el vector de inicialización como un contador de bloques y cifrando este contador para cada bloque.

Desde un punto de vista teórico de la seguridad, los modos de operación deben proporcionar lo que se conoce como seguridad semántica. Informalmente, significa que dado un texto cifrado bajo una clave desconocida, prácticamente no se puede derivar ninguna información del texto cifrado (aparte de la longitud del mensaje) sobre lo que uno hubiera sabido sin ver el texto cifrado. Se ha demostrado que todos los modos discutidos anteriormente, con la excepción del modo ECB, proporcionan esta propiedad bajo los llamados ataques de texto sin formato elegidos.

Relleno

Algunos modos, como el modo CBC, solo funcionan en bloques completos de texto sin formato. Simplemente extender el último bloque de un mensaje con bits cero es insuficiente ya que no permite que un receptor distinga fácilmente los mensajes que difieren solo en la cantidad de bits de relleno. Más importante aún, una solución tan simple da lugar a ataques de oráculo de relleno muy eficientes. Por lo tanto, se necesita un esquema de relleno adecuado para extender el último bloque de texto sin formato al tamaño del bloque del cifrado. Si bien se ha demostrado que muchos esquemas populares descritos en estándares y en la literatura son vulnerables a los ataques de oráculo de relleno, una solución que agrega un bit y luego extiende el último bloque con cero bits, estandarizada como "método de relleno 2& #34; en ISO/IEC 9797-1, ha demostrado ser seguro contra estos ataques.

Cripanálisis

Ataques de fuerza bruta

Esta propiedad hace que la seguridad del cifrado se degrade cuadráticamente y debe tenerse en cuenta al seleccionar un tamaño de bloque. Sin embargo, existe una compensación, ya que los tamaños de bloque grandes pueden hacer que el funcionamiento del algoritmo se vuelva ineficiente. Los cifrados de bloque anteriores, como el DES, generalmente seleccionaban un tamaño de bloque de 64 bits, mientras que los diseños más nuevos, como el AES, admiten tamaños de bloque de 128 bits o más, y algunos cifrados admiten una variedad de tamaños de bloque diferentes.

Criptoanálisis diferencial

Criptoanálisis lineal

El criptoanálisis lineal es una forma de criptoanálisis basada en encontrar aproximaciones afines a la acción de un cifrado. El criptoanálisis lineal es uno de los dos ataques más utilizados contra los cifrados en bloque; el otro es el criptoanálisis diferencial.

El descubrimiento se atribuye a Mitsuru Matsui, quien fue el primero en aplicar la técnica al cifrado FEAL (Matsui y Yamagishi, 1992).

Criptoanálisis integral

El criptoanálisis integral es un ataque criptoanalítico que es particularmente aplicable a los cifrados de bloque basados en redes de sustitución-permutación. A diferencia del criptoanálisis diferencial, que usa pares de textos sin formato elegidos con una diferencia XOR fija, el criptoanálisis integral usa conjuntos o incluso conjuntos múltiples de textos sin formato elegidos, de los cuales una parte se mantiene constante y otra parte varía a través de todas las posibilidades. Por ejemplo, un ataque podría usar 256 textos sin formato elegidos que tienen todos menos 8 de sus bits iguales, pero todos difieren en esos 8 bits. Tal conjunto necesariamente tiene una suma XOR de 0, y las sumas XOR de los correspondientes conjuntos de textos cifrados brindan información sobre la operación del cifrado. Este contraste entre las diferencias de pares de textos y las sumas de conjuntos de textos más grandes inspiró el nombre de "criptoanálisis integral", tomando prestada la terminología del cálculo.

Otras técnicas

El desarrollo del ataque de boomerang permitió aplicar técnicas diferenciales de criptanálisis a muchos cifrados que anteriormente se habían considerado seguros contra ataques diferenciales

Además del criptoanálisis lineal y diferencial, existe un catálogo creciente de ataques: criptoanálisis diferencial truncado, criptoanálisis diferencial parcial, criptoanálisis integral, que abarca ataques cuadrados e integrales, ataques deslizantes, ataques boomerang, el ataque XSL, criptoanálisis diferencial imposible y ataques algebraicos. Para que un nuevo diseño de cifrado de bloques tenga credibilidad, debe demostrar evidencia de seguridad contra ataques conocidos.

Seguridad demostrable

Cuando se usa un cifrado de bloque en un modo de operación dado, el algoritmo resultante idealmente debería ser tan seguro como el propio cifrado de bloque. ECB (discutido anteriormente) carece enfáticamente de esta propiedad: independientemente de cuán seguro sea el cifrado de bloque subyacente, el modo ECB puede ser atacado fácilmente. Por otro lado, se puede demostrar que el modo CBC es seguro bajo el supuesto de que el cifrado de bloque subyacente también es seguro. Tenga en cuenta, sin embargo, que hacer afirmaciones como esta requiere definiciones matemáticas formales de lo que significa que un algoritmo de cifrado o un cifrado de bloques "estén seguros". Esta sección describe dos nociones comunes sobre las propiedades que debe tener un cifrado de bloque. Cada uno corresponde a un modelo matemático que se puede usar para probar propiedades de algoritmos de nivel superior, como CBC.

Este enfoque general de la criptografía (demostrar que los algoritmos de alto nivel (como CBC) son seguros bajo suposiciones explícitas con respecto a sus componentes (como un cifrado de bloque)) se conoce como seguridad demostrable.

Modelo estándar

De manera informal, un cifrado de bloque es seguro en el modelo estándar si un atacante no puede distinguir la diferencia entre el cifrado de bloque (equipado con una clave aleatoria) y una permutación aleatoria.

Para ser un poco más preciso, sea E un cifrado de bloques de n bits. Imaginamos el siguiente juego:

1. La persona que ejecuta el juego cambia una moneda.
   • Si la moneda cae en la cabeza, elige una llave al azar K y define la función f = E_K.
   • Si la moneda cae en las colas, elige una permutación aleatoria π sobre el conjunto de n-bit strings, y define la función f = π.
2. El atacante elige un n- cuerda de bit X, y la persona que ejecuta el juego le dice el valor de f()X).
3. Paso 2 se repite un total de q veces. (Cada uno de estos q interacciones es un query.)
4. El atacante adivina cómo aterrizó la moneda. Gana si su suposición es correcta.

El atacante, que podemos modelar como un algoritmo, se denomina adversario. La función f (que el adversario pudo consultar) se denomina oráculo.

Tenga en cuenta que un adversario puede asegurar trivialmente un 50 % de posibilidades de ganar simplemente adivinando al azar (o incluso, por ejemplo, siempre adivinando "cara"). Por lo tanto, sea P_E(A) la probabilidad de que el adversario A gana este juego contra E, y define la ventaja de A como 2(P _E(A) − 1/2). De ello se deduce que si A adivina al azar, su ventaja será 0; por otro lado, si A siempre gana, entonces su ventaja es 1. El cifrado de bloque E es una permutación pseudo-aleatoria (PRP) si ningún adversario tiene una ventaja significativamente mayor que 0, dadas las restricciones específicas sobre q y el tiempo de ejecución del adversario. Si en el Paso 2 anterior, los adversarios tienen la opción de aprender f⁻¹(X) en lugar de f(X) (pero aún tienen solo pequeñas ventajas), entonces E es un PRP fuerte (SPRP). Un adversario es no adaptativo si elige todos los valores q para X antes de que comience el juego (es decir, no utiliza ninguna información recopilada de consultas anteriores para elegir cada X a medida que avanza).

Estas definiciones han demostrado ser útiles para analizar varios modos de operación. Por ejemplo, se puede definir un juego similar para medir la seguridad de un algoritmo de cifrado basado en cifrado de bloques y luego tratar de mostrar (a través de un argumento de reducción) que la probabilidad de que un adversario gane este nuevo juego no es mucho mayor que P_E(A) para alguna A. (La reducción generalmente proporciona límites en q y el tiempo de ejecución de A). De manera equivalente, si P_E(A) es pequeño para todos los A relevantes, entonces ningún atacante tiene una probabilidad significativa de ganar el nuevo juego. Esto formaliza la idea de que el algoritmo de nivel superior hereda la seguridad del cifrado de bloque.

Modelo de cifrado ideal

Evaluación práctica

En la práctica, los cifrados de bloque se pueden evaluar de acuerdo con múltiples criterios. Los factores comunes incluyen:

• Parámetros clave, como su tamaño clave y tamaño de bloque, ambos proporcionan un límite superior en la seguridad del cifrado.
• El nivel estimado de seguridad, que se basa en la confianza obtenida en el diseño de cifrado de bloque después de que ha resistido en gran medida grandes esfuerzos en criptanálisis con el tiempo, la solidez matemática del diseño, y la existencia de ataques prácticos o certificantes.
• El cifrado complejidad y su idoneidad para la implementación en hardware o software. Las implementaciones de hardware pueden medir la complejidad en términos de recuento de puertas o consumo de energía, que son parámetros importantes para dispositivos con restricciones de recursos.
• El cifrado rendimiento en términos de rendimiento de procesamiento en varias plataformas, incluyendo sus requisitos de memoria.
• El Costo del cifrado, que se refiere a los requisitos de concesión de licencias que puedan aplicarse debido a los derechos de propiedad intelectual.
• El flexibilidad del cifrado, que incluye su capacidad para soportar múltiples tamaños clave y longitudes de bloque.

Cifrados de bloques notables

Lucifer / DES

Por lo general, se considera que Lucifer es el primer cifrado de bloque civil, desarrollado en IBM en la década de 1970 en base al trabajo realizado por Horst Feistel. Se adoptó una versión revisada del algoritmo como estándar federal de procesamiento de información del gobierno de EE. UU.: FIPS PUB 46 Data Encryption Standard (DES). Fue elegido por la Oficina Nacional de Normas de EE. UU. (NBS) después de una invitación pública para presentaciones y algunos cambios internos por parte de la NBS (y, potencialmente, la NSA). DES fue lanzado al público en 1976 y ha sido ampliamente utilizado.

DES fue diseñado para, entre otras cosas, resistir un determinado ataque criptoanalítico conocido por la NSA y redescubierto por IBM, aunque desconocido públicamente hasta que Eli Biham y Adi Shamir lo redescubrieron nuevamente y lo publicaron a fines de la década de 1980. La técnica se denomina criptoanálisis diferencial y sigue siendo uno de los pocos ataques generales contra los cifrados en bloque; el criptoanálisis lineal es otro, pero puede haber sido desconocido incluso para la NSA, antes de su publicación por Mitsuru Matsui. DES generó una gran cantidad de otros trabajos y publicaciones en criptografía y criptoanálisis en la comunidad abierta e inspiró muchos diseños de cifrado nuevos.

DES tiene un tamaño de bloque de 64 bits y un tamaño de clave de 56 bits. Los bloques de 64 bits se volvieron comunes en los diseños de cifrado de bloques después de DES. La longitud de la clave dependía de varios factores, incluida la regulación gubernamental. Muchos observadores en la década de 1970 comentaron que la longitud de clave de 56 bits utilizada para DES era demasiado corta. Con el paso del tiempo, su insuficiencia se hizo evidente, especialmente después de que Electronic Frontier Foundation demostrara en 1998 una máquina de propósito especial diseñada para romper DES. Una extensión de DES, Triple DES, cifra triplemente cada bloque con dos claves independientes (clave de 112 bits y seguridad de 80 bits) o tres claves independientes (clave de 168 bits y seguridad de 112 bits). Fue ampliamente adoptado como reemplazo. A partir de 2011, la versión de tres claves todavía se considera segura, aunque los estándares del Instituto Nacional de Estándares y Tecnología (NIST) ya no permiten el uso de la versión de dos claves en nuevas aplicaciones, debido a su nivel de seguridad de 80 bits.

IDEA

El Algoritmo Internacional de Cifrado de Datos (IDEA) es un cifrado de bloque diseñado por James Massey de ETH Zurich y Xuejia Lai; se describió por primera vez en 1991, como un reemplazo previsto para DES.

IDEA opera en bloques de 64 bits usando una clave de 128 bits y consta de una serie de ocho transformaciones idénticas (una redonda) y una transformación de salida (la media vuelta). Los procesos de cifrado y descifrado son similares. IDEA deriva gran parte de su seguridad al intercalar operaciones de diferentes grupos (suma y multiplicación modular, y exclusivo o (XOR) bit a bit, que son algebraicamente "incompatibles" en algún sentido.

Los diseñadores analizaron IDEA para medir su fuerza contra el criptoanálisis diferencial y concluyeron que es inmune bajo ciertas suposiciones. No se han informado debilidades lineales o algebraicas satisfactorias. A partir de 2012, el mejor ataque que se aplica a todas las teclas puede romper la IDEA completa de 8.5 rondas usando un ataque de bicliques estrechos unas cuatro veces más rápido que la fuerza bruta.

RC5

Una ronda (dos medias rondas) de la caja RC5

RC5 es un cifrado de bloque diseñado por Ronald Rivest en 1994 que, a diferencia de muchos otros cifrados, tiene un tamaño de bloque variable (32, 64 o 128 bits), tamaño de clave (0 a 2040 bits) y número de rondas (0 a 255). La elección de parámetros sugerida originalmente era un tamaño de bloque de 64 bits, una clave de 128 bits y 12 rondas.

Una característica clave de RC5 es el uso de rotaciones dependientes de datos; uno de los objetivos de RC5 era impulsar el estudio y la evaluación de tales operaciones como una primitiva criptográfica. RC5 también consta de una serie de adiciones modulares y XOR. La estructura general del algoritmo es una red tipo Feistel. Las rutinas de cifrado y descifrado se pueden especificar en unas pocas líneas de código. El programa clave, sin embargo, es más complejo, expandiendo la clave utilizando una función esencialmente unidireccional con las expansiones binarias tanto de e como de la proporción áurea como fuentes de "números sin nada en la manga". La tentadora simplicidad del algoritmo junto con la novedad de las rotaciones dependientes de los datos ha convertido a RC5 en un atractivo objeto de estudio para los criptoanalistas.

RC5 de 12 rondas (con bloques de 64 bits) es susceptible a un ataque diferencial utilizando 2⁴⁴ textos sin formato elegidos. Se sugieren 18-20 rondas como protección suficiente.

Rijndael / AES

El cifrado Rijndael desarrollado por los criptógrafos belgas, Joan Daemen y Vincent Rijmen, fue uno de los diseños de la competencia para reemplazar a DES. Ganó la competencia pública de 5 años para convertirse en AES (Advanced Encryption Standard).

Adoptado por NIST en 2001, AES tiene un tamaño de bloque fijo de 128 bits y un tamaño de clave de 128, 192 o 256 bits, mientras que Rijndael se puede especificar con tamaños de bloque y clave en cualquier múltiplo de 32 bits, con un mínimo de 128 bits. El tamaño del bloque tiene un máximo de 256 bits, pero el tamaño de la clave no tiene un máximo teórico. AES opera en una matriz de bytes de orden principal de 4 × 4 columnas, denominada estado (las versiones de Rijndael con un tamaño de bloque más grande tienen columnas adicionales en el estado).

Pez globo

Blowfish es un cifrado de bloque, diseñado en 1993 por Bruce Schneier e incluido en una gran cantidad de conjuntos de cifrado y productos de cifrado. Blowfish tiene un tamaño de bloque de 64 bits y una longitud de clave variable desde 1 bit hasta 448 bits. Es un cifrado Feistel de 16 rondas y utiliza grandes S-boxes dependientes de claves. Las características notables del diseño incluyen las cajas S dependientes de la llave y un programa de llaves muy complejo.

Fue diseñado como un algoritmo de propósito general, pensado como una alternativa al antiguo DES y libre de los problemas y restricciones asociados con otros algoritmos. En el momento en que se lanzó Blowfish, muchos otros diseños eran propietarios, estaban gravados por patentes o eran secretos comerciales/gubernamentales. Schneier ha declarado que "Blowfish no está patentado y seguirá siéndolo en todos los países. Por la presente, el algoritmo se coloca en el dominio público y cualquier persona puede utilizarlo libremente." Lo mismo se aplica a Twofish, un algoritmo sucesor de Schneier.

Generalizaciones

Cifrados de bloque modificables

M. Liskov, R. Rivest y D. Wagner han descrito una versión generalizada de cifrados de bloques llamada "tweakable" cifrados en bloque. Un cifrado de bloque ajustable acepta una segunda entrada llamada tweak junto con su entrada habitual de texto sin formato o texto cifrado. El ajuste, junto con la clave, selecciona la permutación calculada por el cifrado. Si cambiar los ajustes es lo suficientemente ligero (en comparación con una operación de configuración de teclas generalmente bastante costosa), entonces se hacen posibles algunos modos de operación nuevos e interesantes. El artículo sobre la teoría del cifrado de disco describe algunos de estos modos.

Cifrado que conserva el formato

Los cifrados de bloque funcionan tradicionalmente sobre un alfabeto binario. Es decir, tanto la entrada como la salida son cadenas binarias, que consisten en n ceros y unos. En algunas situaciones, sin embargo, uno puede desear tener un cifrado de bloques que funcione con algún otro alfabeto; por ejemplo, cifrar números de tarjetas de crédito de 16 dígitos de tal manera que el texto cifrado también sea un número de 16 dígitos podría facilitar la adición de una capa de cifrado al software heredado. Este es un ejemplo de cifrado que conserva el formato. En términos más generales, el cifrado que conserva el formato requiere una permutación con clave en algún lenguaje finito. Esto hace que los esquemas de cifrado que preservan el formato sean una generalización natural de los cifrados de bloques (modificables). Por el contrario, los esquemas de cifrado tradicionales, como CBC, no son permutaciones porque el mismo texto sin formato puede cifrarse en múltiples textos cifrados diferentes, incluso cuando se usa una clave fija.

Relación con otras primitivas criptográficas

Los cifrados de bloque se pueden usar para construir otras primitivas criptográficas, como las siguientes. Para que estas otras primitivas sean criptográficamente seguras, se debe tener cuidado para construirlas de la manera correcta.

• Los cifrados de corriente se pueden construir utilizando cifrados de bloques. El modo OFB-mode y CTR son modos de bloque que convierten un cifrado de bloque en un cifrado de flujo.
• Las funciones de hash crioptográficas se pueden construir utilizando cifers bloque. Vea la función de compresión de un solo sentido para descripciones de varios métodos de este tipo. Los métodos se asemejan a los modos de operación bloque cipher generalmente utilizados para la encriptación.
• Se pueden construir generadores de números de pseudorandones (CSPRNG) con cifrado de bloques.
• Las permutaciones de pseudopreservación seguras de conjuntos finitos de tamaño arbitrario se pueden construir con cifrados de bloques; véase Encriptación de Preservación de Formato.
• Una permutación impredecible conocida públicamente combinada con blanqueamiento clave es suficiente para construir un cifrado de bloques, como el cifer de un solo llave Even-Mansour, quizás el más simple posible cipher de bloque provablemente seguro.
• Los códigos de autenticación de mensajes (MAC) a menudo se construyen a partir de cifrados bloque. CBC-MAC, OMAC y PMAC son tales MAC.
• La encriptación autenticada también se construye a partir de cifers bloque. Significa encriptar y MAC al mismo tiempo. Esto es para ofrecer confidencialidad y autenticación. CCM, EAX, GCM y OCB son modos de cifrado autenticados.

Así como los cifrados de bloque se pueden usar para construir funciones hash, como SHA-1 y SHA-2 se basan en cifrados de bloque que también se usan de forma independiente como SHACAL, las funciones hash se pueden usar para construir cifrados de bloque. Ejemplos de tales cifrados de bloque son BEAR y LION.