Ciencias formales

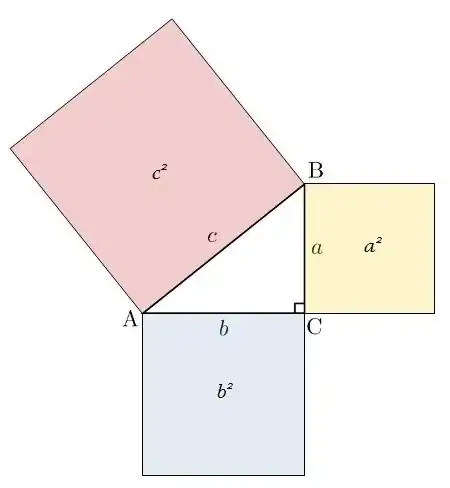
La ciencia formal es una rama de la ciencia que estudia las disciplinas del lenguaje formal relacionadas con los sistemas formales, como la lógica, las matemáticas, la geometría, la estadística, la informática teórica, la inteligencia artificial, la teoría de la información, la teoría de juegos, la teoría de sistemas, la teoría de decisiones y la lingüística teórica. Mientras que las ciencias naturales y las ciencias sociales buscan caracterizar los sistemas físicos y los sistemas sociales, respectivamente, utilizando métodos empíricos, las ciencias formales son herramientas del lenguaje que se ocupan de caracterizar estructuras abstractas descritas por sistemas simbólicos. Las ciencias formales ayudan a las ciencias naturales y sociales proporcionando información sobre las estructuras utilizadas para describir el mundo físico y qué inferencias se pueden hacer sobre ellas.

Etimología

El uso moderno del término ciencias formales, en la literatura en idioma inglés, ocurre al menos ya en 1860, en una publicación póstuma de conferencias sobre filosofía de Sir William Hamilton en las que la lógica y las matemáticas se enumeran como ciencias formales. Remontándose aún más a 1819, Wilhelm Esser publicó un libro de texto en alemán sobre lógica, aclarando el significado de la designación ciencia formal (Formalwissenschaft) aplicada a la lógica; se proporciona una traducción al inglés en la conferencia de William Hamilton:

La lógica obtiene así, en el lenguaje común, el apelativo de ciencia formal, no en el sentido de que la Lógica tuviera sólo una forma y no un objeto, sino simplemente porque la forma del pensamiento humano es el objeto de la Lógica; de modo que el título ciencia formal es propiamente sólo una expresión abreviada.

Historia

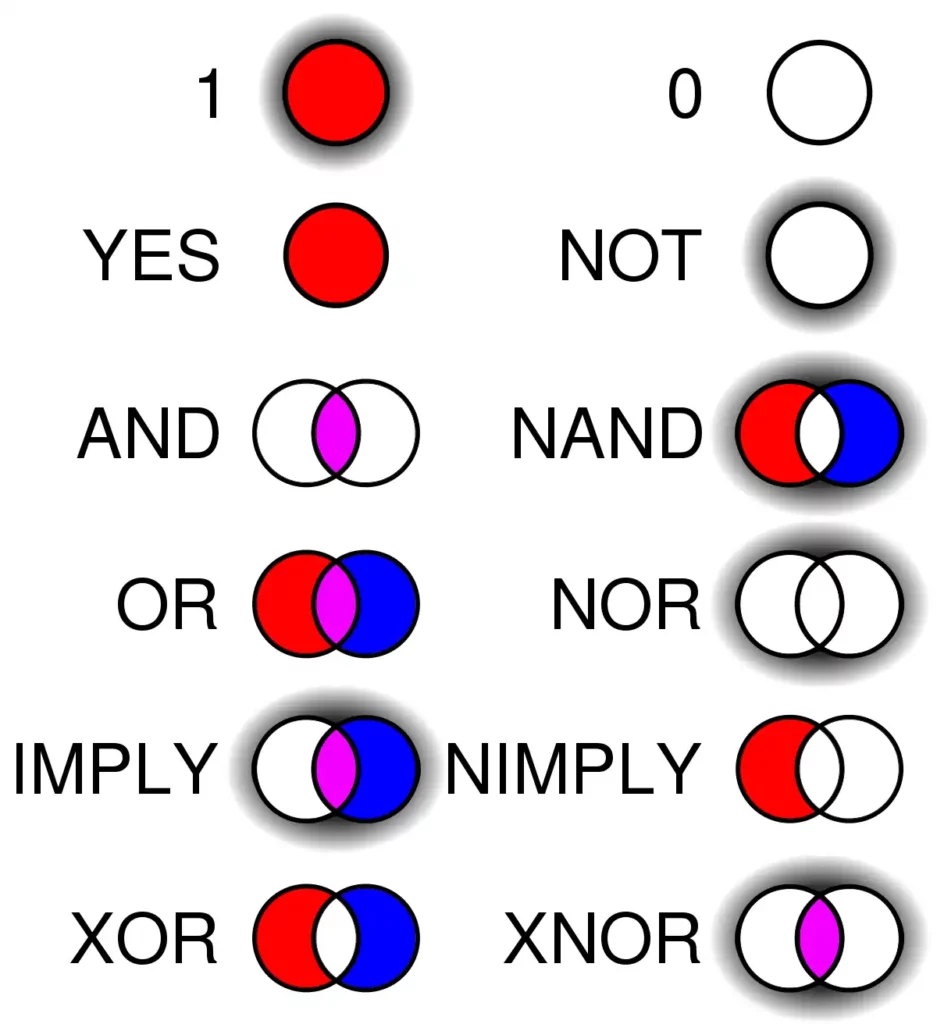
Las ciencias formales comenzaron antes de la formulación del método científico, con los textos matemáticos más antiguos que datan del 1800 a. C. (matemáticas babilónicas), 1600 a. C. (matemáticas egipcias) y 1000 a. C. (matemáticas indias). A partir de entonces diferentes culturas como la griega, la árabe y la persa hicieron importantes aportes a las matemáticas, mientras que la china y la japonesa, independientemente de culturas más lejanas, desarrollaron su propia tradición matemática.

Además de las matemáticas, la lógica es otro ejemplo de una de las materias más antiguas en el campo de las ciencias formales. Como análisis explícito de los métodos de razonamiento, la lógica recibió un desarrollo sostenido originalmente en tres lugares: India desde el siglo VI a. C., China en el siglo V a. C. y Grecia entre el siglo IV a. C. y el siglo I a. C.El tratamiento formalmente sofisticado de la lógica moderna desciende de la tradición griega, siendo informado de la transmisión de la lógica aristotélica, que luego fue desarrollada por los lógicos islámicos. La tradición india también continuó en el período moderno temprano. La tradición china nativa no sobrevivió más allá de la antigüedad, aunque la lógica india se adoptó más tarde en la China medieval.

Como una serie de otras disciplinas de la ciencia formal se basan en gran medida en las matemáticas, no existieron hasta que las matemáticas se desarrollaron en un nivel relativamente avanzado. Pierre de Fermat y Blaise Pascal (1654) y Christiaan Huygens (1657) iniciaron el primer estudio de la teoría de la probabilidad. A principios del siglo XIX, Gauss y Laplace desarrollaron la teoría matemática de la estadística, que también explicaba el uso de la estadística en seguros y contabilidad gubernamental. La estadística matemática fue reconocida como una disciplina matemática a principios del siglo XX.

A mediados del siglo XX, las matemáticas se ampliaron y enriquecieron con el surgimiento de nuevas ciencias matemáticas y disciplinas de ingeniería, como la investigación de operaciones y la ingeniería de sistemas. Estas ciencias se beneficiaron de la investigación básica en ingeniería eléctrica y luego del desarrollo de la computación eléctrica, que también estimuló la teoría de la información, el análisis numérico (computación científica) y la informática teórica. La informática teórica también se beneficia de la disciplina de la lógica matemática, que incluía la teoría de la computación.

Sucursales

Las ramas de la ciencia formal incluyen informática, matemáticas, estadística, ciencia de la información y ciencia de sistemas.

Diferencias con otras ciencias

Una de las razones por las que las matemáticas gozan de especial estima, por encima de todas las demás ciencias, es que sus leyes son absolutamente ciertas e indiscutibles, mientras que las de otras ciencias son hasta cierto punto discutibles y están en constante peligro de ser derrocadas por hechos recién descubiertos.—Alberto  Einstein

A diferencia de las ciencias empíricas (naturales y sociales), las ciencias formales no involucran procedimientos empíricos. Tampoco presuponen el conocimiento de hechos contingentes, ni describen el mundo real. En este sentido, las ciencias formales son tanto lógica como metodológicamente a priori, pues su contenido y validez son independientes de cualquier procedimiento empírico.

Por tanto, hablando con franqueza, la ciencia formal no es una ciencia empírica. Es un sistema lógico formal con su contenido dirigido a los componentes de la realidad experiencial, como la información y los pensamientos. Como señaló Francis Bacon en el siglo XVII, la verificación experimental de las proposiciones debe llevarse a cabo con rigurosidad y no puede tomarse la lógica misma como la forma de sacar conclusiones en la naturaleza. La ciencia formal es un método que ayuda a la ciencia empírica pero que no puede reemplazar a la ciencia empírica.

Si bien las ciencias formales son sistemas conceptuales, carentes de contenido empírico, esto no significa que no tengan relación con el mundo real. Pero esta relación es tal que sus enunciados formales son válidos en todos los mundos posibles concebibles, mientras que los enunciados basados ​​en teorías empíricas, como, por ejemplo, la relatividad general o la biología evolutiva, no son válidos en todos los mundos posibles y, eventualmente, pueden resultar no serlo. mantener en este mundo también. Por eso las ciencias formales son aplicables en todos los dominios y útiles en todas las ciencias empíricas.

Debido a su naturaleza no empírica, las ciencias formales se construyen delineando un conjunto de axiomas y definiciones a partir de los cuales se deducen otros enunciados (teoremas). Por ello, en la concepción lógico-positivista de la epistemología de la ciencia de Rudolf Carnap, se entiende que las teorías pertenecientes a las ciencias formales no contienen enunciados sintéticos, sino que todos sus enunciados son analíticos.