Catenoide

format_list_bulleted Contenido keyboard_arrow_down
ImprimirCitar
Surface of revolution of a catenary
three-dimensional diagram of a catenoid
Un catenoide
animation of a catenary sweeping out the shape of a catenoid as it rotates about a central point
Un catenoide obtenido de la rotación de un catenario

En geometría, una catenoide es un tipo de superficie que surge al girar una curva catenaria alrededor de un eje (una superficie de revolución). Es una superficie mínima, lo que significa que ocupa la menor área cuando está delimitada por un espacio cerrado. Fue descrito formalmente en 1744 por el matemático Leonhard Euler.

La película de jabón adherida a los anillos circulares gemelos tomará la forma de una catenoide. Debido a que son miembros de la misma familia asociada de superficies, un catenoide puede doblarse en una porción de un helicoide y viceversa.

Geometría

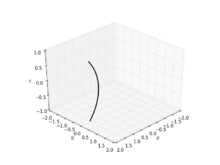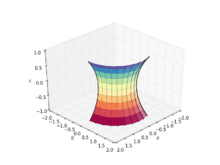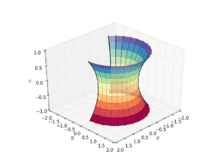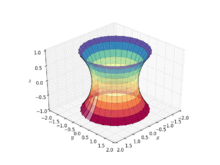
La catenoide fue la primera superficie mínima no trivial en el espacio euclidiano tridimensional que se descubrió aparte del plano. La catenoide se obtiene haciendo girar una catenaria alrededor de su directriz. Fue encontrado y resultó ser mínimo por Leonhard Euler en 1744.

Los primeros trabajos sobre el tema también fueron publicados por Jean Baptiste Meusnier. Sólo hay dos superficies mínimas de revolución (superficies de revolución que también son superficies mínimas): el plano y la catenoide.

La catenoide puede definirse mediante las siguientes ecuaciones paramétricas:

x=ccosh⁡ ⁡ vc#⁡ ⁡ uSí.=ccosh⁡ ⁡ vcpecado⁡ ⁡ uz=v{displaystyle {begin{aligned}x limit=ccosh {frac}cos} U\\ycccccH00\ {v}{c}sin U\z=vend{aligned}

Donde u▪ ▪ [− − π π ,π π ){displaystyle uin [-pipi]} y v▪ ▪ R{displaystyle vin mathbb {R} y c{displaystyle c} es una constante no cero real.

En coordenadas cilíndricas:

*** *** =ccosh⁡ ⁡ zc,{displaystyle rho =ccosh {frac {Z}{c},}

Donde c{displaystyle c} es una constante real.

Se puede formar un modelo físico de un catenoide sumergiendo dos anillos circulares en una solución jabonosa y separando lentamente los círculos.

La catenoide también se puede definir aproximadamente mediante el método de cuadrícula estirada como un modelo 3D de facetas.

Transformación helicoidal

Continuous animation showing a helicoid deforming into a catenoid and back to a helicoid
Deformación de un helicoide en un catenoide

Debido a que son miembros de la misma familia asociada de superficies, se puede doblar una catenoide en una porción de una helicoide sin estirarla. En otras palabras, se puede hacer una deformación (principalmente) continua e isométrica de una catenoide a una parte del helicoide de modo que cada miembro de la familia de deformación sea mínimo (con una curvatura media de cero). Una parametrización de tal deformación viene dada por el sistema

x()u,v)=#⁡ ⁡ Silencio Silencio pecado⁡ ⁡ vpecado⁡ ⁡ u+pecado⁡ ⁡ Silencio Silencio cosh⁡ ⁡ v#⁡ ⁡ uSí.()u,v)=− − #⁡ ⁡ Silencio Silencio pecado⁡ ⁡ v#⁡ ⁡ u+pecado⁡ ⁡ Silencio Silencio cosh⁡ ⁡ vpecado⁡ ⁡ uz()u,v)=u#⁡ ⁡ Silencio Silencio +vpecado⁡ ⁡ Silencio Silencio {displaystyle {begin{aligned}x(u,v) limit=cos theta ,sinh v,sin u+theta ,cosh v,cos uy(u,v) limit=-cos theta ,sinh v,cos u+thetaigntheta,esush

para ()u,v)▪ ▪ ()− − π π ,π π ]× × ()− − JUEGO JUEGO ,JUEGO JUEGO ){displaystyle (u,v)in (-pipi]times (-inftyinfty)}, con parámetro de deformación <math alttext="{displaystyle -pi − − π π .Silencio Silencio ≤ ≤ π π {displaystyle -pi }<img alt="-pi , donde:

  • Silencio Silencio =π π {displaystyle theta =pi} corresponde a un helicoide de mano derecha,
  • Silencio Silencio =± ± π π /2{displaystyle theta =pm pi /2} corresponde a un catenoide, y
  • Silencio Silencio =0{displaystyle theta =0} corresponde a un helicoide zurdo.