Bloqueo de marea

El bloqueo de mareas resulta en la Luna girando alrededor de su eje en aproximadamente el mismo tiempo que se necesita para orbitar la Tierra. Excepto por la libración, esto resulta en la Luna manteniendo la misma cara girada hacia la Tierra, como se ve en la figura izquierda. La Luna se muestra en la vista polar, y no se dibuja a escala. Si la Luna no girara en absoluto, alternaría mostrar sus lados cercanos y lejanos a la Tierra, mientras se mueve alrededor de la Tierra en órbita, como se muestra en la figura correcta.

Vista lateral del sistema Plutón-Charon. Plutón y Charon se bloquean el uno al otro. Charon es lo suficientemente grande que el baricentro del sistema de Plutón está fuera de Plutón; por lo tanto, Plutón y Charon a veces se consideran un sistema binario.

El bloqueo de marea entre un par de cuerpos astronómicos en órbita conjunta se produce cuando uno de los objetos alcanza un estado en el que ya no hay ningún cambio neto en su tasa de rotación en el transcurso de una órbita completa. En el caso de que un cuerpo bloqueado por marea posea una rotación síncrona, el objeto tarda tanto en girar alrededor de su propio eje como en girar alrededor de su compañero. Por ejemplo, el mismo lado de la Luna siempre mira hacia la Tierra, aunque existe cierta variabilidad porque la órbita de la Luna no es perfectamente circular. Por lo general, solo el satélite está sincronizado por marea con el cuerpo más grande. Sin embargo, si tanto la diferencia de masa entre los dos cuerpos como la distancia entre ellos son relativamente pequeñas, cada uno puede estar bloqueado por las mareas entre sí; este es el caso de Plutón y Caronte, así como de Eris y Dysnomia. Los nombres alternativos para el proceso de bloqueo de marea son bloqueo gravitacional, rotación capturada y bloqueo de giro-órbita.

El efecto surge entre dos cuerpos cuando su interacción gravitacional ralentiza la rotación de un cuerpo hasta que se bloquea por marea. Durante muchos millones de años, las fuerzas de interacción cambian sus órbitas y velocidades de rotación como resultado del intercambio de energía y la disipación de calor. Cuando uno de los cuerpos alcanza un estado en el que ya no hay ningún cambio neto en su velocidad de rotación a lo largo de una órbita completa, se dice que está bloqueado por mareas. El objeto tiende a permanecer en este estado porque dejarlo requeriría agregar energía nuevamente al sistema. La órbita del objeto puede migrar con el tiempo para deshacer el bloqueo de marea, por ejemplo, si un planeta gigante perturba el objeto.

No todos los casos de bloqueo de marea implican una rotación síncrona. Con Mercurio, por ejemplo, este planeta bloqueado por mareas completa tres rotaciones por cada dos revoluciones alrededor del Sol, una resonancia de rotación-órbita de 3:2. En el caso especial en el que una órbita es casi circular y el eje de rotación del cuerpo no está significativamente inclinado, como la Luna, el bloqueo de marea da como resultado que el mismo hemisferio del objeto giratorio esté constantemente mirando a su compañero. Sin embargo, en este caso, la misma parte exacta del cuerpo no siempre mira a la pareja en todas las órbitas. Puede haber algunos cambios debido a variaciones en la velocidad orbital del cuerpo bloqueado y la inclinación de su eje de rotación.

Mecanismo

Si los bultos de marea en un cuerpo (verde) son mal alineados con el eje mayor (rojo), las fuerzas de marea (azul) ejercen un par neto en ese cuerpo que gira el cuerpo hacia la dirección del realineamiento.

Considere un par de objetos que coorbitan, A y B. El cambio en la velocidad de rotación necesaria para bloquear por marea el cuerpo B con el cuerpo más grande A es causado por el par aplicado por la gravedad de A sobre las protuberancias que ha inducido. en B por las fuerzas de marea.

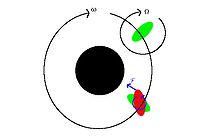
La fuerza gravitacional del objeto A sobre B variará con la distancia, siendo mayor en la superficie más cercana a A y menor en la más distante. Esto crea un gradiente gravitatorio a través del objeto B que distorsionará ligeramente su forma de equilibrio. El cuerpo del objeto B se alargará a lo largo del eje orientado hacia A y, a la inversa, se reducirá ligeramente en dimensión en direcciones ortogonales a este eje. Las distorsiones alargadas se conocen como protuberancias de marea. (Para la Tierra sólida, estas protuberancias pueden alcanzar desplazamientos de hasta alrededor de 0,4 m o 1 ft 4 in.) Cuando B aún no está bloqueada por mareas, las protuberancias viajan sobre su superficie debido a los movimientos orbitales, con uno de los dos &# 34;alto" protuberancias de marea que viajan cerca del punto donde el cuerpo A está arriba. Para grandes cuerpos astronómicos que son casi esféricos debido a la autogravitación, la distorsión de marea produce un esferoide ligeramente alargado, es decir, un elipsoide axialmente simétrico que se alarga a lo largo de su eje mayor. Los cuerpos más pequeños también experimentan distorsión, pero esta distorsión es menos regular.

El material de B ejerce resistencia a esta remodelación periódica causada por la fuerza de marea. En efecto, se requiere algo de tiempo para remodelar B a la forma de equilibrio gravitacional, momento en el cual las protuberancias en formación ya se han alejado una cierta distancia del eje A-B por la rotación de B. Vistos desde un punto ventajoso en el espacio, los puntos de máxima extensión de la protuberancia se desplazan del eje orientado hacia A. Si el período de rotación de B es más corto que su período orbital, las protuberancias se desplazan hacia delante del eje orientado hacia A en la dirección de rotación, mientras que si el período de rotación de B es más largo, las protuberancias se quedan atrás.

Debido a que las protuberancias ahora están desplazadas del eje A–B, la atracción gravitacional de A sobre la masa en ellas ejerce un par sobre B. La torsión sobre la protuberancia que mira hacia A actúa para atraer a B rotación en línea con su período orbital, mientras que el "atrás" protuberancia, que se aleja de A, actúa en el sentido opuesto. Sin embargo, la protuberancia en el lado que mira hacia A está más cerca de A que la protuberancia trasera por una distancia de aproximadamente el diámetro de B, y por lo tanto experimenta una fuerza gravitatoria y un par ligeramente más fuertes. El par neto resultante de ambas protuberancias siempre está en la dirección que actúa para sincronizar la rotación de B con su período orbital, lo que finalmente conduce al bloqueo de marea.

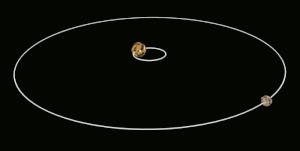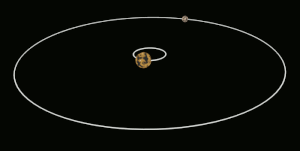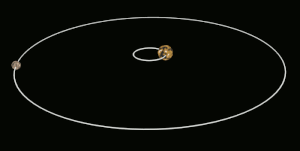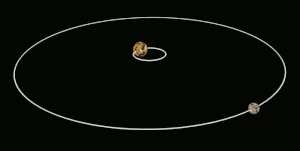
Cambios orbitales

En (1), un satélite orbita en la misma dirección que (pero más lento que) la rotación de su cuerpo padre. La bala de marea más cercana (rojo) atrae al satélite más que la bala más lejana (azul), ralentizando la rotación del padre mientras imparte una fuerza positiva neta (flechas dotadas que muestran fuerzas resueltas en sus componentes) en la dirección de la órbita, elevandola a una órbita superior (aceleración cerebral).
En (2) con la rotación invertida, la fuerza neta se opone a la dirección de órbita del satélite, bajando (desaceleración cerebral).

Si la frecuencia de rotación es mayor que la frecuencia orbital, surge una pequeña torque que contrarresta la rotación, bloqueando eventualmente las frecuencias (situación representada en verde)

El momento angular de todo el sistema A–B se conserva en este proceso, de modo que cuando B se ralentiza y pierde el momento angular de rotación, su momento angular orbital aumenta en una cantidad similar (hay también hay algunos efectos menores en la rotación de A). Esto da como resultado un aumento de la órbita de B alrededor de A junto con su desaceleración rotacional. Para el otro caso en el que B comienza a girar demasiado lentamente, el bloqueo de marea acelera su rotación y reduce su órbita.

Bloqueo del cuerpo más grande

El efecto de bloqueo de marea también lo experimenta el cuerpo más grande A, pero a un ritmo más lento porque el efecto gravitatorio de B es más débil debido a la masa más pequeña de B. Por ejemplo, la Luna está desacelerando gradualmente la rotación de la Tierra, en una cantidad que se vuelve perceptible a lo largo del tiempo geológico, como se revela en el registro fósil. Las estimaciones actuales son que esto (junto con la influencia de las mareas del Sol) ha ayudado a alargar el día de la Tierra de unas 6 horas a las 24 horas actuales (más de ≈ ⁠4½ mil millones de años). Actualmente, los relojes atómicos muestran que el día de la Tierra se alarga, en promedio, alrededor de 2,3 milisegundos por siglo. Con suficiente tiempo, esto crearía un bloqueo de marea mutuo entre la Tierra y la Luna. La duración del día de la Tierra aumentaría y la duración de un mes lunar también aumentaría. El día sideral de la Tierra eventualmente tendría la misma duración que el período orbital de la Luna, aproximadamente 47 veces la duración del día de la Tierra en la actualidad. Sin embargo, no se espera que la Tierra se bloquee por mareas con la Luna antes de que el Sol se convierta en una gigante roja y engulla a la Tierra y la Luna.

Para cuerpos de tamaño similar, el efecto puede ser de un tamaño comparable para ambos, y ambos pueden bloquearse entre sí en una escala de tiempo mucho más corta. Un ejemplo es el planeta enano Plutón y su satélite Caronte. Ya han llegado a un estado en el que Caronte es visible desde un solo hemisferio de Plutón y viceversa.

Órbitas excéntricas

Una comprensión errónea muy extendida es que un cuerpo tidally bloqueado gira permanentemente un lado a su anfitrión.

—Heller y otros (2011)

Para las órbitas que no tienen una excentricidad cercana a cero, la velocidad de rotación tiende a bloquearse con la velocidad orbital cuando el cuerpo está en el periápside, que es el punto de interacción de marea más fuerte entre los dos objetos. Si el objeto en órbita tiene un compañero, este tercer cuerpo puede hacer que la velocidad de rotación del objeto principal varíe de manera oscilatoria. Esta interacción también puede generar un aumento en la excentricidad orbital del objeto en órbita alrededor del primario, un efecto conocido como bombeo de excentricidad.

En algunos casos en los que la órbita es excéntrica y el efecto de marea es relativamente débil, el cuerpo más pequeño puede terminar en una llamada resonancia de órbita de espín, en lugar de estar bloqueada por mareas. Aquí, la relación entre el período de rotación de un cuerpo y su propio período orbital es una fracción simple diferente de 1:1. Un caso bien conocido es la rotación de Mercurio, que está bloqueado en su propia órbita alrededor del Sol en una resonancia de 3:2. Esto da como resultado que la velocidad de rotación coincida aproximadamente con la velocidad orbital alrededor del perihelio.

Se espera que muchos exoplanetas (especialmente los más cercanos) estén en resonancias de órbita de giro superiores a 1:1. Un planeta terrestre similar a Mercurio puede, por ejemplo, ser capturado en una resonancia de órbita de giro 3: 2, 2: 1 o 5: 2, con la probabilidad de que cada uno dependa de la excentricidad orbital.

Ocurrencia

Lunas

Debido al bloqueo de marea, los habitantes del cuerpo central nunca podrán ver la zona verde del satélite.

Las veinte lunas conocidas en el Sistema Solar que son lo suficientemente grandes para ser redondas están bloqueadas por mareas con sus primarias, porque orbitan muy cerca y la fuerza de las mareas aumenta rápidamente (como una función cúbica) con la distancia decreciente. Por otro lado, los satélites exteriores irregulares de los gigantes gaseosos (por ejemplo, Phoebe), que orbitan mucho más lejos que las grandes lunas conocidas, no están bloqueados por mareas.

Plutón y Caronte son un ejemplo extremo de bloqueo de marea. Caronte es una luna relativamente grande en comparación con su primaria y también tiene una órbita muy cercana. Esto da como resultado que Plutón y Caronte estén mutuamente bloqueados por mareas. Las otras lunas de Plutón no están bloqueadas por mareas; Styx, Nix, Kerberos e Hydra giran caóticamente debido a la influencia de Caronte. Del mismo modo, Eris y Dysnomia están mutuamente bloqueados por mareas.

La situación de bloqueo de mareas para las lunas de asteroides se desconoce en gran medida, pero se espera que los binarios que orbitan cerca estén bloqueados por mareas, así como los binarios de contacto.

La Luna de la Tierra

La vibración causa variabilidad en la porción de la Luna visible desde la Tierra.

La rotación de la Luna de la Tierra y los períodos orbitales están bloqueados entre sí por mareas, por lo que no importa cuándo se observe la Luna desde la Tierra, siempre se ve el mismo hemisferio de la Luna. La mayor parte de la cara oculta de la Luna no se vio hasta 1959, cuando se transmitieron fotografías de la mayor parte de la cara oculta desde la nave espacial soviética Luna 3.

Cuando se observa la Tierra desde la Luna, la Tierra no parece moverse por el cielo. Permanece en el mismo lugar mostrando casi toda su superficie mientras gira sobre su eje.

A pesar de que los períodos rotacional y orbital de la Luna están exactamente bloqueados, alrededor del 59 por ciento de la superficie total de la Luna se puede ver con observaciones repetidas desde la Tierra, debido a los fenómenos de libración y paralaje. Las libraciones son causadas principalmente por la velocidad orbital variable de la Luna debido a la excentricidad de su órbita: esto permite que se vean hasta unos 6° más a lo largo de su perímetro desde la Tierra. El paralaje es un efecto geométrico: en la superficie de la Tierra, los observadores están desplazados de la línea que pasa por los centros de la Tierra y la Luna, y debido a esto, se puede ver alrededor de 1° más alrededor del lado de la Luna cuando está en el horizonte local.

Planetas

Durante algún tiempo se pensó que Mercurio estaba en rotación sincrónica con el Sol. Esto se debió a que siempre que Mercurio estaba mejor ubicado para la observación, el mismo lado miraba hacia adentro. Las observaciones de radar en 1965 demostraron, en cambio, que Mercurio tiene una resonancia de giro-órbita de 3: 2, girando tres veces por cada dos revoluciones alrededor del Sol, lo que da como resultado el mismo posicionamiento en esos puntos de observación. El modelado ha demostrado que Mercurio fue capturado en el estado de órbita de giro 3: 2 muy temprano en su historia, probablemente dentro de 10 a 20 millones de años después de su formación.

El intervalo de 583,92 días entre acercamientos sucesivos de Venus a la Tierra es igual a 5,001444 días solares venusianos, lo que hace que aproximadamente la misma cara sea visible desde la Tierra en cada acercamiento. Se desconoce si esta relación surgió por casualidad o es el resultado de algún tipo de bloqueo de marea con la Tierra.

El exoplaneta Próxima Centauri b, descubierto en 2016 y que orbita alrededor de Próxima Centauri, tiene un bloqueo de marea casi seguro, lo que expresa una rotación sincronizada o una resonancia de órbita de giro de 3:2 como la de Mercurio.

Una forma hipotética de exoplanetas bloqueados por mareas son los planetas del globo ocular, que a su vez se dividen en "calientes" y "frío" planetas globo ocular.

Estrellas

Se espera que las estrellas binarias cercanas en todo el universo estén bloqueadas por mareas entre sí, y también se cree que los planetas extrasolares que se ha descubierto que orbitan sus primarias extremadamente cerca también están bloqueados por mareas. Un ejemplo inusual, confirmado por MOST, puede ser Tau Boötis, una estrella que probablemente esté bloqueada por mareas por su planeta Tau Boötis b. Si es así, es casi seguro que el bloqueo de marea es mutuo.

Escala de tiempo

Se puede obtener una estimación del tiempo que tarda un cuerpo en bloquearse mediante la siguiente fórmula:

${displaystyle T_{text{lock}approx #frac {omega ¿Qué?$

dónde

• ${displaystyle omega ,}$ es la tasa de giro inicial expresada en radians por segundo,
• ${displaystyle a,}$ es el eje semi-major del movimiento del satélite alrededor del planeta (debido por el promedio de las distancias periapsis y apoapsis),
• ${displaystyle Yo...$ ${displaystyle approx 0.4;m_{2}$ es el momento de la inercia del satélite, donde ${displaystyle m_{s}$ es la masa del satélite y ${displaystyle R.$ es el radio medio del satélite,
• ${displaystyle Q,}$ es la función de disipación del satélite,
• ${displaystyle G,}$ es la constante gravitacional,
• ${displaystyle #$ es la masa del planeta (es decir, el objeto que se orbita), y
• ${displaystyle k_{2},}$ es el tidal Love número del satélite.

${displaystyle Q}$ y ${displaystyle K_{2}$ son generalmente muy poco conocidos excepto por la Luna, que ha ${displaystyle K_{2}/Q=0.0011}$. Para una estimación realmente difícil es común tomar ${displaystyle Qapprox 100}$ (tal vez conservadoramente, dando tiempos de bloqueo sobreestimados), y

${displaystyle {fnK}}}}$

dónde

• ${displaystyle rho ,}$ es la densidad del satélite
• ${displaystyle gapprox Gm_{s}/R^{2}$ es la gravedad superficial del satélite
• ${displaystyle mu ,}$ es la rigidez del satélite. Esto se puede tomar aproximadamente como 3×10¹⁰N·m⁻² para objetos rocosos y 4×10⁹N·m⁻² para helados.

Incluso sabiendo el tamaño y la densidad del satélite deja muchos parámetros que deben ser estimados (especialmente ⋅, Q, y μ), para que cualquier tiempo calculado de bloqueo obtenido sea inexacto, incluso a factores de diez. Además, durante la fase de bloqueo de marea el eje semi-major ${displaystyle a}$ puede haber sido significativamente diferente de lo observado hoy en día debido a la aceleración posterior de la marea, y el tiempo de bloqueo es extremadamente sensible a este valor.

Debido a que la incertidumbre es tan alta, las fórmulas anteriores se pueden simplificar para dar un poco menos engorroso. Suponiendo que el satélite sea esférico, ${displaystyle k_{2}ll 1,Q=100}$, y es razonable adivinar una revolución cada 12 horas en el estado inicial no bloqueado (la mayoría de los asteroides tienen períodos de rotación entre aproximadamente 2 horas y aproximadamente 2 días)

${displaystyle T_{text{lock}approx 6 {fnMicroc {6}Rmu} {fnMicrosoft Sans Serif}$

con masas en kilos, distancias en metros, y ${displaystyle mu }$ en newtons por metro cuadrado; ${displaystyle mu }$ puede ser tomada aproximadamente como 3×10¹⁰N·m⁻² para objetos rocosos y 4×10⁹N·m⁻² para helados.

Hay una dependencia extremadamente fuerte del eje semi-major ${displaystyle a}$.

Para vincular un cuerpo principal a su satélite, como en el caso de Plutón, se pueden intercambiar los parámetros del satélite y del cuerpo principal.

Una conclusión es que, otras cosas siendo iguales (como ${displaystyle Q}$ y ${displaystyle mu }$), una luna grande se bloqueará más rápido que una luna más pequeña a la misma distancia orbital del planeta porque ${displaystyle #$ crece como el cubo del radio satelital ${displaystyle R.$. Un posible ejemplo de esto es en el sistema Saturno, donde Hyperion no está tidally bloqueado, mientras que el Iapetus más grande, que orbita a una mayor distancia, es. Sin embargo, esto no es claro porque Hyperion también experimenta fuerte conducción desde el Titan cercano, lo que obliga a su rotación a ser caótico.

Las fórmulas anteriores para la escala de tiempo del bloqueo pueden estar fuera por órdenes de magnitud, porque ignoran la dependencia de frecuencias ${displaystyle K_{2}/Q}$. Más importante aún, pueden ser inaplicables a los binarios viscosos (estrellas dobles, o asteroides dobles que son escombros), porque la dinámica de giro-orbito de tales cuerpos se define principalmente por su viscosidad, no rigidez.

Lista de cuerpos bloqueados por mareas conocidos

Sistema Solar

Extrasolar

• Los métodos de detección más exitosos de exoplanetas (transits y velocidades radiales) sufren de un sesgo observacional claro que favorece la detección de planetas cerca de la estrella; por lo tanto, el 85% de los exoplanetas detectados están dentro de la zona de bloqueo de marea, lo que hace difícil estimar la verdadera incidencia de este fenómeno. Tau Boötis es conocido por estar encerrado en el planeta gigante cercano Tau Boötis b.

Es probable que los cuerpos estén encerrados

Sistema Solar

En base a la comparación entre el tiempo probable necesario para fijar un cuerpo a su principal y el tiempo que ha estado en su órbita actual (comparable con la edad del Sistema Solar para la mayoría de las lunas planetarias), se cree que varias lunas para ser bloqueado. Sin embargo, sus rotaciones no se conocen o no se conocen lo suficiente. Estos son:

Probablemente fijado a Saturno

Probablemente bloqueado en Urano

Probablemente bloqueada a Neptuno

Extrasolares

• Gliese 581c, Gliese 581g, Gliese 581b, y Gliese 581e pueden estar tidally encerrados a su estrella padre Gliese 581. Gliese 581d es casi sin duda capturado ya sea en la 2:1 o en la resonancia 3,2 spin-orbit con la misma estrella.
• Es probable que todos los planetas del sistema TRAPPIST-1 estén bloqueados.