Azimut
Un acimut (del árabe: اَلسُّمُوت, romanizado: as-sumūt, lit. 'las direcciones') es una medida angular en un sistema de coordenadas esféricas. Más específicamente, es el ángulo horizontal desde una dirección cardinal, más comúnmente hacia el norte.
Matemáticamente, el vector de posición relativa desde un observador (origen) hasta un punto de interés se proyecta perpendicularmente sobre un plano de referencia (el plano horizontal); el ángulo entre el vector proyectado y un vector de referencia en el plano de referencia se denomina acimut.
Cuando se usa como coordenada celeste, el acimut es la dirección horizontal de una estrella u otro objeto astronómico en el cielo. La estrella es el punto de interés, el plano de referencia es el área local (por ejemplo, un área circular con un radio de 5 km al nivel del mar) alrededor de un observador en la superficie de la Tierra y el vector de referencia apunta al norte verdadero. El acimut es el ángulo entre el vector norte y el vector de la estrella en el plano horizontal.
El acimut generalmente se mide en grados (°). El concepto se utiliza en navegación, astronomía, ingeniería, cartografía, minería y balística.
Etimología
La palabra azimut se usa en todos los idiomas europeos en la actualidad. Tiene su origen en el árabe medieval السموت (al-sumūt, pronunciado as-sumūt), que significa "las direcciones" (plural del árabe السمت al-samt = "la dirección"). La palabra árabe entró en el latín medieval tardío en un contexto astronómico y, en particular, en el uso de la versión árabe del instrumento astronómico astrolabio. Su primer uso registrado en inglés es en la década de 1390 en el Tratado sobre el astrolabio de Geoffrey Chaucer. El primer registro conocido en cualquier idioma occidental está en español en la década de 1270 en un libro de astronomía que se derivó en gran parte de fuentes árabes, los Libros del saber de astronomía encargados por el rey Alfonso X de Castilla.
En astronomía
En el sistema de coordenadas horizontales, utilizado en la navegación celeste, el acimut es una de las dos coordenadas. El otro es altitud, a veces llamado elevación sobre el horizonte. También se utiliza para la instalación de antenas parabólicas (ver también: buscador de satélites). En la astronomía moderna, el azimut casi siempre se mide desde el norte.
En navegación
En la navegación terrestre, el azimut generalmente se denota alfa, α, y se define como un ángulo horizontal medido en el sentido de las agujas del reloj desde una línea base norte o meridiano. Acimut también se ha definido de manera más general como un ángulo horizontal medido en el sentido de las agujas del reloj desde cualquier plano de referencia fijo o línea de dirección base fácilmente establecida.
Hoy en día, el plano de referencia para un acimut suele ser el norte verdadero, medido como un acimut de 0°, aunque se pueden usar otras unidades angulares (grad, mil). Moviéndose en el sentido de las agujas del reloj en un círculo de 360 grados, el este tiene un acimut de 90°, el sur de 180° y el oeste de 270°. Hay excepciones: algunos sistemas de navegación utilizan el sur como vector de referencia. Cualquier dirección puede ser el vector de referencia, siempre que esté claramente definida.
Con bastante frecuencia, los acimutes o las orientaciones de la brújula se establecen en un sistema en el que el norte o el sur pueden ser el cero, y el ángulo puede medirse en sentido horario o antihorario desde el cero. Por ejemplo, un rumbo podría describirse como "(desde) el sur, (girar) treinta grados (hacia el) este" (las palabras entre paréntesis generalmente se omiten), abreviado "S30°E", que es el rumbo de 30 grados en dirección este desde el sur, es decir, el rumbo de 150 grados en el sentido de las agujas del reloj desde el norte. La dirección de referencia, indicada en primer lugar, siempre es norte o sur, y la dirección de giro, indicada en último lugar, es este u oeste. Las direcciones se eligen de modo que el ángulo, establecido entre ellas, sea positivo, entre cero y 90 grados. Si el rumbo está exactamente en la dirección de uno de los puntos cardinales, una notación diferente, p. En su lugar, se utiliza "hacia el este".
Acimutes verdaderos basados en el norte
| Dirección | Azimuth |
|---|---|
| Norte | 0° |
| Nordeste | 22,5° |
| Nordeste | 45° |
| East-northeast | 67,5° |
| Oriental | 90° |
| East-southeast | 112,5° |
| Sureste | 135° |
| Sureste | 157,5° |
| Dirección | Azimuth |
|---|---|
| Sur | 180° |
| Sudoeste | 202.5° |
| Sudoeste | 225° |
| West-southwest | 247,5° |
| Oeste | 270° |
| West-northwest | 292.5° |
| Noroeste | 315° |
| Noroeste | 337,5° |
En geodesia
Estamos de pie en la latitud φ φ 1{displaystyle varphi _{1}, longitud cero; queremos encontrar el azimut desde nuestro punto de vista hasta el punto 2 en latitud φ φ 2{displaystyle varphi _{2}, longitud L (positivo hacia el este). Podemos conseguir una aproximación justa asumiendo que la Tierra es una esfera, en cuyo caso el azimut α es dado por
- # α α =pecado L# φ φ 1# φ φ 2− − pecado φ φ 1# L{displaystyle tan alpha ={frac {sin L}{cos varphi _{1}tan varphi ¿Por qué?
Una mejor aproximación supone que la Tierra es una esfera ligeramente aplastada (un esferoide achatado); azimut entonces tiene al menos dos significados ligeramente diferentes. Acimut de sección normal es el ángulo medido en nuestro punto de vista por un teodolito cuyo eje es perpendicular a la superficie del esferoide; El azimut geodésico (o azimut geodésico) es el ángulo entre el norte y la geodésica elipsoidal (el camino más corto en la superficie del esferoide desde nuestro punto de vista hasta el Punto 2). La diferencia suele ser insignificante: menos de 0,03 segundos de arco para distancias inferiores a 100 km.
El acimut de la sección normal se puede calcular de la siguiente manera:
- e2=f()2− − f)1− − e2=()1− − f)2▪ ▪ =()1− − e2)# φ φ 2# φ φ 1+e21+()1− − e2)()# φ φ 2)21+()1− − e2)()# φ φ 1)2# α α =pecado L()▪ ▪ − − # L)pecado φ φ 1{fnMicrosoft Sans Serif}1-e^{2}1-e^{2} {2-f)}\Lambda=left] (1-e^{2}right){frac {tan varphi {2}{tan varphi - ¿Por qué? ¿Qué?
donde f es el aplanamiento y e la excentricidad del esferoide elegido (por ejemplo, 1⁄298.257223563 para WGS84). Si φ1 = 0 entonces
- # α α =pecado L()1− − e2)# φ φ 2{displaystyle tan alpha # {frac {sin L}{left(1-e^{2}right)tan varphi ¿Qué?
Para calcular el azimut del sol o de una estrella dada su declinación y ángulo horario en nuestra ubicación, modificamos la fórmula de una tierra esférica. Reemplace φ2 con la declinación y la diferencia de longitud con el ángulo horario, y cambie el signo (ya que el ángulo horario es positivo hacia el oeste en lugar del este).
En cartografía
El azimut cartográfico o azimut de cuadrícula (en grados decimales) se puede calcular cuando se conocen las coordenadas de 2 puntos en un plano (coordenadas cartográficas):
- α α =180π π atan2 ()X2− − X1,Y2− − Y1){displaystyle alpha = {180}{pi} - ¿Qué?
Tenga en cuenta que los ejes de referencia se intercambian en relación con el sistema matemático de coordenadas polares (en sentido contrario a las agujas del reloj) y que el acimut es en el sentido de las agujas del reloj en relación con el norte. Esta es la razón por la que se intercambian los ejes X e Y en la fórmula anterior. Si el acimut se vuelve negativo, siempre se pueden sumar 360°.
La fórmula en radianes sería un poco más fácil:
- α α =atan2 ()X2− − X1,Y2− − Y1){displaystyle alpha =operatorname {atan2} (X_{2}-X_{1},Y_{2}-Y_{1}}
Note el cambio ()x,Sí.){displaystyle (x,y)} en contraste con lo normal ()Sí.,x){displaystyle (y,x)} orden de entrada atan2.
El problema opuesto ocurre cuando las coordenadas (X1, Y1) de un punto, el distancia D, y el acimut α a otro punto (X2, Y 2) son conocidas, se pueden calcular sus coordenadas:
- X2=X1+Dpecado α α Y2=Y1+D# α α {displaystyle {begin{aligned}X_{2} \Y_{2}=Y_{1}+Dcos alpha end{aligned}}
Esto se usa normalmente en triangulación e identificación de azimut (AzID), especialmente en aplicaciones de radar.
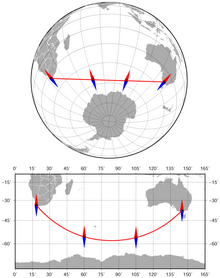
Proyecciones de mapas
Existe una amplia variedad de proyecciones cartográficas azimutales. Todos ellos tienen la propiedad de que se conservan las direcciones (los acimutes) desde un punto central. Algunos sistemas de navegación utilizan el sur como plano de referencia. Sin embargo, cualquier dirección puede servir como plano de referencia, siempre que esté claramente definida para todos los que utilicen ese sistema.
Coordenadas relacionadas
Ascensión recta
Si, en lugar de medir desde y a lo largo del horizonte, los ángulos se miden desde y a lo largo del ecuador celeste, los ángulos se denominan ascensión recta si se refieren al equinoccio vernal, o ángulo horario si se refieren al meridiano celeste.
Coordenada polar
En matemáticas, el ángulo acimutal de un punto en coordenadas cilíndricas o esféricas es el ángulo en sentido contrario a las agujas del reloj entre el eje positivo x y la proyección del vector sobre el xy-plano. El ángulo es el mismo que un ángulo en coordenadas polares de la componente del vector en el plano xy y normalmente se mide en radianes en lugar de grados. Además de medir el ángulo de manera diferente, en aplicaciones matemáticas, theta, θ, se usa muy a menudo para representar el acimut en lugar de la representación del símbolo phi φ.
Otros usos
Para las unidades de cinta magnética, azimut se refiere al ángulo entre los cabezales de la cinta y la cinta.
En la literatura y los experimentos de localización de sonido, el azimut se refiere al ángulo que forma la fuente de sonido en comparación con la línea recta imaginaria que se dibuja desde el interior de la cabeza a través del área entre los ojos.
Un propulsor azimutal en la construcción naval es una hélice que se puede girar horizontalmente.
Contenido relacionado
Aeropuerto Internacional Luis Muñoz Marín
Río Orontes
Jean-Baptiste Biot