Argumento del cubo

El argumento del cubo giratorio de Isaac Newton (también conocido como cubo de Newton) fue diseñado para demostrar que el verdadero movimiento de rotación no se puede definir como el rotación relativa del cuerpo con respecto a los cuerpos inmediatamente circundantes. Es uno de los cinco argumentos de las "propiedades, causas y efectos" de "movimiento y reposo verdaderos" que respaldan su afirmación de que, en general, el movimiento y el reposo verdaderos no pueden definirse como instancias especiales de movimiento o reposo en relación con otros cuerpos, sino que pueden definirse solo por referencia al espacio absoluto. Alternativamente, estos experimentos proporcionan una definición operativa de lo que significa "rotación absoluta" y no pretenden abordar la cuestión de "rotación relativa a qué?&# 34; La relatividad general prescinde del espacio absoluto y de la física cuya causa es externa al sistema, con el concepto de geodésica del espacio-tiempo.

Antecedentes

Estos argumentos, y una discusión de las distinciones entre tiempo, espacio, lugar y movimiento absolutos y relativos, aparecen en un escolio al final de las secciones de Definiciones en el Libro I del trabajo de Newton, The Mathematical Principios de Filosofía Natural (1687) (que no debe confundirse con Escolio General al final del Libro III), que estableció los fundamentos de la mecánica clásica e introdujo su ley de gravitación universal, que produjo la primera explicación dinámica cuantitativamente adecuada del movimiento planetario.

A pesar de su adopción del principio de la inercia rectilínea y el reconocimiento de la relatividad cinemática del movimiento aparente (que subyace si el sistema ptolemaico o el copernicano son correctos), los filósofos naturales del siglo XVII continuaron considerando el movimiento y el reposo verdaderos como descriptores separados físicamente de un cuerpo individual. El punto de vista dominante al que se oponía Newton fue ideado por René Descartes y apoyado (en parte) por Gottfried Leibniz. Sostenía que el espacio vacío es una imposibilidad metafísica porque el espacio no es otra cosa que la extensión de la materia, o sea, que cuando se habla del espacio entre las cosas en realidad se está haciendo referencia a la relación que existe entre esas cosas y no a alguna entidad que se interpone entre ellos. De acuerdo con el entendimiento anterior, cualquier afirmación sobre el movimiento de un cuerpo se reduce a una descripción en el tiempo en la que el cuerpo bajo consideración se encuentra en t₁ cerca de un grupo de "punto de referencia" cuerpos y en algún t₂ se encuentra en las cercanías de algún otro "punto de referencia" cuerpo o cuerpos.

Detección de rotación: las banderas rojas aparecen en brazos flexibles cuando uno de los objetos realmente gira. R: El objeto central gira. B: El anillo exterior gira, pero en dirección opuesta. C: Ambos giran, pero en direcciones opuestas. D: Ambos están unidos y giran en la misma dirección.

Descartes reconoció que habría una diferencia real, sin embargo, entre una situación en la que un cuerpo con partes móviles y originalmente en reposo con respecto a un anillo circundante fuera acelerado a una cierta velocidad angular con respecto al anillo, y otra situación en la que el anillo circundante recibió una aceleración contraria con respecto al objeto central. Teniendo únicamente en cuenta el objeto central y el anillo que lo rodea, los movimientos serían indistinguibles entre sí suponiendo que tanto el objeto central como el anillo que lo rodea fueran objetos absolutamente rígidos. Sin embargo, si ni el objeto central ni el anillo circundante fueran absolutamente rígidos, las partes de uno o ambos tenderían a salirse del eje de rotación.

Por razones contingentes relacionadas con la Inquisición, Descartes habló del movimiento tanto como absoluto como relativo.

A finales del siglo XIX, se volvió a introducir la afirmación de que todo movimiento es relativo, especialmente por Ernst Mach (1883).

Cuando, en consecuencia, decimos que un cuerpo conserva sin cambios su dirección y velocidad en el espacio, nuestra afirmación no es nada más o menos que una referencia abreviada el universo entero.

—Ernst Mach; citado por Ciufolini y Wheeler: Gravitación e Inercia, pág. 387

El argumento

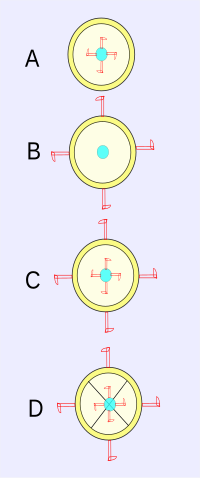
Newton habla de un balde (en latín: situla) lleno de agua que cuelga de una cuerda. Si la cuerda se retuerce con fuerza sobre sí misma y luego se suelta la cubeta, comienza a girar rápidamente, no solo con respecto al experimentador, sino también en relación con el agua que contiene. (Esta situación correspondería al diagrama B anterior).

Aunque el movimiento relativo en esta etapa es mayor, la superficie del agua permanece plana, lo que indica que las partes del agua no tienen tendencia a alejarse del eje del movimiento relativo, a pesar de la proximidad al balde. Eventualmente, a medida que la cuerda continúa desenrollándose, la superficie del agua asume una forma cóncava a medida que adquiere el movimiento del balde girando en relación con el experimentador. Esta forma cóncava muestra que el agua está girando, a pesar de que el agua está en reposo con respecto al balde. En otras palabras, no es el movimiento relativo del balde y el agua lo que causa la concavidad del agua, contrariamente a la idea de que los movimientos solo pueden ser relativos y que no hay movimiento absoluto. (Esta situación correspondería al diagrama D.) Posiblemente la concavidad del agua muestra una rotación relativa a algo más: ¿digamos espacio absoluto? Newton dice: "Uno puede encontrar y medir el movimiento circular verdadero y absoluto del agua".

En la traducción de Andrew Motte de 1846 de las palabras de Newton:

Si un vaso, colgado por un cordón largo, es tan a menudo girado que el cordón está fuertemente retorcido, luego lleno de agua, y mantenido en reposo junto con el agua; después, por la acción repentina de otra fuerza, se azota de la manera contraria, y mientras el cordón es intwisting sí mismo, el vaso continúa durante algún tiempo este movimiento; la superficie del agua será inicialmente lisa, como antes de que el vaso se mueve gradualmente; Esta ascensión del agua muestra su empeño en retroceder del eje de su movimiento; y el movimiento circular verdadero y absoluto del agua, que es directamente contrario al relativo, se descubre a sí mismo, y puede ser medido por este esfuerzo.... Y por lo tanto, este esfuerzo no depende de ninguna traducción del agua respecto a los cuerpos ambientales, ni puede definirse un movimiento circular verdadero por tal traducción...; pero los movimientos relativos... son totalmente desprovistos de cualquier efecto real.... De hecho, es una cuestión de gran dificultad descubrir, y efectivamente distinguir, los verdaderos movimientos de cuerpos particulares de lo aparente; porque las partes de ese espacio inamovible en el que se realizan estos movimientos, no vienen por ningún medio bajo las observaciones de nuestros sentidos.

—Isaac Newton; Principia, Libro 1: Scholium

El argumento de que el movimiento es absoluto, no relativo, es incompleto, ya que limita a los participantes relevantes para el experimento solo al balde y al agua, una limitación que no se ha establecido. De hecho, la concavidad del agua implica claramente atracción gravitacional y, por implicación, la Tierra también participa. Aquí hay una crítica debido a que Mach argumenta que solo se establece el movimiento relativo:

El experimento de Newton con el vaso rotatorio de agua simplemente nos informa que la rotación relativa del agua con respecto a los lados del vaso no produce fuerzas centrífugas notables, pero que tales fuerzas son producidas por sus rotaciones relativas con respecto a la masa de la tierra y otros cuerpos celestes.

—Ernst Mach, citado por L. Bouquiaux en Leibniz, pág. 104

El grado en que la hipótesis de Mach se integra en la relatividad general se analiza en el artículo El principio de Mach; generalmente se sostiene que la relatividad general no es enteramente machista.

Todos los observadores están de acuerdo en que la superficie del agua en rotación es curva. Sin embargo, la explicación de esta curvatura involucra la fuerza centrífuga para todos los observadores con la excepción de un observador verdaderamente estacionario, quien encuentra que la curvatura es consistente con la velocidad de rotación del agua mientras la observa, sin necesidad de una fuerza centrífuga adicional. Por lo tanto, se puede identificar un marco estacionario y no es necesario preguntar "Estacionario con respecto a qué?":

La pregunta original, "¿relativa a qué marco de referencia sostienen las leyes del movimiento?" se revela erróneamente planteada. Para las leyes del movimiento esencialmente determinar a class of reference frames, and (in principle) a procedure for constructing them.

Newton también propuso un experimento mental complementario con el mismo objetivo de determinar la ocurrencia de rotación absoluta: el ejemplo de observar dos esferas idénticas en rotación alrededor de su centro de gravedad y unidas por una cuerda. La aparición de tensión en la cuerda es indicativa de rotación absoluta; ver Esferas giratorias.

Análisis detallado

La interfaz de dos líquidos inmiscibles girando alrededor de un eje vertical es un paraboloide circular ascendente.

El interés histórico del experimento del balde giratorio es su utilidad al sugerir que se puede detectar la rotación absoluta mediante la observación de la forma de la superficie del agua. Sin embargo, uno podría preguntarse cómo la rotación provoca este cambio. A continuación se presentan dos enfoques para comprender la concavidad de la superficie del agua en rotación en un balde.

Esquema de fuerza para un elemento de superficie de agua en el marco co-rotante. Top: Sección radial y punto seleccionado sobre superficie de agua; el agua, el marco de corotación y la sección radial comparten una frecuencia angular constante de rotación dada por el vector Ω. Bottom: Diagrama de fuerza en el punto seleccionado sobre la superficie. La pendiente de la superficie se ajusta para hacer que las tres fuerzas suman cero.

Leyes del movimiento de Newton

La forma de la superficie de un líquido en rotación en un balde se puede determinar utilizando las leyes de Newton para las diversas fuerzas sobre un elemento de la superficie. Por ejemplo, véase Knudsen y Hjorth. El análisis comienza con el diagrama de cuerpo libre en el marco co-rotante donde el agua parece estacionaria. La altura del agua h = h(r) es una función de la distancia radial r desde el eje de rotación Ω, y el objetivo es determinar esta función. Se muestra que un elemento de volumen de agua en la superficie está sujeto a tres fuerzas: la fuerza vertical debida a la gravedad F_g, la fuerza centrífuga horizontal, radialmente hacia afuera F_Cfgl, y la fuerza normal a la superficie del agua F_n debida al resto del agua que rodea al seleccionado elemento de superficie. Se sabe que la fuerza debida al agua circundante es normal a la superficie del agua porque un líquido en equilibrio no puede soportar esfuerzos cortantes. Para citar a Anthony y Brackett:

La superficie de un fluido de densidad uniforme..., si en reposo, está en todas partes perpendicular a las líneas de fuerza; porque si esto no fuera así, la fuerza en un punto sobre la superficie podría resolverse en dos componentes, uno perpendicular y el otro tangente a la superficie. Pero por la naturaleza de un fluido, la fuerza tangencial establecería un movimiento del fluido, que es contrario a la afirmación de que el fluido está en reposo.

—William Arnold Anthony & Cyrus Fogg Brackett: Elementary Text-book of Physics, pág. 127

Además, debido a que el elemento agua no se mueve, la suma de las tres fuerzas debe ser cero. Para que sume cero, la fuerza del agua debe apuntar en dirección opuesta a la suma de las fuerzas centrífuga y de gravedad, lo que significa que la superficie del agua debe ajustarse para que sus puntos normales apunten en esta dirección. (Un problema muy similar es el diseño de un giro peraltado, donde la pendiente del giro se establece de modo que un automóvil no se salga de la carretera. La analogía en el caso de un balde giratorio es que el elemento de la superficie del agua "deslizarse hacia arriba o hacia abajo en la superficie a menos que la normal a la superficie se alinee con el vector resultante formado por la suma de vectores F_g + F_Cfgl.)

A medida que aumenta r, la fuerza centrífuga aumenta según la relación (las ecuaciones se escriben por unidad de masa):

FCfgl=mΩ Ω 2r,{displaystyle F_{mathrm Oh, Dios.

donde Ω es la velocidad constante de rotación del agua. La fuerza gravitacional no cambia en

Fg=mg,{displaystyle F_{mathrm {}=mg}

donde g es la aceleración de la gravedad. Estas dos fuerzas se suman para formar una resultante con un ángulo φ desde la vertical dada por

#⁡ ⁡ φ φ =FCfglFg=Ω Ω 2rg,{displaystyle tan varphi ={frac {F_{mathrm {Cfgl} {f}{mhm} {g} }={frac {fnK}}

que claramente aumenta a medida que aumenta r. Para asegurar que esta resultante sea normal a la superficie del agua y, por lo tanto, pueda ser anulada efectivamente por la fuerza del agua debajo, la normal a la superficie debe tener el mismo ángulo, es decir,

#⁡ ⁡ φ φ =dhdr,{displaystyle tan varphi ={frac {mathrm {d} h}{mathrm {d}.

lo que lleva a la ecuación diferencial ordinaria para la forma de la superficie:

dhdr=Ω Ω 2rg,{displaystyle {frac {mathrm} h}{mathrm {d} {fnMicroc} {fnK}}

o, integrando:

h()r)=h()0)+12g()Ω Ω r)2,{displaystyle h(r)=h(0)+{frac {1}{2g}left(Omega rright)^{2}}

donde h(0) es la altura del agua en r = 0. En otras palabras, la superficie del agua es parabólica en su dependencia del radio.

Energía potencial

La forma de la superficie del agua se puede encontrar de una manera diferente y muy intuitiva utilizando la interesante idea de la energía potencial asociada con la fuerza centrífuga en el marco co-rotatorio. En un marco de referencia que gira uniformemente a una velocidad angular Ω, la fuerza centrífuga ficticia es conservativa y tiene una energía potencial de la forma:

UCfgl=− − 12mΩ Ω 2r2,{displaystyle {fnK} {Cfgl}=-{frac} {1}{2}m Omega

donde r es el radio desde el eje de rotación. Este resultado se puede verificar tomando el gradiente del potencial para obtener la fuerza radialmente hacia afuera:

FCfgl=− − ∂ ∂ ∂ ∂ rUCfgl{displaystyle F_{mathrm {Cfgl}=-{frac {partial} }{partial {fnK} {fnK}} {fnK}} {fnK}}} {fn}}} {fn}} {fn}} {fn}} {fn}}}}} {fn}}} {\fn\fn\fnKfnKfn}}}}}}} {\\fnH}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\fn}\\\\\\\\\\\m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m {}}=mΩ Ω 2r.{displaystyle =mOmega ^{2}r}

El significado de la energía potencial (trabajo almacenado) es que el movimiento de un cuerpo de prueba de un radio más grande a un radio más pequeño implica realizar un trabajo contra la fuerza centrífuga y, por lo tanto, ganar energía potencial. Pero este cuerpo de prueba en el radio más pequeño donde su elevación es más baja ahora ha perdido energía potencial gravitatoria equivalente.

Por lo tanto, la energía potencial explica la concavidad de la superficie del agua en un cubo giratorio. Observe que en el equilibrio la superficie adopta una forma tal que un elemento de volumen en cualquier lugar de su superficie tiene la misma energía potencial que en cualquier otro. Siendo así, ningún elemento de agua en la superficie tiene ningún incentivo para cambiar de posición, porque todas las posiciones son equivalentes en energía. Es decir, se alcanza el equilibrio. Por otro lado, si estuvieran disponibles regiones superficiales con menor energía, el agua que ocupa lugares superficiales de mayor energía potencial se movería para ocupar estas posiciones de menor energía, ya que no existe una barrera para el movimiento lateral en un líquido ideal.

Podríamos imaginarnos alterando deliberadamente esta situación de equilibrio alterando momentáneamente de alguna manera la forma de la superficie del agua para que sea diferente de una superficie de igual energía. Este cambio de forma no sería estable, y el agua no permanecería en nuestra forma creada artificialmente, sino que participaría en una exploración transitoria de muchas formas hasta que se introdujeran fuerzas de fricción no ideales al chapotear, ya sea contra los lados del balde o por el agua. naturaleza no ideal del líquido, eliminó las oscilaciones y el agua se asentó hasta la forma de equilibrio.

Para ver el principio de una superficie de igual energía en funcionamiento, imagine aumentar gradualmente la velocidad de rotación del balde desde cero. La superficie del agua es plana al principio y claramente una superficie de igual energía potencial porque todos los puntos de la superficie están a la misma altura en el campo gravitacional que actúa sobre el agua. Sin embargo, a una pequeña velocidad angular de rotación, un elemento de agua superficial puede alcanzar una energía potencial más baja al moverse hacia afuera bajo la influencia de la fuerza centrífuga; Piense en un objeto que se mueve con la fuerza de la gravedad más cerca del centro de la tierra: el objeto reduce su energía potencial al cumplir con una fuerza. Debido a que el agua es incompresible y debe permanecer dentro de los límites de la cubeta, este movimiento hacia afuera aumenta la profundidad del agua en el radio más grande, aumentando la altura de la superficie en el radio más grande y reduciéndola en el radio más pequeño. La superficie del agua se vuelve ligeramente cóncava, con la consecuencia de que la energía potencial del agua en el radio mayor aumenta por el trabajo realizado contra la gravedad para alcanzar la mayor altura. A medida que aumenta la altura del agua, el movimiento hacia la periferia deja de ser ventajoso, porque la reducción de energía potencial por trabajar con la fuerza centrífuga se equilibra con el aumento de energía que trabaja contra la gravedad. Así, a una velocidad angular dada de rotación, una superficie cóncava representa la situación estable, y cuanto más rápida sea la rotación, más cóncava será esta superficie. Si se detiene la rotación, la energía almacenada en la formación de la superficie cóncava debe disiparse, por ejemplo, a través de la fricción, antes de que se restablezca una superficie plana en equilibrio.

Para implementar una superficie de energía potencial constante cuantitativamente, permita que la altura del agua sea h()r){displaystyle h(r),}: entonces la energía potencial por unidad masa contribuido por gravedad es gh()r){displaystyle gh(r)} y la energía potencial total por unidad de masa en la superficie

U=U0+gh()r)− − 12Ω Ω 2r2{displaystyle {U}={0}+gh(r)-{frac Omega ^{2}

con U0{displaystyle {fnK} el nivel de energía de fondo independiente de r. En una situación estática (sin movimiento del fluido en el marco giratorio), esta energía es constante independiente de la posición r. Requiriendo que la energía sea constante, obtenemos la forma parabólica:

h()r)=Ω Ω 22gr2+h()0),{displaystyle h(r)={frac {fnMicrosoft Sans Serif}

donde h(0) es la altura en r = 0 (el eje). Ver Figuras 1 y 2.

El principio de funcionamiento de la centrífuga también puede entenderse simplemente en términos de esta expresión para la energía potencial, que muestra que es energéticamente favorable cuando el volumen alejado del eje de rotación está ocupado por la sustancia más pesada.