Árbol (estructura de datos)

Este árbol sin surtido tiene valores no únicos y no binarios, ya que el número de niños varía de uno (por ejemplo, nodo 9) a tres (nodo 7). El nodo raíz, en la parte superior, no tiene padre.

En informática, un árbol es un tipo de datos abstractos ampliamente utilizado que representa una estructura de árbol jerárquico con un conjunto de nodos conectados. Cada nodo en el árbol se puede conectar a muchos hijos (según el tipo de árbol), pero debe estar conectado exactamente a un padre, excepto el nodo raíz, que no tiene padre. Estas restricciones significan que no hay ciclos o "bucles" (ningún nodo puede ser su propio ancestro), y también que cada hijo puede ser tratado como el nodo raíz de su propio subárbol, haciendo de la recursividad una técnica útil para atravesar árboles. A diferencia de las estructuras de datos lineales, muchos árboles no se pueden representar mediante relaciones entre nodos vecinos en una sola línea recta.

Los árboles binarios son un tipo de uso común, que restringen el número de hijos para cada padre a exactamente dos. Cuando se especifica el orden de los hijos, esta estructura de datos corresponde a un árbol ordenado en la teoría de grafos. Se puede asociar un valor o puntero a otros datos con cada nodo del árbol o, a veces, solo con los nodos de hoja, que no tienen hijos.

El tipo de datos abstracto se puede representar de varias maneras, incluida una lista de padres con punteros a hijos, una lista de hijos con punteros a padres o una lista de nodos y una lista separada de relaciones padre-hijo (un tipo específico de lista de adyacencia). Las representaciones también pueden ser más complicadas, por ejemplo, utilizando índices o listas de antepasados para el rendimiento.

Los árboles, tal como se usan en computación, son similares a las construcciones matemáticas de árboles en la teoría de grafos, árboles en la teoría de conjuntos y árboles en la teoría descriptiva de conjuntos, pero pueden ser diferentes.

Aplicaciones

Los árboles se usan comúnmente para representar o manipular datos jerárquicos en aplicaciones como:

• Sistemas de archivos para:
  • Estructura del directorio utilizada para organizar subdirectorios y archivos (los enlaces simbólicos crean gráficos no-árbol, como hacen múltiples enlaces duros al mismo archivo o directorio)
  • El mecanismo utilizado para asignar y vincular bloques de datos en el dispositivo de almacenamiento
• Jerarquía de clase o "árbol hereditario" mostrando las relaciones entre clases en programación orientada al objeto; la herencia múltiple produce gráficos no-árbol
• Abstract syntax trees for computer languages
• Tratamiento del lenguaje natural:
  • Árboles pares
  • Modelando pronunciamientos en una gramática generativa
  • Árbol de diálogo para generar conversaciones
• Modelos de Objetos de Documentos ("Árbol DOM") de documentos XML y HTML
• Buscar árboles almacenan datos de una manera que hace posible un algoritmo de búsqueda eficiente a través de traversal de árboles
  • Un árbol de búsqueda binaria es un tipo de árbol binario
• Representando listas ordenadas de datos
• Imagen generada por ordenador:
  • Partición espacial, incluyendo partición espacial binaria
  • Composicion digital
• Robando Barnes – Hut árboles solían simular galaxias
• Implementación de montones
• Sets anidados
• Taxonomías jerárquicas como la Clasificación Dewey Decimal con secciones de creciente especificidad.
• Memoria temporal jerárquica
• Programación genética
• agrupación jerárquica

Los árboles se pueden usar para representar y manipular varias estructuras matemáticas, como:

• Sendas a través de un gráfico arbitrario de nodos y bordes (incluidos varios gráficos), haciendo múltiples nodos en el árbol para cada nodo gráfico utilizado en múltiples caminos
• Cualquier jerarquía matemática

Las estructuras de árbol a menudo se usan para mapear las relaciones entre cosas, como:

• Componentes y subcomponentes que se pueden visualizar en un dibujo de visión explosiva
• Subroutine llamadas utilizadas para identificar qué subrutinas en un programa llaman a otras subrutinas no recursivamente
• Herencia de ADN entre especies por evolución, de código fuente por proyectos de software (por ejemplo, cronograma de distribución Linux), de diseños en diversos tipos de automóviles, etc.
• El contenido de los espacios jerárquicos

Los documentos JSON y YAML se pueden considerar como árboles, pero normalmente se representan mediante listas anidadas y diccionarios.

Terminología

Un nodo es una estructura que puede contener datos y conexiones a otros nodos, a veces llamados bordes o enlaces. Cada nodo en un árbol tiene cero o más nodos secundarios, que están debajo de él en el árbol (por convención, los árboles se dibujan con descendientes hacia abajo). Un nodo que tiene un hijo se denomina nodo padre del hijo (o superior). Todos los nodos tienen exactamente un padre, excepto el nodo raíz superior, que no tiene ninguno. Un nodo puede tener muchos nodos antepasados, como el padre del padre. Los nodos secundarios con el mismo padre son nodos hermanos. Por lo general, los hermanos tienen un orden, y el primero se dibuja convencionalmente a la izquierda. Algunas definiciones permiten que un árbol no tenga ningún nodo, en cuyo caso se llama vacío.

Un nodo interno (también conocido como nodo interno, inodo para abreviar o nodo de rama) es cualquier nodo de un árbol que tiene nodos secundarios. De manera similar, un nodo externo (también conocido como nodo externo, nodo de hoja o nodo terminal) es cualquier nodo que no tiene nodos secundarios.

La altura de un nodo es la longitud del camino descendente más largo hasta una hoja desde ese nodo. La altura de la raíz es la altura del árbol. La profundidad de un nodo es la longitud de la ruta a su raíz (es decir, su ruta raíz). Cuando se utiliza el conteo basado en cero, el nodo raíz tiene profundidad cero, los nodos hoja tienen altura cero y un árbol con un solo nodo (por lo tanto, una raíz y una hoja) tiene profundidad y altura cero. Convencionalmente, un árbol vacío (árbol sin nodos, si se permiten) tiene una altura −1.

Cada nodo no raíz puede tratarse como el nodo raíz de su propio subárbol, que incluye ese nodo y todos sus descendientes.

Otros términos usados con árboles:

Vecino

Padre o niño.

Ancestro

Un nodo alcanzable mediante procedimientos repetidos de niño a padre.

Descendiente

Un nodo alcanzable mediante procedimientos repetidos de padres a hijos. También conocido como subchild.

Grado

Para un nodo dado, su número de niños. Una hoja tiene necesariamente grado cero.

Grado de árbol

El grado de un árbol es el grado máximo de un nodo en el árbol.

Distancia

El número de bordes a lo largo del camino más corto entre dos nodos.

Nivel

El nivel de un nodo es el número de bordes a lo largo de la único camino entre él y el nodo raíz.

Esto es lo mismo que la profundidad al usar la cuenta cero.

Width

El número de nodos en un nivel.

Breadth

El número de hojas.

Forest

Un conjunto de uno o más árboles descomunales.

Árbol ordenado

Un árbol enraizado en el que se especifica un pedido para los hijos de cada vértice. El libro El arte de la programación informática utiliza el término árbol orientado.

Tamaño de un árbol

Número de nodos en el árbol.

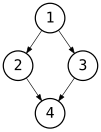
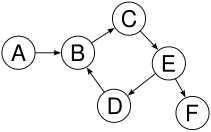
Ejemplos de árboles y no árboles

No es un árbol: two non-connected parts, A→B and C→D→E. Hay más de una raíz.

No es un árbol: ciclo no dirigido 1-2-4-3. 4 tiene más de un padre (punto de entrada).

No es un árbol: cycle B→C→E→D→B. B tiene más de un padre (punto de entrada).

No es un árbol: cycle A→A. A es la raíz, pero también tiene un padre.

Cada lista lineal es trivial un árbol

Operaciones comunes

• Enumerating all the items
• Enumerating una sección de un árbol
• Búsqueda de un artículo
• Añadiendo un nuevo elemento en una posición determinada sobre el árbol
• Eliminar un artículo
• Pruning: Eliminación de toda una sección de un árbol
• Injerto: Agregar una sección entera a un árbol
• Encontrar la raíz para cualquier nodo
• Encontrar el ancestro común más bajo de dos nodos

Métodos transversales y de búsqueda

Pasar por los elementos de un árbol, por medio de las conexiones entre padres e hijos, se llama caminar por el árbol, y la acción es un paseo por el árbol. A menudo, se puede realizar una operación cuando un puntero llega a un nodo en particular. Un recorrido en el que cada nodo principal se recorre antes que sus hijos se denomina recorrido de pre-orden; un paseo en el que se recorren los niños antes de que se atraviesen sus respectivos padres se denomina paseo post-orden; un recorrido en el que se recorre el subárbol izquierdo de un nodo, luego el nodo mismo y finalmente su subárbol derecho se denomina recorrido en orden. (Este último escenario, que hace referencia a exactamente dos subárboles, un subárbol izquierdo y un subárbol derecho, asume específicamente un árbol binario). árbol; los nodos se recorren nivel por nivel, donde primero se visita el nodo raíz, seguido de sus nodos secundarios directos y sus hermanos, seguidos de sus nodos nietos y sus hermanos, etc., hasta que se hayan recorrido todos los nodos del árbol.

Representaciones

Hay muchas maneras diferentes de representar árboles. En la memoria de trabajo, los nodos suelen ser registros asignados dinámicamente con punteros a sus hijos, sus padres o ambos, así como cualquier dato asociado. Si tiene un tamaño fijo, los nodos pueden almacenarse en una lista. Los nodos y las relaciones entre nodos pueden almacenarse en un tipo especial separado de lista de adyacencia. En las bases de datos relacionales, los nodos generalmente se representan como filas de tabla, con ID de fila indexadas que facilitan los punteros entre padres e hijos.

Los nodos también se pueden almacenar como elementos en una matriz, con relaciones entre ellos determinadas por sus posiciones en la matriz (como en un montón binario).

Un árbol binario se puede implementar como una lista de listas: la cabeza de una lista (el valor del primer término) es el hijo izquierdo (subárbol), mientras que la cola (la lista del segundo y subsiguientes términos) es el hijo derecho (subárbol). Esto se puede modificar para permitir valores también, como en las expresiones S de Lisp, donde la cabeza (valor del primer término) es el valor del nodo, la cabeza de la cola (valor del segundo término) es el hijo izquierdo y la cola de la cola (lista de términos terceros y subsiguientes) es el hijo derecho.

Los árboles ordenados se pueden codificar naturalmente mediante secuencias finitas, por ejemplo, con números naturales.

Teoría de tipos

Como tipo de datos abstracto, el tipo de árbol abstracto T con valores de algún tipo E se define utilizando el tipo de bosque abstracto F (lista de árboles), por las funciones:

valor: T → E

niños: T → F

nil: () → F

nodo: E × F → T

con los axiomas:

valor(nodo(e, f) = e

niños(node(e, f) = f

En términos de teoría de tipos, un árbol es un tipo inductivo definido por los constructores nil (bosque vacío) y nodo (árbol con nodo raíz con valor dado e hijos).

Terminología matemática

Visto como un todo, una estructura de datos de árbol es un árbol ordenado, generalmente con valores adjuntos a cada nodo. Concretamente, es (si se requiere que no esté vacío):

• Un árbol enraizado con la dirección "fuera de la raíz" (un término más estrecho es una "arborecencia"), que significa:
  • Un gráfico dirigido,
  • cuyo gráfico no dirigido subyacente es un árbol (cualquier dos vértices están conectados por exactamente un camino simple),
  • con una raíz distinguida (un vértice es designado como la raíz),
  • que determina la dirección en los bordes (flechas apuntan lejos de la raíz; dado un borde, el nodo de que el borde apunta desde se llama el padre y el nodo que el borde apunta a se llama niño), junto con:
• una orden sobre los nodos infantiles de un nodo dado, y
• un valor (de algún tipo de datos) en cada nodo.

A menudo, los árboles tienen un factor de ramificación fijo (más correctamente, acotado), sobre todo teniendo siempre dos nodos secundarios (posiblemente vacíos, por lo tanto, como máximo dos no vacíos nodos secundarios), por lo tanto, un "árbol binario".

Permitir árboles vacíos hace que algunas definiciones sean más simples y otras más complicadas: un árbol enraizado no debe estar vacío, por lo tanto, si se permiten árboles vacíos, la definición anterior se convierte en "un árbol vacío o un árbol enraizado tal que....". Por otro lado, los árboles vacíos simplifican la definición del factor de ramificación fijo: con árboles vacíos permitidos, un árbol binario es un árbol tal que cada nodo tiene exactamente dos hijos, cada uno de los cuales es un árbol (posiblemente vacío). Los conjuntos completos de operaciones en el árbol deben incluir la operación de bifurcación.