Antiprisma

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En geometría, un $n$ -gonal antiprisma< /b> o $n$ -antiprism es un poliedro compuesto por dos copias directas paralelas (no imágenes especulares) de un $n$ -lados< /span> polígono, conectado por una banda alterna de $2 n$ triángulos. Se representan mediante la notación de Conway $A n$ .

Los antiprismas son una subclase de prismatoides y son un tipo (degenerado) de poliedro chato.

Los antiprismas son similares a los prismas, excepto que las bases están torcidas entre sí y que las caras laterales (que conectan las bases) son $2 n triángulos, en lugar de n cuadriláteros.$

El poliedro dual de un antiprisma $n$ -gonal es un $n$ -trapezoedro gonal.

Historia

En la intersección de la teoría de grafos moderna y la teoría de codificación, la triangulación de un conjunto de puntos ha interesado a los matemáticos desde Isaac Newton, quien infructuosamente buscó una prueba matemática del problema del número que se besa en 1694. Se discutió la existencia de antiprismas., y su nombre fue acuñado por Johannes Kepler, aunque es posible que Arquímedes los conociera previamente, ya que cumplen las mismas condiciones en caras y vértices que los sólidos de Arquímedes. Según Ericson y Zinoviev, Harold Scott MacDonald Coxeter escribió extensamente sobre el tema y fue uno de los primeros en aplicar las matemáticas de Victor Schlegel a este campo.

El conocimiento en este campo es "bastante incompleto" y "se obtuvo bastante recientemente", es decir, en el siglo XX. Por ejemplo, a partir de 2001 se había demostrado solo para un número limitado de casos no triviales que el antiprisma $n$ -gonal es la disposición matemáticamente óptima de $2 n$ puntos en el sentido de maximizar la distancia euclidiana mínima entre dos puntos cualesquiera del conjunto: en 1943 por László Fejes Tóth para 4 y 6 puntos (antiprismas digonales y trigonales, que son sólidos platónicos); en 1951 por Kurt Schütte y Bartel Leendert van der Waerden por 8 puntos (antiprisma tetragonal, que no es un cubo).

Se ha señalado que la estructura química de los compuestos binarios pertenece a la familia de los antiprismas; especialmente los de la familia de los hidruros de boro (en 1975) y los carboranos por ser isoelectrónicos. Esta es una conclusión matemáticamente real alcanzada por los estudios de los patrones de difracción de rayos X, y se deriva del trabajo de 1971 de Kenneth Wade, la fuente nominativa de las reglas de Wade de la teoría del par de electrones del esqueleto poliédrico.

Los metales de tierras raras como los lantánidos forman compuestos antiprismáticos con algunos de los haluros o algunos de los yoduros. El estudio de la cristalografía es útil aquí. Algunos lantánidos, cuando se organizan en estructuras antiprismáticas peculiares con cloro y agua, pueden formar imanes a base de moléculas.

Antiprisma derecho

Para un antiprisma con bases regulares de n-ágonos, generalmente se considera el caso en el que estas dos copias están torcidas por un ángulo de $180 / n grados.$

El eje de un polígono regular es la línea perpendicular al plano del polígono y que se encuentra en el centro del polígono.

Para un antiprisma con bases congruentes regulares $n$ -gon, torcido por un ángulo de < span class="texhtml">180/< span class="den">n grados, se obtiene más regularidad si las bases tienen el mismo eje: son coaxiales; es decir (para bases no coplanares): si la línea que conecta los centros de las bases es perpendicular a los planos de las bases. Entonces el antiprisma se llama antiprisma recto, y sus $2 n$ caras laterales son triángulos isósceles.

Antiprisma uniforme

Un uniforme $n$ -antiprisma tiene dos $n$ -gons como caras base y $2 n$ triángulos equiláteros como caras laterales.

Los antiprismas uniformes forman una clase infinita de poliedros transitivos de vértice, al igual que los prismas uniformes. Para $n = 2$ , tenemos el tetraedro regular como un antiprisma digonal (antiprisma degenerado); para $n = 3$ , el octaedro regular como un antiprisma triangular (antiprisma no degenerado).

Familia de uniforme n- antiprismos pasados
v
t
e
Nombre del Antiprismo	Antiprismos digonal	(Trigonal) Antiprismos triangular	(Tetragonal) Antiprisma cuadrado	Antiprisma pentagonal	Antiprisma hexagonal	Antiprismos heptagonal	Antiprisma Octagonal	Antiprisma enneagonal	Antiprisma Decagonal	Antiprisma hendecagonal	Antiprisma dodecagonal	...	Apeirogonal antiprisma
Imagen de poliedro												...
Imagen de revestimiento esférico												Imagen de azulado plano
Config de Vertex.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

Diagramas de Schlegel

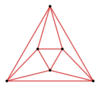A3	A4	A5	A6	A7	A8

Coordenadas cartesianas

Coordenadas cartesianas para los vértices de un $n$ -antiprisma derecho (es decir, con estilo regular $n$ -gon bases y $2 n$ caras laterales del triángulo isósceles) son:

${displaystyle left(cos {frac {kpi}{n}sin {frac {kpi}{n}},(-1)^{k}hright)}$

donde $0 \leq k \leq 2 n - 1$ ;

si el $n$ -antiprisma es uniforme (es decir, si los triángulos son equiláteros), entonces:

${displaystyle 2h^{2}=cos {fnMicroc {fnMicroc} } {n}-cos {frac {2pi} } {n}}$

Volumen y área de superficie

Sea $a$ la longitud del borde de un uniforme $n$ -antiprisma gonal; entonces el volumen es:

${displaystyle V={frac {fn} {fn} {fnfnfn} {fnfnfnfn} {fn} {fnfn}fn} {fnfn}fnfnfn}fnfnf}fnfnfnfnfnfnfnfnfnfn}fnfnfnfnfnfnfnfnfnfnfnh00fnfnfnfn}fnfnfnfnfnfnfnfnfnfnh00}fnh00}fnfn}fnfnfnfnfnfnfnfn}fnfn}fnfn}fnh00}}fnfn ################################################################################################################################################################################################################################################################ {fn} {fn} {fnK} {fn}}} {fn}} {fn}} {fn}} {fn} {fn}fn} {fn}fn} {fn} {fn}fn}fn}fnfnfnfn}fn}}}}}fn}}}}}}\\\fn}fn}\fn9fn}fn}\fnfnK\fn}fn}fn}fn}\\\\\fnK\fnK\\fn}fn}fn}\fnfn}fn}fn}fn}fn}fn}fn}\fn}fn}\fn}}\\\ }~a^{3}$

y el área de la superficie es:

${displaystyle A={frac {fn}}left {fn} {fn}fn}left(cot {fn} {fn} {fn}fn} {fn}fn}fn}fn}c}left {cot {fn}fnfnh}c}fn}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c} ¿Qué?$

Poliedros relacionados

Hay un conjunto infinito de antiprismas truncados, incluida una forma de simetría inferior del octaedro truncado (antiprisma triangular truncado). Estos se pueden alternar para crear antiprismas chatos, dos de los cuales son sólidos de Johnson, y el antiprisma triangular chato es una forma de simetría inferior del icosaedro regular.

Antiprismos
				...
s{2,4}	S{2,6}	s{2,8}	S{2,10}	s{2,2n}
Antiprismos truncados
				...
Ts{2,4}	Ts{2,6}	ts{2,8}	Ts{2,10}	Ts{2,2n}
Snub antiprismos
J₈₄	Icosahedron	J₈₅	Caras irregulares...
				...
ss{2,4}	ss{2,6}	ss{2,8}	Ss{2,10}	Ss{2,2n}

Simetría

El grupo de simetría de un $n$ -antiprisma derecho (es decir, con bases regulares y caras laterales isósceles) es $D n d = D n v$ de orden $4 n$ , excepto en los casos de:

$n = 2$ : el tetraedro regular, que tiene el grupo de simetría más grande $T d$ de orden $24 = 3\times(4\times2)$ , que tiene tres versiones de $D 2d$ como subgrupos;

$n = 3$ : el octaedro regular, que tiene el grupo de simetría más grande $O h$ de orden $48 = 4\times(4\times3)$ , que tiene cuatro versiones de $D 3d$ como subgrupos.

El grupo de simetría contiene inversión si y solo si $n$ es impar.

El grupo de rotación es $D n$ de orden $2 n$ , excepto en los casos de:

$n = 2$ : el tetraedro regular, que tiene el grupo de rotación más grande $T$ de orden $12 = 3\times(2\times2)$ , que tiene tres versiones de $D 2$ como subgrupos;

$n = 3$ : el octaedro regular, que tiene el grupo de rotación más grande $O$ de orden $24 = 4\times(2\times3)$ , que tiene cuatro versiones de $D 3$ como subgrupos.

Nota: Los $n$ -antiprismas tienen $n$ -gon y caras laterales de triángulos isósceles congruentes, por lo tanto tienen el mismo grupo de simetría (diédrica) que el uniforme $n$ -antiprisma, para $n \geq 4$ .

Estrella antiprisma

5/2-antiprism		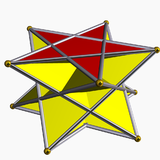	5/3-antiprism
9/2-antiprism		9/4-antiprism		9/5-antiprism

Esto muestra todos los antiprismos no estrella y estrella de hasta 15 lados, junto con los de un 29-gon.

Los antiprismas estelares uniformes se nombran por sus bases poligonales estelares, {p/q}, y existen en soluciones progradas y retrógradas (cruzadas). Las formas cruzadas tienen figuras de vértices que se intersecan y se denotan con "invertido" fracciones: p/(p – q) en lugar de p/q; ejemplo: 5/3 en lugar de 5/2.

Un antiprisma de estrella recta tiene dos caras base coaxiales regulares convexas o poligonales en estrella congruentes y 2 caras laterales de triángulos isósceles n.

Cualquier antiprisma estelar con bases regulares convexas o poligonales estelares puede convertirse en un antiprisma estelar recto (traduciendo y/o girando una de sus bases, si es necesario).

En las formas retrógradas, pero no en las formas progradas, los triángulos que unen las bases convexas o de estrella intersecan el eje de simetría rotacional. Por lo tanto:

Antiprismos de estrella retrograda con bases regulares de polígonos convexos no pueden tener todas las longitudes de borde iguales, por lo que no puede ser uniforme. "Excepción": un antiprisma estrella de retrogrado con bases triangulares equilátricas (configuración vertex: 3.3/2.3.3) puede ser uniforme; pero entonces, tiene la apariencia de un triángulo equilátero: es un poliedro estrella degenerado.

Del mismo modo, algunos antiprismos de estrellas retrogradas con bases regulares de polígono estrella no pueden tener todos los bordes iguales, por lo que no pueden ser uniformes. Ejemplo: un antiprisma estrella de retrogrado con bases estelares regulares 7/5-gon (configuración de vertex: 3.3.3.7/5) no puede ser uniforme.

Además, los compuestos antiprisma de estrella con bases regulares de estrella p/q-gon se pueden construir si p y q tienen factores comunes. Ejemplo: un antiprisma de estrella 10/4 es el compuesto de dos antiprismas de estrella 5/2.

Star p/q-antiprismos por simetría, para p ≤ 12
Grupo de Symmetry	Estrella uniforme			Estrellas derechas
D_4d [2]⁺,8] (2*4)				3.3/2.3.4
D_5h [2,5] (*225)	3.3.3.5/2			3.3/2.3.5
D_5d [2]⁺,10] (2*5)	3.3.3.5/3
D_6d [2]⁺,12] (2*6)				3.3/2.3.6
D_7h [2,7] (*227)	3.3.3.7/2	3.3.3.7/4
D_7d [2]⁺,14] (2*7)	3.3.3.7/3
D_8d [2]⁺,16] (2*8)	3.3.3.8/3	3.3.3.8/5
D_9h [2,9] (*229)	3.3.3.9/2	3.3.3.9/4
D_9d [2]⁺,18] (2*9)	3.3.3.9/5
D_10d [2]⁺,20] (2*10)	3.3.3.10/3
D_11h [2,11] (*2.11)	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
D_11d [2]⁺,22] (2*11)	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
D_12d [2]⁺,24] (2*12)	3.3.3.12/5	3.3.3.12/7
...	...

Contenido relacionado

Cinta de Moebius
Vladimir arnold
Wacław Sierpiński
Más resultados...
Te puede interesar