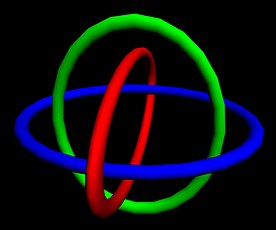
Anillos borromeos

En matemáticas, los anillos de Borromeo son tres curvas cerradas simples en el espacio tridimensional que están topológicamente unidas y no se pueden separar entre sí, pero que se descomponen en dos bucles no anudados ni unidos cuando se corta o se elimina cualquiera de las tres. Lo más común es que estos anillos se dibujen como tres círculos en el plano, siguiendo el patrón de un diagrama de Venn, cruzándose alternativamente uno sobre el otro y otro debajo en los puntos donde se cruzan. Se dice que otros triples de curvas forman los anillos de Borromeo siempre que sean topológicamente equivalentes a las curvas representadas en este dibujo.

Los anillos borromeos reciben su nombre de la casa italiana de Borromeo, que utilizó la forma circular de estos anillos como elemento de su escudo de armas, pero los diseños basados en los anillos borromeos se han utilizado en muchas culturas, incluso por los nórdicos y en Japón. Se han utilizado en el simbolismo cristiano como signo de la Trinidad y en el comercio moderno como el logotipo de la cerveza Ballantine, lo que les da el nombre alternativo de anillos Ballantine. Se han creado instancias físicas de los anillos borromeos a partir de ADN enlazado u otras moléculas, y tienen análogos en el estado de Efimov y los núcleos borromeos, los cuales tienen tres componentes unidos entre sí, aunque no hay dos de ellos unidos.

Geométricamente, los anillos borromeos pueden realizarse mediante elipses enlazadas o (utilizando los vértices de un icosaedro regular) mediante rectángulos áureos enlazados. Es imposible realizarlos utilizando círculos en el espacio tridimensional, pero se ha conjeturado que pueden realizarse mediante copias de cualquier curva simple cerrada no circular en el espacio. En la teoría de nudos, se puede demostrar que los anillos borromeos están enlazados contando sus n-coloraciones de Fox. Como enlaces, son brunnianos, alternantes, algebraicos e hiperbólicos. En topología aritmética, ciertos triples de números primos tienen propiedades de enlace análogas a los anillos borromeos.

Definición y notación

En las publicaciones matemáticas que definen los anillos de Borromeo, es común hacerlo como un diagrama de enlaces, un dibujo de curvas en el plano con cruces marcados para indicar qué curva o parte de una curva pasa por encima o por debajo en cada cruce. Tal dibujo se puede transformar en un sistema de curvas en el espacio tridimensional incrustando el plano en el espacio y deformando las curvas dibujadas en él por encima o por debajo del plano incrustado en cada cruce, como se indica en el diagrama. El diagrama comúnmente utilizado para los anillos de Borromeo consiste en tres círculos iguales centrados en los puntos de un triángulo equilátero, lo suficientemente cerca uno del otro como para que sus interiores tengan una intersección común (como en un diagrama de Venn o los tres círculos utilizados para definir el triángulo de Reuleaux). Sus cruces se alternan entre arriba y abajo cuando se consideran en orden consecutivo alrededor de cada círculo; otra forma equivalente de describir la relación de arriba-abajo entre los tres círculos es que cada círculo pasa por encima de un segundo círculo en ambos cruces, y por debajo del tercer círculo en ambos cruces. Se dice que dos enlaces son equivalentes si hay una deformación continua del espacio (una isotopía ambiental) que lleva uno al otro, y los anillos borromeos pueden referirse a cualquier enlace que sea equivalente en este sentido al diagrama estándar para este enlace.

En The Knot Atlas, los anillos borromeos se indican con el código "L6a4"; la notación significa que se trata de un enlace con seis cruces y un diagrama alterno, el cuarto de cinco enlaces alternados de 6 cruces identificados por Morwen Thistlethwaite en una lista de todos los enlaces principales con hasta 13 cruces. En las tablas de nudos y eslabones del libro de Dale Rolfsen de 1976, Knots and Links, que amplía las listas anteriores de la década de 1920 de Alexander y Briggs, los anillos borromeos recibieron la notación de Alexander-Briggs "6³
₂", lo que significa que este es el segundo de los tres eslabones de 3 componentes que se cruzan con 6 que se enumeran. La notación de Conway para los anillos borromeos, ".1", es una descripción abreviada del diagrama de enlace estándar para este enlace.

Historia y simbolismo

Valknut sobre Stora Hammars I stone

Símbolo de la Trinidad Cristiana, adaptado de un manuscrito del siglo XIII

triángulos vinculados en el Templo Marundeeswarar

El nombre de "anillos borromeos" proviene del uso de estos anillos, en forma de tres círculos enlazados, en el escudo de armas de la familia aristocrática Borromeo en el norte de Italia. El enlace en sí es mucho más antiguo y ha aparecido en forma de valknut, tres triángulos equiláteros enlazados con lados paralelos, en piedras de imágenes nórdicas que datan del siglo VII. El santuario Ōmiwa en Japón también está decorado con un motivo de los anillos borromeos, en su forma circular convencional. Un pilar de piedra en el templo Marundeeswarar del siglo VI en la India muestra tres triángulos equiláteros rotados uno respecto del otro para formar un eneagrama regular; al igual que los anillos borromeos, estos tres triángulos están enlazados y no enlazados por pares, pero este patrón cruzado describe un enlace diferente al de los anillos borromeos.

Los anillos borromeos se han utilizado en diferentes contextos para indicar la fuerza en la unidad. En particular, algunos han utilizado el diseño para simbolizar la Trinidad. Un manuscrito francés del siglo XIII que representaba los anillos borromeos etiquetados como unidad en la trinidad se perdió en un incendio en la década de 1940, pero fue reproducido en un libro de 1843 por Adolphe Napoléon Didron. Didron y otros han especulado que la descripción de la Trinidad como tres círculos iguales en el canto 33 del Paraíso de Dante se inspiró en imágenes similares, aunque Dante no detalla la disposición geométrica de estos círculos. El psicoanalista Jacques Lacan encontró inspiración en los anillos borromeos como modelo para su topología de la subjetividad humana, donde cada anillo representa un componente lacaniano fundamental de la realidad (lo "real", lo "imaginario" y lo "simbólico").

Los anillos se utilizaron como logotipo de la cerveza Ballantine y todavía se utilizan en la marca de cerveza Ballantine, que ahora distribuye el actual propietario de la marca, Pabst Brewing Company. Por este motivo, a veces se los ha llamado "anillos Ballantine".

El primer trabajo de teoría de nudos que incluyó los anillos de Borromeo fue un catálogo de nudos y enlaces compilado en 1876 por Peter Tait. En matemáticas recreativas, los anillos de Borromeo fueron popularizados por Martin Gardner, quien presentó superficies de Seifert para los anillos de Borromeo en su columna de septiembre de 1961 "Juegos matemáticos" en Scientific American. En 2006, la Unión Matemática Internacional decidió en el 25.º Congreso Internacional de Matemáticos en Madrid, España, utilizar un nuevo logotipo basado en los anillos de Borromeo.

Anillos parciales y múltiples

En la Europa medieval y renacentista, una serie de signos visuales consisten en tres elementos entrelazados de la misma manera que se muestran entrelazados los anillos borromeos (en su representación bidimensional convencional), pero con elementos individuales que no son bucles cerrados. Ejemplos de tales símbolos son los cuernos de piedra de Snoldelev y las medialunas de Diana de Poitiers.

Algunos vínculos de la teoría de nudos contienen múltiples configuraciones de anillos borromeos; un vínculo de cinco bucles de este tipo se utiliza como símbolo en el discordianismo, basándose en una representación en los Principia Discordia.

Propiedades matemáticas

Vinculación

En la teoría de nudos, los anillos borromeos son un ejemplo simple de un vínculo bruniano, un vínculo que no se puede separar, sino que se deshace en bucles separados y sin nudos tan pronto como se elimina cualquiera de sus componentes. Hay infinitos vínculos brunnianos y infinitos vínculos brunnianos de tres curvas, de los cuales los anillos borromeos son los más simples.

Hay varias maneras de ver que los anillos Borromean están vinculados. Uno es utilizar los n-colorantes Fox, los colores de los arcos de un diagrama de enlace con el modulo n enteros para que en cada cruce, los dos colores en el subcrossing tengan el mismo promedio (modulo) n) como el color del arco cruzando, y por lo que al menos dos colores se utilizan. El número de colorantes que cumplen estas condiciones es un nudo invariante, independiente del diagrama elegido para el enlace. Un enlace trivial con tres componentes tiene n3− − n{displaystyle No. colorantes, obtenidos de su diagrama estándar eligiendo un color independientemente para cada componente y descartando el n{displaystyle n} colorantes que solo usan un color. Para el diagrama estándar de los anillos Borromean, por otro lado, los mismos pares de arcos se encuentran en dos subcrossings, forzando los arcos que cruzan sobre ellos para tener el mismo color que el otro, de lo que sigue que los únicos colores que cumplen las condiciones de cruce violan la condición de utilizar más de un color. Debido a que el enlace trivial tiene muchos colores válidos y los anillos Borromean no tienen ninguno, no pueden ser equivalentes.

Los anillos borromeos son un enlace alterno, ya que su diagrama de enlace convencional tiene cruces que alternan entre pasar por encima y por debajo de cada curva, en orden a lo largo de la curva. También son un enlace algebraico, un enlace que puede descomponerse mediante esferas de Conway en 2-enredos. Son el enlace algebraico alterno más simple que no tiene un diagrama que sea al mismo tiempo alterno y algebraico. De las conjeturas de Tait se deduce que el número de cruces de los anillos borromeos (el menor número de cruces en cualquiera de sus diagramas de enlace) es 6, el número de cruces en su diagrama alterno.

Forma de anillo

Realización de anillos Borromean usando elipses

Tres rectángulos dorados ligados en un icosahedron regular

Los anillos borromeos se dibujan típicamente con sus anillos proyectados hacia círculos en el plano del dibujo, pero los anillos borromeos circulares tridimensionales son un objeto imposible: no es posible formar los anillos borromeos a partir de círculos en el espacio tridimensional. De manera más general, Michael H. Freedman y Richard Skora (1987) demostraron utilizando geometría hiperbólica de cuatro dimensiones que ningún enlace brunniano puede ser exactamente circular. Para tres anillos en su disposición borromea convencional, esto se puede ver al considerar el diagrama de enlaces. Si uno supone que dos de los círculos se tocan en sus dos puntos de cruce, entonces se encuentran en un plano o una esfera. En cualquier caso, el tercer círculo debe pasar por este plano o esfera cuatro veces, sin encontrarse en él, lo cual es imposible. Otro argumento a favor de la imposibilidad de realizaciones circulares, por Helge Tverberg, utiliza geometría inversa para transformar tres círculos cualesquiera de modo que uno de ellos se convierta en una línea, lo que hace más fácil argumentar que los otros dos círculos no se enlazan con él para formar los anillos borromeos.

Sin embargo, los anillos borromeos pueden realizarse utilizando elipses. Estas pueden considerarse de una excentricidad arbitrariamente pequeña: no importa cuán cercana a la circular sea su forma, siempre que no sean perfectamente circulares, pueden formar enlaces borromeos si se las coloca adecuadamente. Una realización de los anillos borromeos mediante tres rectángulos áureos mutuamente perpendiculares puede encontrarse dentro de un icosaedro regular conectando tres pares opuestos de sus aristas. Cada tres polígonos no anudados en el espacio euclidiano pueden combinarse, después de una transformación de escala adecuada, para formar los anillos borromeos. Si los tres polígonos son planos, entonces no es necesario escalar. En particular, debido a que los anillos borromeos pueden realizarse mediante tres triángulos, el número mínimo de lados posible para cada uno de sus bucles, el número de varillas de los anillos borromeos es nueve.

En términos más generales, Matthew Cook ha conjeturado que tres curvas simples cerradas y sin anudar en el espacio, no todas círculos, pueden combinarse sin escalar para formar los anillos borromeos. Después de que Jason Cantarella sugiriera un posible contraejemplo, Hugh Nelson Howards debilitó la conjetura para aplicarla a tres curvas planas cualesquiera que no sean todas círculos. Por otro lado, aunque hay infinitos enlaces brunnianos con tres enlaces, los anillos borromeos son los únicos que pueden formarse a partir de tres curvas convexas.

Longitud de la cuerda

En la teoría del nudo, la longitud de la cuerda de un nudo o un enlace es la longitud más corta de la cuerda flexible (del radio uno) que puede darse cuenta. Matemáticamente, tal realización puede ser descrita por una curva suave cuyo vecindario radius-one tubular evita las intersecciones propias. La longitud mínima de la cuerda de los anillos Borromean no ha sido probada, pero el valor más pequeño que se ha alcanzado se realiza por tres copias de una curva plana de 2 lóbulos. Aunque se asemeja a un candidato anterior para la longitud mínima de la cuerda, construido a partir de cuatro arcos circulares del radio dos, se modifica ligeramente de esa forma, y se compone de 42 piezas lisas definidas por integrales elípticos, lo que lo hace más corto por una fracción de un porcentaje que la realización circular de la pieza. Es esta realización, conjeturada para minimizar la longitud de la cuerda, que se utilizó para el logotipo de la Unión Matemática Internacional. Su longitud es . . 58.006{displaystyle approx 58.006}, mientras que el límite inferior mejor probado en la longitud es 12π π . . 37,699{displaystyle 12pi approx 37.699}.

Para un análogo discreto de longitud de la cuerda, la representación más corta usando sólo los bordes de la rejilla del entero, la longitud mínima para los anillos Borromean es exactamente 36{displaystyle 36}. Esta es la longitud de una representación usando tres 2× × 4{displaystyle 2times 4} rectángulos enteros, inscritos en el icosahedro de Jessen de la misma manera que la representación por rectángulos dorados se inscribe en el icosahedro regular.

Geometría hiperbólica

Los anillos Borromean son un enlace hiperbólico: el espacio que rodea los anillos Borromean (su complemento de enlace) admite una métrica hiperbólica completa de volumen finito. Aunque los enlaces hiperbólicos se consideran ahora abundantes, los anillos Borromean fueron uno de los primeros ejemplos que se probaron hiperbólicos, en la década de 1970, y este complemento de enlace fue un ejemplo central en el vídeo No., producido en 1991 por el Centro de Geometría.

Los manifolds hiperbólicos se pueden descomponer de forma canónica en los encolamientos de poliedros hiperbólicos (la descomposición Epstein-Penner) y para el complemento Borromeano esta descomposición consiste en dos octahedra regular ideal. El volumen del complemento Borromeano es 16▪ ▪ ()π π /4)=8G. . 7.32772... ... {displaystyle 16Lambda (pi /4)=8Gapprox 7.32772dots } Donde ▪ ▪ {displaystyle Lambda } es la función Lobachevsky y G{displaystyle G. es la constante de catalán. El complemento de los anillos Borromean es universal, en el sentido de que cada doble cerrado es una cubierta ramificada sobre este espacio.

Teoría de números

En topología aritmética, existe una analogía entre los nudos y los números primos en la que se consideran los vínculos entre primos. El triple de primos (13, 61, 937) están vinculados módulo 2 (el símbolo de Rédei es −1) pero no están vinculados módulo 2 por pares (los símbolos de Legendre son todos 1). Por lo tanto, estos primos se han denominado "triple borromeana propia módulo 2" o "primos borromeos mod 2".

Realizaciones físicas

El nudo del puño de un mono es esencialmente una representación tridimensional de los anillos borromeos, aunque con tres capas, en la mayoría de los casos. El escultor John Robinson ha realizado obras de arte con tres triángulos equiláteros hechos de chapa metálica, unidos para formar anillos borromeos y que se asemejan a una versión tridimensional del valknut. Un diseño común para un trípode de madera plegable consiste en tres piezas talladas a partir de una sola pieza de madera, y cada pieza consta de dos trozos de madera, las patas y los lados superiores del trípode, conectados por dos segmentos de madera que rodean un orificio central alargado en la pieza. Otra de las tres piezas pasa a través de cada uno de estos orificios, uniendo las tres piezas en el patrón de anillos borromeos. Los trípodes de esta forma se han descrito como provenientes de artesanías indias o africanas.

En química, los anillos de Borromeo moleculares son las contrapartes moleculares de los anillos de Borromeo, que son arquitecturas moleculares entrelazadas mecánicamente. En 1997, el biólogo Chengde Mao y sus colaboradores de la Universidad de Nueva York lograron construir un conjunto de anillos a partir del ADN. En 2003, el químico Fraser Stoddart y sus colaboradores de la UCLA utilizaron la química de coordinación para construir un conjunto de anillos en un solo paso a partir de 18 componentes. Las estructuras de anillos de Borromeo se han utilizado para describir cúmulos de metales nobles protegidos por una capa superficial de ligandos de tiolato. Giuseppe Resnati y sus colaboradores han sintetizado una biblioteca de redes de Borromeo diseñadas por autoensamblaje impulsado por enlaces halógenos. Para acceder al anillo de Borromeo molecular que consta de tres ciclos desiguales, Jay S. Siegel y sus colaboradores propusieron una síntesis paso a paso.

En física, un análogo mecánico cuántico de los anillos de Borromeo se denomina estado de halo o estado de Efimov, y consiste en tres partículas ligadas que no están ligadas por pares. La existencia de tales estados fue predicha por el físico Vitaly Efimov en 1970 y confirmada por múltiples experimentos a partir de 2006. Este fenómeno está estrechamente relacionado con un núcleo de Borromeo, un núcleo atómico estable que consiste en tres grupos de partículas que serían inestables en pares. Otro análogo de los anillos de Borromeo en la teoría de la información cuántica implica el entrelazamiento de tres cúbits en el estado de Greenberger-Horne-Zeilinger.

• 
  Un nudo de puño de mono
• 
  Borromean anillo de punto proyecto por el teórico de nudos Laura Taalman
• 
  Anillos moleculares de Borromean