Ángulo recto
En geometría y trigonometría, a ángulo recto es un ángulo de exactamente 90 grados o /2 radios correspondientes a un giro trimestral. Si se coloca un rayo para que su punto final esté en línea y los ángulos adyacentes sean iguales, entonces son ángulos rectos. El término es un calque de latín angulus rectus; aquí recto significa "derecha", refiriéndose al perpendicular vertical a una línea de base horizontal.
Los conceptos geométricos importantes y estrechamente relacionados son las líneas perpendiculares, es decir, las líneas que forman ángulos rectos en su punto de intersección, y la ortogonalidad, que es la propiedad de formar ángulos rectos, generalmente aplicada a los vectores. La presencia de un ángulo recto en un triángulo es el factor definitorio de los triángulos rectángulos, lo que hace que el ángulo recto sea básico para la trigonometría.
Etimología
El significado de recto en ángulo recto posiblemente se refiera al adjetivo latino rectus 'erecto, recto, erguido, perpendicular&# 39;. Un equivalente griego es orthos 'recto; perpendicular' (ver ortogonalidad).
En geometría elemental
Un rectángulo es un cuadrilátero con cuatro ángulos rectos. Un cuadrado tiene cuatro ángulos rectos, además de los lados de igual longitud.
El teorema de Pitágoras establece cómo determinar cuándo un triángulo es un triángulo rectángulo.
Símbolos
En Unicode, el símbolo de un ángulo recto es U+221F ∟ ÁNGULO RECTO (∟). No debe confundirse con el símbolo de forma similar U+231E ⌞ ESQUINA INFERIOR IZQUIERDA (⌞, ⌞ ). Los símbolos relacionados son U+22BE ⊾ ÁNGULO RECTO CON ARCO (⊾), U+299C ⦜ VARIANTE DE ÁNGULO RECTO CON CUADRADO (⦜) y U+299D ⦝ ÁNGULO RECTO MEDIDO CON PUNTO (⦝).
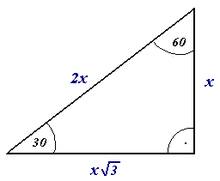
En los diagramas, el hecho de que un ángulo sea un ángulo recto generalmente se expresa agregando un pequeño ángulo recto que forma un cuadrado con el ángulo en el diagrama, como se ve en el diagrama de un triángulo rectángulo (en inglés británico, a triángulo rectángulo) a la derecha. El símbolo de un ángulo medido, un arco, con un punto, se usa en algunos países europeos, incluidos los países de habla alemana y Polonia, como símbolo alternativo para un ángulo recto.
Euclides
Los ángulos rectos son fundamentales en los Elementos de Euclides. Se definen en el Libro 1, definición 10, que también define líneas perpendiculares. La definición 10 no utiliza medidas numéricas en grados, sino que toca el corazón mismo de lo que es un ángulo recto, es decir, dos líneas rectas que se cruzan para formar dos ángulos iguales y adyacentes. Las rectas que forman ángulos rectos se llaman perpendiculares. Euclides usa ángulos rectos en las definiciones 11 y 12 para definir ángulos agudos (aquellos menores que un ángulo recto) y ángulos obtusos (aquellos mayores que un ángulo recto). Dos ángulos se llaman complementarios si su suma es un ángulo recto.
El Postulado 4 del Libro 1 establece que todos los ángulos rectos son iguales, lo que le permite a Euclides usar un ángulo recto como unidad para medir otros ángulos. El comentarista de Euclides, Proclo, dio una prueba de este postulado usando los postulados anteriores, pero se puede argumentar que esta prueba hace uso de algunas suposiciones ocultas. Saccheri también dio una prueba pero usando una suposición más explícita. En la axiomatización de la geometría de Hilbert, esta declaración se da como un teorema, pero solo después de mucho trabajo preliminar. Se puede argumentar que, incluso si el postulado 4 puede probarse a partir de los anteriores, en el orden en que Euclides presenta su material es necesario incluirlo ya que sin él el postulado 5, que usa el ángulo recto como unidad de medida, no hace nada. sentido.
Conversión a otras unidades
Un ángulo recto se puede expresar en diferentes unidades:
- 1/4 turno
- 90° (de acuerdo)
- π/2 radiantes
- 100 grad (también llamado grado, gradian, o Gon)
- 8 puntos (de una brújula de 32 puntos)
- 6 horas (ángulo de hora astronómica)
Regla de 3-4-5
A lo largo de la historia, los carpinteros y albañiles han conocido una forma rápida de confirmar si un ángulo es un verdadero "ángulo recto". Se basa en la terna pitagórica más conocida (3, 4, 5) y llamada la "regla de 3-4-5". Desde el ángulo en cuestión, trazar una línea recta a lo largo de un lado exactamente de 3 unidades de longitud, y a lo largo del segundo lado de exactamente 4 unidades de longitud, creará una hipotenusa (la línea más larga opuesta al ángulo recto que conecta los dos extremos medidos) de exactamente 5 unidades de longitud. Esta medición se puede realizar rápidamente y sin instrumentos técnicos. La ley geométrica detrás de la medida es el teorema de Pitágoras ("El cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de los dos lados adyacentes").
Tales' teorema
animación al final con pausa 10 s
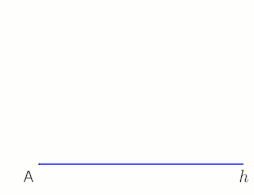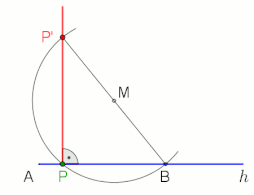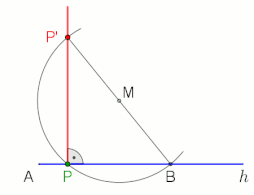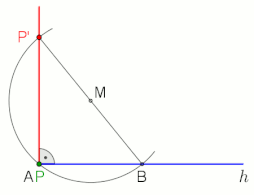
Thales' El teorema establece que un ángulo inscrito en un semicírculo (con un vértice en el semicírculo y sus rayos definidores que pasan por los extremos del semicírculo) es un ángulo recto.
Dos ejemplos de aplicación en los que el ángulo recto y el Thales' teorema están incluidos (ver animaciones).