Análisis nodal

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Método en el análisis de circuitos eléctricos

La ley actual de Kirchhoff es la base del análisis nodal.

En el análisis de circuitos eléctricos, el análisis nodal, el análisis de voltaje de nodo o el método de corriente de rama es un método para determinar el voltaje ( diferencia de potencial) entre "nodos" (puntos donde se conectan elementos o ramas) en un circuito eléctrico en términos de las corrientes de rama.

El análisis nodal es esencialmente una aplicación sistemática de la ley de corrientes de Kirchhoff (KCL) para el análisis de circuitos. De manera similar, el análisis de malla es una aplicación sistemática de la ley de voltaje de Kirchhoff (KVL). El análisis nodal escribe una ecuación en cada nodo eléctrico que especifica que las corrientes derivadas que inciden en un nodo deben sumar cero (esto es solo KCL). Las corrientes de rama se escriben en términos de los voltajes de los nodos del circuito. Como consecuencia, cada relación constitutiva de rama debe dar corriente en función del voltaje; una representación de admisión. Por ejemplo, para una resistencia, I_rama = V_rama * G, donde G (=1/R) es la admitancia (conductancia) de la resistencia.

El análisis nodal es posible cuando todos los elementos del circuito' Las relaciones constitutivas de rama tienen una representación de admisión. El análisis nodal produce un conjunto compacto de ecuaciones para la red, que se puede resolver a mano si es pequeña, o se puede resolver rápidamente usando álgebra lineal por computadora. Debido al sistema compacto de ecuaciones, muchos programas de simulación de circuitos (por ejemplo, SPICE) utilizan el análisis nodal como base. Cuando los elementos no tienen representaciones de admitancia, se puede utilizar una extensión más general del análisis nodal, el análisis nodal modificado.

Procedimiento

Nota todos los segmentos de alambre conectados en el circuito. Estos son los nodos de análisis nodal.
Seleccione un nodo como referencia de tierra. La elección no afecta los voltajes de elementos (pero afecta los voltajes nodal) y es sólo una cuestión de convención. Elegir el nodo con la mayoría de las conexiones puede simplificar el análisis. Para un circuito de N nodos el número de ecuaciones nodal es N−1.
Asignar una variable para cada nodo cuyo voltaje es desconocido. Si el voltaje ya es conocido, no es necesario asignar una variable.
Para cada voltaje desconocido, forma una ecuación basada en la Ley actual de Kirchhoff (es decir, agrega todas las corrientes que salen del nodo y marca la suma igual a cero). La corriente entre dos nodos es igual al voltaje del nodo donde las salidas actuales menos el voltaje del nodo donde la corriente entra en el nodo, ambos divididos por la resistencia entre los dos nodos.
Si hay fuentes de tensión entre dos voltajes desconocidos, únete a los dos nodos como supernodo. Las corrientes de los dos nodos se combinan en una sola ecuación, y se forma una nueva ecuación para los voltajes.
Resolver el sistema de ecuaciones simultáneas para cada voltaje desconocido.

Ejemplos

Caso básico

El único voltaje desconocido en este circuito es ${displaystyle V_{1}}$ . Hay tres conexiones con este nodo y, en consecuencia, tres corrientes a considerar. La dirección de las corrientes en cálculos es elegida para estar lejos del nodo.

Corriente a través de resistor ${displaystyle R_{1}}$ : ${displaystyle (V_{1}-V_{S})/R_{1}}$
Corriente a través de resistor ${displaystyle R_{2}}$ : ${displaystyle V_{1}/R_{2}}$
Corriente por fuente actual ${displaystyle I_{S}}$ : ${displaystyle -I_{S}}$

Con la ley actual de Kirchhoff, obtenemos:

{displaystyle {frac {V_{1}-V_{S}}{R_{1}}}+{frac {V_{1}}{R_{2}}}-I_{S}=0}

Esta ecuación se puede resolver con respecto a V₁:

{displaystyle V_{1}={frac {left({frac {V_{S}}{R_{1}}}+I_{S}right)}{left({frac {1}{R_{1}}}+{frac {1}{R_{2}}}right)}}}

Finalmente, el voltaje desconocido se puede resolver sustituyendo los símbolos por valores numéricos. Cualquier corriente desconocida es fácil de calcular una vez que se conocen todos los voltajes del circuito.

{displaystyle V_{1}={frac {left({frac {5{text{ V}}}{100,Omega }}+20{text{ mA}}right)}{left({frac {1}{100,Omega }}+{frac {1}{200,Omega }}right)}}={frac {14}{3}}{text{ V}}}

Supernodos

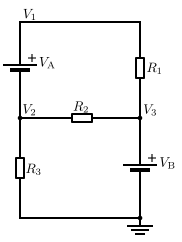
En este circuito, inicialmente tenemos dos voltajes desconocidos, V₁ y V₂. Ya se sabe que el voltaje en V₃ es V_B porque el otro terminal de la fuente de voltaje está en potencial de tierra.

La corriente que pasa por la fuente de voltaje V_A no se puede calcular directamente. Por lo tanto, no podemos escribir las ecuaciones actuales ni para V₁ ni para V₂. Sin embargo, sabemos que el mismo nodo saliente actual V₂ debe ingresar al nodo V₁. Aunque los nodos no se pueden resolver individualmente, sabemos que la corriente combinada de estos dos nodos es cero. Esta combinación de los dos nodos se llama técnica del supernodo y requiere una ecuación adicional: V₁ = V₂ + V_A.

El conjunto completo de ecuaciones para este circuito es:

{displaystyle {begin{cases}{frac {V_{1}-V_{text{B}}}{R_{1}}}+{frac {V_{2}-V_{text{B}}}{R_{2}}}+{frac {V_{2}}{R_{3}}}=0\V_{1}=V_{2}+V_{text{A}}\end{cases}}}

Al sustituir

{displaystyle V_{2}={frac {(R_{1}+R_{2})R_{3}V_{text{B}}-R_{2}R_{3}V_{text{A}}}{(R_{1}+R_{2})R_{3}+R_{1}R_{2}}}}

Forma matricial para la ecuación de tensión de nodo

En general, para un circuito con ${displaystyle N}$ nodos, las ecuaciones de node-voltaje obtenidas por análisis nodal pueden ser escritas en una forma de matriz como derivada en lo siguiente. Para cualquier nodo ${displaystyle k}$ , estados KCL ${textstyle sum _{jneq k}G_{jk}(v_{k}-v_{j})=0}$ Donde ${displaystyle G_{kj}=G_{jk}}$ es el negativo de la suma de las conductas entre los nodos ${displaystyle k}$ y ${displaystyle j}$ , y ${displaystyle v_{k}}$ es el voltaje del nodo ${displaystyle k}$ . Esto implica ${textstyle 0=sum _{jneq k}G_{jk}(v_{k}-v_{j})=sum _{jneq k}G_{jk}v_{k}-sum _{jneq k}G_{jk}v_{j}=G_{kk}v_{k}-sum _{jneq k}G_{jk}v_{j}}$ Donde ${displaystyle G_{kk}}$ es la suma de las conductas relacionadas con el nodo ${displaystyle k}$ . Observamos que el primer término contribuye linealmente al nodo ${displaystyle k}$ via ${displaystyle G_{kk}}$ , mientras que el segundo término contribuye linealmente a cada nodo ${displaystyle j}$ conectado al nodo ${displaystyle k}$ via ${displaystyle G_{jk}}$ con menos señal. If an independent current source/input ${displaystyle i_{k}}$ se adjunta también al nodo ${displaystyle k}$ , la expresión anterior se generaliza ${textstyle i_{k}=G_{kk}v_{k}-sum _{jneq k}G_{jk}v_{j}}$ . Se muestra fácilmente que uno puede combinar las ecuaciones de nodo-voltaje anteriores para todos ${displaystyle N}$ nodos, y escribirlos en la siguiente forma de matriz

{displaystyle {begin{pmatrix}G_{11}&G_{12}&cdots &G_{1N}\G_{21}&G_{22}&cdots &G_{2N}\vdots &vdots &ddots &vdots \G_{N1}&G_{N2}&cdots &G_{NN}end{pmatrix}}{begin{pmatrix}v_{1}\v_{2}\vdots \v_{N}end{pmatrix}}={begin{pmatrix}i_{1}\i_{2}\vdots \i_{N}end{pmatrix}}}

{textstyle mathbf {Gv} =mathbf {i}.}

La matriz ${displaystyle mathbf {G} }$ en el lado izquierdo de la ecuación es singular ya que satisface ${displaystyle mathbf {G1} =0}$ Donde ${displaystyle mathbf {1} }$ es un ${displaystyle Ntimes 1}$ matriz de columna que contiene sólo 1s. Esto corresponde al hecho de la conservación actual, a saber, ${textstyle sum _{k}i_{k}=0}$ , y la libertad de elegir un nodo de referencia (tierra). En la práctica, el voltaje en el nodo de referencia se toma a 0. Considera que es el último nodo, ${displaystyle v_{N}=0}$ . En este caso, es sencillo verificar que las ecuaciones resultantes para el otro ${displaystyle N-1}$ los nodos siguen siendo los mismos, y por lo tanto uno simplemente puede descartar la última columna así como la última línea de la ecuación matriz. Este procedimiento resulta en un ${displaystyle (N-1)times (N-1)}$ Ecuación de matriz dimensional no singular con las definiciones de todos los elementos permanecen inalterados.

Contenido relacionado

Más resultados...