Análisis de malla

Análisis de malla (o el método de corriente de malla ) es un método de análisis de circuitos para circuitos planos. Los circuitos planos son circuitos que se pueden dibujar en una superficie plana sin cables que se cruzan entre sí. Una técnica más general, llamada análisis de bucle (con las variables de red correspondientes llamadas corrientes de bucle ) se puede aplicar a cualquier circuito, plano o no. El análisis de malla y el análisis de bucle hacen el uso sistemático de la ley de voltaje de Kirchhoff para llegar a un conjunto de ecuaciones garantizadas para ser solucionables si el circuito tiene una solución. El análisis de malla suele ser más fácil de usar cuando el circuito es plano, en comparación con el análisis de bucle.

corrientes de malla y mallas esenciales

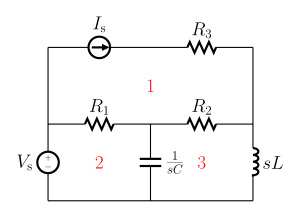
El análisis de malla funciona asignando arbitrariamente corrientes de malla en las mallas esenciales (también denominadas mallas independientes). Una malla esencial es un bucle en el circuito que no contiene ningún otro bucle. La Figura 1 etiqueta las mallas esenciales con uno, dos y tres.

Una corriente de malla es una corriente que circula alrededor de la malla esencial y las ecuaciones se resuelven en términos de ellas. Es posible que una corriente de malla no corresponda a ninguna corriente que fluya físicamente, pero las corrientes físicas se encuentran fácilmente en ellas. Es una práctica habitual que todas las corrientes de malla circulen en la misma dirección. Esto ayuda a evitar errores al escribir las ecuaciones. La convención es que todas las corrientes de malla formen un bucle en el sentido de las agujas del reloj. La Figura 2 muestra el mismo circuito de la Figura 1 con las corrientes de malla etiquetadas.

Resolver las corrientes de malla en lugar de aplicar directamente la ley de corrientes de Kirchhoff y la ley de voltaje de Kirchhoff puede reducir en gran medida la cantidad de cálculo requerido. Esto se debe a que hay menos corrientes de malla que corrientes de rama físicas. En la figura 2, por ejemplo, hay seis corrientes derivadas pero sólo tres corrientes de malla.

Configurar las ecuaciones

Cada malla produce una ecuación. Estas ecuaciones son la suma de las caídas de voltaje en un bucle completo de la corriente de malla. Para problemas más generales que aquellos que incluyen fuentes de corriente y voltaje, las caídas de voltaje serán la impedancia del componente electrónico multiplicada por la corriente de malla en ese bucle.

Si hay una fuente de voltaje presente dentro del bucle de malla, el voltaje en la fuente se suma o se resta dependiendo de si se trata de una caída de voltaje o un aumento de voltaje en la dirección de la corriente de malla. Para una fuente de corriente que no está contenida entre dos mallas (por ejemplo, la fuente de corriente en la malla esencial 1 en el circuito anterior), la corriente de malla tomará el valor positivo o negativo de la fuente de corriente dependiendo de si la corriente de malla está en dirección igual o opuesta a la de la fuente de corriente. El siguiente es el mismo circuito anterior con las ecuaciones necesarias para resolver todas las corrientes en el circuito.

{}Mesh 1: I1=IsMesh 2: − − Vs+R1()I2− − I1)+1sC()I2− − I3)=0Mesh 3: 1sC()I3− − I2)+R2()I3− − I1)+sLI3=0{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}

Una vez que se encuentran las ecuaciones, el sistema de ecuaciones lineales se puede resolver utilizando cualquier técnica para resolver ecuaciones lineales.

Casos especiales

Hay dos casos especiales en la corriente de malla: corrientes que contienen una supermesh y corrientes que contienen fuentes dependientes.

Supermesh

Una supermesh ocurre cuando una fuente de corriente está contenida entre dos mallas esenciales. El circuito se trata primero como si la fuente de corriente no estuviera allí. Esto lleva a una ecuación que incorpora dos corrientes de malla. Una vez que se forma esta ecuación, se necesita una ecuación que relacione las dos corrientes de malla con la fuente actual. Esta será una ecuación en la que la fuente actual es igual a una de las corrientes de malla menos la otra. El siguiente es un ejemplo simple de lidiar con una supermesh.

{}Mesh 1, 2: − − Vs+R1I1+R2I2=0Fuente actual: Is=I2− − I1{displaystyle {begin{cases}{text{Mesh 1, 2: }-V_{s}+R_{1}I_{1}+R_{2}I_{2}=0{text{Current fuente: }I_{s}=I_{2}-I_{1}end{cases},}

Fuentes dependientes

Una fuente dependiente es una fuente de corriente o fuente de voltaje que depende del voltaje o corriente de otro elemento en el circuito. Cuando una fuente dependiente está contenida dentro de una malla esencial, la fuente dependiente debe tratarse como una fuente independiente. Una vez formada la ecuación de malla, se necesita una ecuación fuente dependiente. Esta ecuación generalmente se denomina ecuación de restricción. Esta es una ecuación que relaciona la variable de la fuente dependiente con el voltaje o la corriente de la que depende la fuente en el circuito. El siguiente es un ejemplo sencillo de una fuente dependiente.

{}Mesh 1: − − Vs+R1I1+R3()I1− − I2)=0Mesh 2: R2I2+3Ix+R3()I2− − I1)=0Variable dependiente: Ix=I1− − I2{displaystyle {begin{cases}{text{Mesh 1: }-V_{s}+R_{1}I_{1}+R_{3}(I_{1}-I_{2})=0{text{Mesh} 2: }R_{2}I_{2}+3I_{x}+R_{3}(I_{2}-I_{1})=0\{text{Dependent variable: }I_{x}=I_{1}-I_{2}end{cases},}