Algoritmo euclidiano

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Algoritmo para computar los divisores más comunes

El método de Euclid para encontrar el mayor divisor común (GCD) de dos longitudes iniciales BA y DC, ambos definidos como múltiples de una "unidad" común longitud. La longitud DC es más corta, se utiliza para "medir" BA, pero sólo una vez porque el resto EA es menos que DC. EA ahora mide (dos veces) la longitud más corta DC, con el FC restante más corto que EA. Luego el FC mide (tres veces) longitud EA. Debido a que no hay restos, el proceso termina siendo el GCD. En el ejemplo correcto de Nicomachus con los números 49 y 21 resultando en su GCD de 7 (de Heath 1908:300).

En matemáticas, el algoritmo de Euclides, o algoritmo de Euclides, es un método eficaz para calcular el máximo común divisor (MCD) de dos enteros (números), el mayor número que los divide a ambos sin resto. Lleva el nombre del antiguo matemático griego Euclides, quien lo describió por primera vez en sus Elementos (c. 300 a. C.). Es un ejemplo de un algoritmo, un procedimiento paso a paso para realizar un cálculo de acuerdo con reglas bien definidas, y es uno de los algoritmos más antiguos de uso común. Se puede utilizar para reducir fracciones a su forma más simple y forma parte de muchos otros cálculos criptográficos y teóricos de números.

El algoritmo euclidiano se basa en el principio de que el máximo común divisor de dos números no cambia si el número mayor se reemplaza por su diferencia con el número menor. Por ejemplo, 21 es el MCD de 252 y 105 (como 252 = 21 × 12 y 105 = 21 × 5), y el mismo número 21 es también el MCD de 105 y 252 − 105 = 147. Dado que este reemplazo reduce el mayor de los dos números, la repetición de este proceso da pares de números sucesivamente más pequeños hasta que los dos números se vuelven iguales. Cuando eso ocurre, son el MCD de los dos números originales. Al invertir los pasos o usar el algoritmo euclidiano extendido, el MCD se puede expresar como una combinación lineal de los dos números originales, es decir, la suma de los dos números, cada uno multiplicado por un número entero (por ejemplo, 21 = 5 × 105 + (−2) × 252). El hecho de que el GCD siempre se pueda expresar de esta manera se conoce como identidad de Bézout.

La versión del algoritmo euclidiano descrito anteriormente (y por Euclides) puede tomar muchos pasos de resta para encontrar el GCD cuando uno de los números dados es mucho más grande que el otro. Una versión más eficiente del algoritmo abrevia estos pasos, en lugar de reemplazar el mayor de los dos números por su resto cuando se divide por el menor de los dos (con esta versión, el algoritmo se detiene cuando llega a un resto cero). Con esta mejora, el algoritmo nunca requiere más pasos que cinco veces el número de dígitos (base 10) del entero más pequeño. Esto fue probado por Gabriel Lamé en 1844 y marca el comienzo de la teoría de la complejidad computacional. En el siglo XX se desarrollaron métodos adicionales para mejorar la eficiencia del algoritmo.

El algoritmo de Euclides tiene muchas aplicaciones teóricas y prácticas. Se utiliza para reducir fracciones a su forma más simple y para realizar divisiones en aritmética modular. Los cálculos que utilizan este algoritmo forman parte de los protocolos criptográficos que se utilizan para proteger las comunicaciones de Internet y en los métodos para romper estos criptosistemas mediante la factorización de grandes números compuestos. El algoritmo euclidiano se puede usar para resolver ecuaciones diofánticas, como encontrar números que satisfagan múltiples congruencias de acuerdo con el teorema del resto chino, construir fracciones continuas y encontrar aproximaciones racionales precisas a números reales. Finalmente, se puede utilizar como una herramienta básica para probar teoremas en la teoría de números, como el teorema de los cuatro cuadrados de Lagrange y la unicidad de las factorizaciones primas.

El algoritmo original se describió solo para números naturales y longitudes geométricas (números reales), pero el algoritmo se generalizó en el siglo XIX a otros tipos de números, como enteros gaussianos y polinomios de una variable. Esto condujo a nociones algebraicas abstractas modernas como los dominios euclidianos.

Antecedentes: máximo común divisor

El algoritmo euclidiano calcula el máximo común divisor (MCD) de dos números naturales a y b. El máximo común divisor g es el mayor número natural que divide a a y b sin dejar resto. Los sinónimos de GCD incluyen máximo común divisor (MCD), máximo común divisor (HCF), máximo común divisor (HCD) y máxima medida común (MCG). El máximo común divisor a menudo se escribe como mcd(a, b) o, más simplemente, como (a, b), aunque esta última notación es ambigua, también se utiliza para conceptos como un ideal en el anillo de los números enteros, que está estrechamente relacionado con GCD.

Si mcd(a, b) = 1, entonces se dice que a y b son coprimos (o relativamente primo). Esta propiedad no implica que a o b sean en sí mismos números primos. Por ejemplo, 6 y 35 se factorizan como 6 = 2 × 3 y 35 = 5 × 7, por lo que no son primos, pero sus factores primos son diferentes, por lo que 6 y 35 son coprimos, sin factores comunes distintos de 1.

"Tall, slender rectangle divided into a grid of squares. The rectangle is two squares wide and five squares tall."

Un rectángulo de 24 por 60 está cubierto con diez azulejos cuadrados de 12 por 12, donde 12 es el GCD de 24 y 60. Más generalmente, un a-por-b rectángulo se puede cubrir con azulejos cuadrados de longitud lateral c sólo si c es un divisor común a y b.

Sea g = mcd(a, b). Como a y b son múltiplos de g, se pueden escribir a = mg y b = ng, y no hay un número mayor G > g para los cuales esto es cierto. Los números naturales m y n deben ser coprimos, ya que cualquier factor común podría factorizarse a partir de m y n para hacer g mayor. Por lo tanto, cualquier otro número c que divide tanto a a como a b también debe dividir a g. El máximo común divisor g de a y b es el único divisor común (positivo) de a y b que es divisible por cualquier otro divisor común c.

El máximo común divisor se puede visualizar de la siguiente manera. Considere un área rectangular a por b, y cualquier divisor común c que divide tanto a como b exactamente. Los lados del rectángulo se pueden dividir en segmentos de longitud c, lo que divide el rectángulo en una cuadrícula de cuadrados de longitud lateral c. El GCD g es el mayor valor de c para el que esto es posible. Por ejemplo, un área rectangular de 24 por 60 se puede dividir en una cuadrícula de: cuadrados de 1 por 1, cuadrados de 2 por 2, cuadrados de 3 por 3, cuadrados de 4 por 4, cuadrados de 6 por -6 cuadrados o cuadrados de 12 por 12. Por lo tanto, 12 es el MCD de 24 y 60. Un área rectangular de 24 por 60 se puede dividir en una cuadrícula de 12 por 12 cuadrados, con dos cuadrados a lo largo de un borde (24/12 = 2) y cinco cuadrados a lo largo el otro (60/12 = 5).

El máximo común divisor de dos números a y b es el producto de los factores primos compartidos por los dos números, donde cada factor primo se puede repetir tantas veces as divide tanto a como b. Por ejemplo, dado que 1386 se puede factorizar en 2 × 3 × 3 × 7 × 11, y 3213 se puede factorizar en 3 × 3 × 3 × 7 × 17, el MCD de 1386 y 3213 es igual a 63 = 3 × 3 × 7, el producto de sus factores primos compartidos (con 3 repetidos ya que 3 × 3 divide a ambos). Si dos números no tienen factores primos comunes, su MCD es 1 (obtenido aquí como una instancia del producto vacío), en otras palabras, son coprimos. Una ventaja clave del algoritmo euclidiano es que puede encontrar el GCD de manera eficiente sin tener que calcular los factores primos. Se cree que la factorización de números enteros grandes es un problema computacionalmente muy difícil, y la seguridad de muchos protocolos criptográficos ampliamente utilizados se basa en su inviabilidad.

Otra definición de GCD es útil en matemáticas avanzadas, particularmente en la teoría de anillos. El máximo común divisor g de dos números distintos de cero a y b es también su combinación lineal integral positiva más pequeña, es decir, el número positivo más pequeño de la forma ua + vb donde u y v son números enteros. El conjunto de todas las combinaciones lineales integrales de a y b es en realidad el mismo que el conjunto de todos los múltiplos de g (mg, donde m es un número entero). En el lenguaje matemático moderno, el ideal generado por a y b es el ideal generado por g solo (un ideal generado por un solo elemento se llama un ideal principal, y todos los ideales de los números enteros son ideales principales). Algunas propiedades del MCD son, de hecho, más fáciles de ver con esta descripción, por ejemplo, el hecho de que cualquier divisor común de a y b también divide el MCD (divide ambos términos de ua + vb). La equivalencia de esta definición de GCD con las otras definiciones se describe a continuación.

El MCD de tres o más números es igual al producto de los factores primos comunes a todos los números, pero también se puede calcular tomando repetidamente los MCD de pares de números. Por ejemplo,

gcd(a, b, c . a, gcd(b, c) = gcd(gcd(a, b), c) = gcd(gcd(a, c), b).

Por lo tanto, el algoritmo de Euclides, que calcula el MCD de dos enteros, es suficiente para calcular el MCD de muchos enteros arbitrariamente.

Descripción

Procedimiento

El algoritmo euclidiano procede en una serie de pasos, y la salida de cada paso se usa como entrada para el siguiente. Realice un seguimiento de los pasos con un contador de enteros k, de modo que el paso inicial corresponda a k = 0, el siguiente paso a k = 1, y así sobre.

Cada paso comienza con dos restos no negativos r_k−2 y r_k−1, con r_k−2 > r_k−1. El paso kth realiza una división con resto para encontrar el cociente q_k y el resto r _k de modo que:

r_{k}geq 0.}" xmlns="http://www.w3.org/1998/Math/MathML">rk− − 2=qkrk− − 1+rkconrk− − 1■rk≥ ≥ 0.{displaystyle r_{k-2}=q_{k}r_{k-1}+r_{k} {fnMicrosoft Sans Serif} r_{k-1} {k}geq 0.}r_{k}geq 0.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/931e08680c76a451882e84fc8607c38acf26696e" style="vertical-align: -0.671ex; width:39.904ex; height:2.509ex;"/>

Es decir, los múltiplos del número menor r_k−1 se restan del número mayor r _k−2 hasta que el resto r_k sea menor que r _k−1. Luego, el algoritmo continúa con el paso (k+1) que comienza con r_k−1 y r_k.

En el paso inicial k = 0, los residuos se establecen en r₋₂ = a y r₋₁ = b, los números para los que se busca el GCD. En el siguiente paso k = 1, los restos son r₋₁ = b y el resto r₀ del paso inicial, y así sucesivamente. El algoritmo procede en una secuencia de ecuaciones.

{displaystyle {begin{aligned}a&=q_{0}b+r_{0}\b&=q_{1}r_{0}+r_{1}\r_{0}&=q_{2}r_{1}+r_{2}\r_{1}&=q_{3}r_{2}+r_{3}\&,,,vdots end{aligned}}}

No es necesario modificar el algoritmo si a < b: en ese caso, el cociente inicial es q₀ = 0, el primer residuo es r₀ = a, y en adelante r_k−2 > r_k−1 para todo k ≥ 1.

Puesto que los restos son enteros no negativos que disminuyen con cada paso, la secuencia $r_{0}>r_{1}>r_{2}>cdots geq 0}" xmlns="http://www.w3.org/1998/Math/MathML">r− − 1■r0■r1■r2■⋯ ⋯ ≥ ≥ 0{displaystyle r_{-1} confíar_{0} confíar_{1} {2} títulocdots geq 0}r_{0}>r_{1}>r_{2}>cdots geq 0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/12c8babf4858787c7388de2049d41249802cd9ce" style="vertical-align: -0.671ex; width:29.068ex; height:2.509ex;"/>$ no puede ser infinito, por lo que el algoritmo finalmente debe dejar de producir el siguiente paso; pero el algoritmo de división siempre puede proceder a la (N+1) paso proporcionado r_N ■ 0. Por lo tanto el algoritmo debe eventualmente producir un cero restante r_N = 0. El último no cero restante es el mayor divisor común a y b:

${displaystyle r_{N-1}=gcd(a,b).}$

Prueba de validez

La validez del algoritmo euclidiano puede probarse mediante un argumento de dos pasos. En el primer paso, el residuo final distinto de cero r_N−1 se muestra para dividir tanto a como b. Como es un divisor común, debe ser menor o igual que el máximo común divisor g. En el segundo paso, se muestra que cualquier divisor común de a y b, incluido g, debe dividir a r_N−1; por lo tanto, g debe ser menor o igual que r_N−1. Estas dos desigualdades opuestas implican r_N−1 = g.

Para demostrar que r_N−1 divide tanto a como b (el primer paso), r_N−1 divide a su predecesor r_N−2

r N -2 = q N r N -1

ya que el residuo final r_N es cero. r_N−1 también divide a su siguiente predecesor r_{N− 3}

r N -3 = q N -1 r N -2 + r N -1

porque divide ambos términos en el lado derecho de la ecuación. Iterando el mismo argumento, r_N−1 divide todos los restos anteriores, incluidos a y b . Ninguno de los restos anteriores r_N−2, r_{N −3}, etc. divide a y b, ya que dejan resto. Dado que r_N−1 es un divisor común de a y b, r_N−1 ≤ g.

En el segundo paso, cualquier número natural c que divide tanto a como b (en otras palabras, cualquier divisor común de a y b) divide los residuos r_k. Por definición, a y b se pueden escribir como múltiplos de c: a = mc y b = nc, donde m y n son números naturales. Por lo tanto, c divide el residuo inicial r₀, ya que r₀ = a − q₀b = mc − q ₀nc = (m − q₀n)c. Un argumento análogo muestra que c también divide los residuos subsiguientes r₁, r₂, etc. Por lo tanto, el máximo común divisor g debe dividir a r_N−1, lo que implica que g ≤ r_N−1. Dado que la primera parte del argumento mostraba lo contrario (r_N−1 ≤ g), se sigue que g = r_N−1. Por lo tanto, g es el máximo común divisor de todos los pares siguientes:

g = gcd(a, b . b, r 0 . r 0, r 1) =... = gcd(r N -2, r N -1) r N -1 .

Ejemplo resuelto

Animación basada en la resta del algoritmo de Euclidean. El rectángulo inicial tiene dimensiones a= 1071 y b= 462. Plazas de tamaño 462×462 se colocan dentro de él dejando un rectángulo 462×147. Este rectángulo está teñido con 147×147 cuadrados hasta que se deja un rectángulo 21×147, que a su vez está teñido con 21×21 cuadrados, sin dejar ningún área descubierta. El tamaño cuadrado más pequeño, 21, es el GCD de 1071 y 462.

A modo de ilustración, el algoritmo euclidiano se puede usar para encontrar el máximo común divisor de a = 1071 y b = 462. Para comenzar, se restan múltiplos de 462 de 1071 hasta que el resto sea menor que 462. Se pueden restar dos múltiplos de este tipo (q₀ = 2), dejando un resto de 147:

1071 = 2 \times 462 + 147.

Luego se restan múltiplos de 147 de 462 hasta que el resto sea menor que 147. Se pueden restar tres múltiplos (q₁ = 3), dejando un resto de 21:

462 = 3 \times 147 + 21.

Luego se restan múltiplos de 21 de 147 hasta que el resto sea menor que 21. Se pueden restar siete múltiplos (q₂ = 7), sin dejar resto:

147 = 7 \times 21 + 0.

Dado que el último resto es cero, el algoritmo termina con 21 como el máximo común divisor de 1071 y 462. Esto concuerda con el mcd(1071, 462) encontrado por la factorización prima anterior. En forma tabular, los pasos son:

Paso k	Ecuación	Quotient and remainder
0	$1071 = q 0 462 + r 0$	$q 0 = 2$ y $r 0 = 147$
1	$462 = q 1 147 + r 1$	$q 1 = 3$ y $r 1 = 21$
2	$147 = q 2 21 + r 2$	$q 2 = 7$ y $r 2 = 0$ ; termina el algoritmo

Visualización

El algoritmo euclidiano se puede visualizar en términos de la analogía de mosaico dada anteriormente para el máximo común divisor. Supongamos que deseamos cubrir un rectángulo a-by-b exactamente con mosaicos cuadrados, donde a es el mayor de los dos números. Primero intentamos teselar el rectángulo usando mosaicos cuadrados b-by-b; sin embargo, esto deja un rectángulo residual r₀-by-b hasta que r₀ < b. Luego intentamos teselar el rectángulo residual con mosaicos cuadrados r₀-by-r₀. Esto deja un segundo rectángulo residual r₁-por-r₀, que intentamos colocar en mosaico usando r₁-por-r₁ fichas cuadradas, y así sucesivamente. La secuencia finaliza cuando no queda ningún rectángulo residual, es decir, cuando las fichas cuadradas cubren exactamente el rectángulo residual anterior. La longitud de los lados del mosaico cuadrado más pequeño es el MCD de las dimensiones del rectángulo original. Por ejemplo, el mosaico cuadrado más pequeño de la figura adyacente mide 21 por 21 (se muestra en rojo) y 21 es el GCD de 1071 y 462, las dimensiones del rectángulo original (se muestra en verde).

División euclidiana

En cada paso k, el algoritmo euclidiano calcula un cociente q_k y un resto r _k de dos números r_k−1 y r_k−2

r k -2 = q k r k -1 + r k

donde r_k no es negativo y es estrictamente menor que el valor absoluto de r_k−1. El teorema que subyace a la definición de la división euclidiana asegura que tal cociente y resto siempre existen y son únicos.

En la versión original del algoritmo de Euclid, el cociente y el resto se encuentran mediante restas repetidas; es decir, r_k−1 se resta de r_{k −2} repetidamente hasta que el resto r_k sea menor que r_k−1. Después de eso r_k y r_k−1 se intercambian y el proceso se itera. La división euclidiana reduce todos los pasos entre dos intercambios en un solo paso, por lo que es más eficiente. Además, los cocientes no son necesarios, por lo que se puede reemplazar la división euclidiana por la operación módulo, que da solo el resto. Por lo tanto, la iteración del algoritmo euclidiano se vuelve simplemente

r k = r k -2 mod r k -1 .

Implementaciones

Las implementaciones del algoritmo pueden expresarse en pseudocódigo. Por ejemplo, la versión basada en divisiones puede programarse como

función gcd(a, b)
 mientras b ل 0
t:= b
b:= a mod b
a:= t
 retorno a

Al comienzo de la késima iteración, la variable b contiene el último resto r_k−1, mientras que la variable a contiene su predecesora, r_k−2. El paso b:= a mod b es equivalente a la fórmula de recurrencia anterior r_k ≡ r_k−2 modificación r_k−1. La variable temporal t contiene el valor de r_k−1 mientras que el resto siguiente r_k está siendo calculado. Al final de la iteración del bucle, la variable b contiene el resto r_k, mientras que la variable a tiene su predecesor, r_k−1.

(Si se permiten entradas negativas, o si la función mod puede devolver valores negativos, la última línea debe cambiarse a return max(a, −a).)

En la versión basada en restas, que era la versión original de Euclid, el cálculo del resto (b:= a mod b) se reemplaza por restas repetidas. Al contrario de la versión basada en división, que funciona con números enteros arbitrarios como entrada, la versión basada en resta supone que la entrada consiste en números enteros positivos y se detiene cuando a = b:

función gcd(a, b)
 mientras a
 si a
a:= a − b
 másb:= b - a
 retorno a

Las variables a y b se alternan manteniendo los residuos anteriores r_k−1 y r_k−2. Suponga que a es mayor que b al comienzo de una iteración; entonces a es igual a r_k−2, ya que r_k−2 > r_k−1. Durante la iteración del bucle, a se reduce en múltiplos del resto anterior b hasta que a es menor que b. Entonces a es el resto siguiente r_k. Entonces b se reduce por múltiplos de a hasta que vuelve a ser menor que a, dando el resto siguiente r_k+1, y así sucesivamente.

La versión recursiva se basa en la igualdad de los MCD de residuos sucesivos y la condición de parada gcd(r_N−1, 0) = r_N−1.

función gcd(a, b)
 si b = 0
 retorno a
 más retorno gcd(b, a mod b)

(Como arriba, si se permiten entradas negativas, o si la función mod puede devolver valores negativos, la instrucción "return a" debe ser cambiado a "retorno máximo(a, −a)").

A modo ilustrativo, mcd(1071, 462) se calcula a partir del equivalente mcd(462, 1071 mod 462) = mcd(462, 147). El último GCD se calcula a partir de gcd(147, 462 mod 147) = gcd(147, 21), que a su vez se calcula a partir de mcd(21, 147 mod 21) = gcd(21, 0) = 21.

Método de los residuos absolutos mínimos

En otra versión del algoritmo de Euclides, el cociente en cada paso se incrementa en uno si el resto negativo resultante es menor en magnitud que el resto positivo típico. Anteriormente, la ecuación

r k -2 = q k r k -1 + r k

supuso que $| r k -1 | > r k > 0$ . Sin embargo, se puede calcular un resto negativo alternativo $e k$ :

r k -2 = q k + 1) r k -1 + e k

si $r k -1 > 0$ o

r k -2 = q k -1) r k -1 + e k

si $r k -1 < 0$ .

Si $r k$ se reemplaza por $e k .$ cuando $| e k | < | r k |$ , entonces se obtiene una variante del algoritmo euclidiano tal que

Silencio r k Ø \leq latitud r k -1 confidencialidad / 2

en cada paso.

Leopold Kronecker ha demostrado que esta versión requiere los pocos pasos de cualquier versión del algoritmo de Euclid. Más generalmente, se ha demostrado que, por cada número de entradas a y b, el número de pasos es mínimo si y sólo si $q k$ es elegido para que $<math alttext="{displaystyle left|{frac {r_{k+1}}{r_{k}}}right|Silenciork+1rkSilencio.1φ φ ♪ ♪ 0.618,{displaystyle lefttención{frac {fnK}} {fn}}}derecho] }sim 0.618,}<img alt="left|{frac {r_{k+1}}{r_{k}}}right|$ Donde $varphi$ es la relación de oro.

Desarrollo histórico

"Depiction of Euclid as a bearded man holding a pair of dividers to a tablet."

El algoritmo de Euclidean probablemente fue inventado antes de Euclid, representado aquí sosteniendo una brújula en una pintura de alrededor de 1474.

El algoritmo euclidiano es uno de los algoritmos más antiguos de uso común. Aparece en los Elementos de Euclides (c. 300 a. C.), específicamente en el Libro 7 (Proposiciones 1–2) y el Libro 10 (Proposiciones 2–3). En el Libro 7, el algoritmo está formulado para números enteros, mientras que en el Libro 10, está formulado para longitudes de segmentos de línea. (En el uso moderno, uno diría que fue formulado allí para números reales. Pero las longitudes, áreas y volúmenes, representados como números reales en el uso moderno, no se miden en las mismas unidades y no existe una unidad natural de longitud, área, o volumen; el concepto de números reales era desconocido en ese momento.) El último algoritmo es geométrico. El MCD de dos longitudes a y b corresponde a la mayor longitud g que mide a y b uniformemente; en otras palabras, las longitudes a y b son múltiplos enteros de la longitud g.

El algoritmo probablemente no fue descubierto por Euclid, quien recopiló resultados de matemáticos anteriores en sus Elementos. El matemático e historiador B. L. van der Waerden sugiere que el Libro VII se deriva de un libro de texto sobre teoría de números escrito por matemáticos de la escuela de Pitágoras. El algoritmo probablemente fue conocido por Eudoxo de Cnido (alrededor del 375 a. C.). El algoritmo puede incluso ser anterior a Eudoxo, a juzgar por el uso del término técnico ἀνθυφαίρεσις (anthyphairesis, sustracción recíproca) en obras de Euclides y Aristóteles.

Siglos más tarde, el algoritmo de Euclides se descubrió de forma independiente tanto en India como en China, principalmente para resolver las ecuaciones diofánticas que surgieron en astronomía y hacer calendarios precisos. A finales del siglo V, el matemático y astrónomo indio Aryabhata describió el algoritmo como el "pulverizador", quizás debido a su eficacia para resolver ecuaciones diofánticas. Aunque ya se había descrito un caso especial del teorema chino del resto en el libro chino Sunzi Suanjing, la solución general fue publicada por Qin Jiushao en su libro de 1247 Shushu Jiuzhang (數書九章 Tratado de matemáticas en nueve secciones). El algoritmo euclidiano se describió por primera vez numéricamente y se popularizó en Europa en la segunda edición de los Problèmes plaisants et délectables de Bachet (Problemas placenteros y placenteros, 1624). En Europa, también se utilizó para resolver ecuaciones diofánticas y en el desarrollo de fracciones continuas. El algoritmo euclidiano extendido fue publicado por el matemático inglés Nicholas Saunderson, quien lo atribuyó a Roger Cotes como un método para calcular fracciones continuas de manera eficiente.

En el siglo XIX, el algoritmo euclidiano condujo al desarrollo de nuevos sistemas numéricos, como los enteros gaussianos y los enteros de Eisenstein. En 1815, Carl Gauss usó el algoritmo euclidiano para demostrar la factorización única de los enteros gaussianos, aunque su trabajo se publicó por primera vez en 1832. Gauss mencionó el algoritmo en sus Disquisitiones Arithmeticae (publicado en 1801), pero solo como un Método para fracciones continuas. Peter Gustav Lejeune Dirichlet parece haber sido el primero en describir el algoritmo de Euclides como la base de gran parte de la teoría de números. Lejeune Dirichlet señaló que muchos resultados de la teoría de números, como la factorización única, serían válidos para cualquier otro sistema de números al que se pudiera aplicar el algoritmo euclidiano. Las conferencias de Lejeune Dirichlet sobre teoría de números fueron editadas y ampliadas por Richard Dedekind, quien usó el algoritmo de Euclides para estudiar los números enteros algebraicos, un nuevo tipo general de número. Por ejemplo, Dedekind fue el primero en demostrar el teorema de los dos cuadrados de Fermat utilizando la factorización única de los enteros gaussianos. Dedekind también definió el concepto de dominio euclidiano, un sistema numérico en el que se puede definir una versión generalizada del algoritmo euclidiano (como se describe a continuación). En las últimas décadas del siglo XIX, el algoritmo euclidiano fue gradualmente eclipsado por la teoría más general de los ideales de Dedekind.

"[El algoritmo de Euclidean] es el abuelo de todos los algoritmos, porque es el algoritmo notrivial más antiguo que ha sobrevivido hasta el día actual."

Donald Knuth, The Art of Computer Programming, Vol. 2: Algorithms seminumerical, 2a edición (1981), pág. 318.

En el siglo XIX se desarrollaron otras aplicaciones del algoritmo de Euclides. En 1829, Charles Sturm demostró que el algoritmo era útil en el método de cadena de Sturm para contar las raíces reales de polinomios en cualquier intervalo dado.

El algoritmo euclidiano fue el primer algoritmo de relación de enteros, que es un método para encontrar relaciones de enteros entre números reales proporcionales. Se han desarrollado varios algoritmos novedosos de relación de enteros, como el algoritmo de Helaman Ferguson y R.W. Forcade (1979) y el algoritmo LLL.

En 1969, Cole y Davie desarrollaron un juego para dos jugadores basado en el algoritmo euclidiano, llamado El juego de Euclides, que tiene una estrategia óptima. Los jugadores comienzan con dos montones de piedras a y b. Los jugadores se turnan para quitar m múltiplos de la pila más pequeña de la más grande. Por lo tanto, si las dos pilas consisten en piedras x e y, donde x es mayor que y, la siguiente el jugador puede reducir la pila más grande de x piedras a x − mis piedras, siempre que la última sea un número entero no negativo. El ganador es el primer jugador en reducir una pila a cero piedras.

Aplicaciones matemáticas

Identidad de Bézout

La identidad de Bézout establece que el máximo común divisor g de dos enteros a y b se puede representar como una suma lineal de los dos números originales a y b. En otras palabras, siempre es posible encontrar números enteros s y t tales que g = sa + tb.

Los enteros s y t se pueden calcular a partir de los cocientes q₀, q₁, etc. invirtiendo el orden de las ecuaciones en el algoritmo de Euclides. Comenzando con la penúltima ecuación, g se puede expresar en términos del cociente q_N−1 y los dos restos anteriores, r_N−2 y r_N−3:

g = r N -1 = r N -3 - q N -1 r N -2 .

Esos dos residuos también se pueden expresar en términos de sus cocientes y residuos anteriores,

r N -2 = r N -4 - q N -2 r N -3

r N -3 = r N; 5 - - q N -3 r N -4 .

Sustituyendo estas fórmulas por r_N−2 y r_N−3 en la primera ecuación produce g como una suma lineal de los residuos r_N−4 y r_N−5. El proceso de sustitución de residuos por fórmulas que involucran a sus predecesores puede continuar hasta que se alcancen los números originales a y b:

r 2 = r 0 - q 2 r 1

r 1 = b - q 1 r 0

r 0 = a - q 0 b .

Después de sustituir todos los residuos r₀, r₁, etc., la ecuación final expresa g como una suma lineal de a y b, de modo que g = sa + tb.

El algoritmo euclidiano y, por lo tanto, la identidad de Bezout, se pueden generalizar al contexto de los dominios euclidianos.

Ideales principales y problemas relacionados

La identidad de Bézout proporciona otra definición del máximo común divisor g de dos números a y b. Considere el conjunto de todos los números ua + vb, donde u y v son dos enteros cualesquiera. Dado que tanto a como b son divisibles por g, todos los números del conjunto son divisibles por g. En otras palabras, cada número del conjunto es un múltiplo entero de g. Esto es cierto para todos los divisores comunes de a y b. Sin embargo, a diferencia de otros divisores comunes, el máximo común divisor es un miembro del conjunto; por la identidad de Bézout, elegir u = s y v = t da g. Un divisor común más pequeño no puede ser miembro del conjunto, ya que todos los miembros del conjunto deben ser divisibles por g. Por el contrario, cualquier múltiplo m de g se puede obtener eligiendo u = ms y v = mt, donde s y t son los números enteros de la identidad de Bézout. Esto se puede ver multiplicando la identidad de Bézout por m,

mg = msa + mtb .

Por lo tanto, el conjunto de todos los números ua + vb es equivalente al conjunto de múltiplos m de g. En otras palabras, el conjunto de todas las sumas posibles de múltiplos enteros de dos números (a y b) es equivalente al conjunto de múltiplos de mcd(a, b). Se dice que el GCD es el generador del ideal de a y b. Esta definición de GCD condujo a los conceptos algebraicos abstractos modernos de un ideal principal (un ideal generado por un solo elemento) y un dominio ideal principal (un dominio en el que cada ideal es un ideal principal).

Algunos problemas se pueden resolver usando este resultado. Por ejemplo, considere dos tazas de medir de volumen a y b. Al sumar o restar u múltiplos de la primera taza y v múltiplos de la segunda taza, cualquier volumen ua + vb se puede medir. Estos volúmenes son todos múltiplos de g = gcd(a, b).

Algoritmo euclidiano extendido

Los números enteros s y t de la identidad de Bézout se pueden calcular de manera eficiente utilizando el algoritmo euclidiano extendido. Esta extensión agrega dos ecuaciones recursivas al algoritmo de Euclides

s k = s k -2 - q k s k -1

t k = t k -2 - q k t k -1

con los valores iniciales

s -2 = 1, t -2 = 0

s -1 = 0, t -1 = 1.

Usando esta recursividad, los enteros s y t de Bézout están dados por s = s _N y t = t_N, donde N+1 es el paso en el que el algoritmo termina con r_N+1 = 0.

La validez de este enfoque puede demostrarse por inducción. Suponga que la fórmula de recurrencia es correcta hasta el paso k − 1 del algoritmo; en otras palabras, suponer que

r j = s j a + t j b

para todos los j menores que k. El paso késimo del algoritmo da la ecuación

r k = r k -2 - q k r k -1 .

Dado que se ha asumido que la fórmula de recurrencia es correcta para r_k−2 y r_k−1, pueden expresarse en términos de las correspondientes variables s y t

r k = s k -2 a + t k -2 b) - q k () s k -1 a + t k -1 b).

Al reorganizar esta ecuación se obtiene la fórmula de recurrencia para el paso k, según se requiera

r k = s k a + t k b = s k -2 - q k s k -1) a + t k -2 - q k t k -1) b .

Método matricial

Los enteros s y t también se pueden encontrar utilizando un método de matriz equivalente. La secuencia de ecuaciones del algoritmo de Euclides

{displaystyle {begin{aligned}a&=q_{0}b+r_{0}\b&=q_{1}r_{0}+r_{1}\&,,,vdots \r_{N-2}&=q_{N}r_{N-1}+0end{aligned}}}

puede escribirse como un producto de matrices de cociente de 2 por 2 que multiplican un vector de resto bidimensional

{displaystyle {begin{pmatrix}a\bend{pmatrix}}={begin{pmatrix}q_{0}&1\1&0end{pmatrix}}{begin{pmatrix}b\r_{0}end{pmatrix}}={begin{pmatrix}q_{0}&1\1&0end{pmatrix}}{begin{pmatrix}q_{1}&1\1&0end{pmatrix}}{begin{pmatrix}r_{0}\r_{1}end{pmatrix}}=cdots =prod _{i=0}^{N}{begin{pmatrix}q_{i}&1\1&0end{pmatrix}}{begin{pmatrix}r_{N-1}\0end{pmatrix}},.}

Sea M el producto de todas las matrices de cociente

mathbf {M} ={begin{pmatrix}m_{11}&m_{12}\m_{21}&m_{22}end{pmatrix}}=prod _{i=0}^{N}{begin{pmatrix}q_{i}&1\1&0end{pmatrix}}={begin{pmatrix}q_{0}&1\1&0end{pmatrix}}{begin{pmatrix}q_{1}&1\1&0end{pmatrix}}cdots {begin{pmatrix}q_{N}&1\1&0end{pmatrix}},.

Esto simplifica el algoritmo euclidiano a la forma

{begin{pmatrix}a\bend{pmatrix}}=mathbf {M} {begin{pmatrix}r_{N-1}\0end{pmatrix}}=mathbf {M} {begin{pmatrix}g\0end{pmatrix}},.

Para expresar g como una suma lineal de a y b, ambos lados de esta ecuación se pueden multiplicar por la inversa de la matriz M. El determinante de M es igual a (−1)^N+1, ya que es igual al producto de los determinantes de las matrices de cocientes, cada una de las cuales es negativo. Como el determinante de M nunca es cero, el vector de los residuos finales se puede resolver usando el inverso de M

{begin{pmatrix}g\0end{pmatrix}}=mathbf {M} ^{-1}{begin{pmatrix}a\bend{pmatrix}}=(-1)^{N+1}{begin{pmatrix}m_{22}&-m_{12}\-m_{21}&m_{11}end{pmatrix}}{begin{pmatrix}a\bend{pmatrix}},.

Dado que la ecuación superior da

g = (1)- N + 1 () m 22 a - m 12 b),

los dos enteros de la identidad de Bézout son s = (−1)^N+1m₂₂ y t = (−1)^Nm₁₂. El método matricial es tan eficiente como la recursividad equivalente, con dos multiplicaciones y dos sumas por paso del algoritmo euclidiano.

Lema de Euclides y factorización única

La identidad de Bézout es esencial para muchas aplicaciones del algoritmo de Euclides, como demostrar la factorización única de números en factores primos. Para ilustrar esto, suponga que un número L se puede escribir como un producto de dos factores u y v, es decir, L = uv. Si otro número w también divide a L pero es coprimo con u, entonces w debe dividir a v, por el siguiente argumento: si el máximo común divisor de u y w es 1, entonces los números enteros s y t se puede encontrar tal que

1 = su + # .

por la identidad de Bézout. Multiplicando ambos lados por v da la relación

v = Suv + Twv = SL + Twv .

Dado que w divide ambos términos en el lado derecho, también debe dividir el lado izquierdo, v. Este resultado se conoce como el lema de Euclides. Específicamente, si un número primo divide L, entonces debe dividir al menos un factor de L. Por el contrario, si un número w es coprimo para cada uno de una serie de números a₁, a₂,..., a_n, entonces w también es coprime para su producto, a₁ × a₂ ×... × a_n.

El lema de Euclides es suficiente para probar que todo número tiene una factorización única en números primos. Para ver esto, suponga lo contrario, que hay dos factorizaciones independientes de L en m y n factores primos, respectivamente

L = p 1 p 2 ... p m = q 1 q 2 ... q n .

Dado que cada número primo p divide L por suposición, también debe dividir uno de los factores q; dado que cada q también es primo, debe ser que p = q. La división iterativa por los factores p muestra que cada p tiene una contrapartida igual q; las dos factorizaciones primas son idénticas excepto por su orden. La factorización única de números en números primos tiene muchas aplicaciones en demostraciones matemáticas, como se muestra a continuación.

Ecuaciones diofánticas lineales

Parcela de una ecuación lineal de Diofantina, 9x+ 12Sí.= 483. Las soluciones se muestran como círculos azules.

Las ecuaciones diofánticas son ecuaciones en las que las soluciones están restringidas a números enteros; llevan el nombre del matemático alejandrino del siglo III Diofanto. Una típica ecuación diofántica lineal busca números enteros x e y tales que

ax + por = c

donde a, b y c son números enteros. Esto se puede escribir como una ecuación para x en aritmética modular:

ax ↑ c mod b .

Sea g el máximo común divisor de a y b. Ambos términos en ax + by son divisibles por g; por lo tanto, c también debe ser divisible por g, o la ecuación no tiene soluciones. Al dividir ambos lados por c/g, la ecuación se puede reducir a la identidad de Bezout

sa + tb = g

donde s y t se pueden encontrar mediante el algoritmo euclidiano extendido. Esto proporciona una solución a la ecuación diofántica, x₁ = s (c/g) y y₁ = t (c/g).

En general, una ecuación diofántica lineal no tiene soluciones o tiene un número infinito de soluciones. Para encontrar este último, considere dos soluciones, (x₁, y₁) y (x ₂, y₂), donde

ax 1 + por 1 = c = ax 2 + por 2

o equivalente

a () x 1 - x 2) b () Sí. 2 - Sí. 1).

Por lo tanto, la diferencia más pequeña entre dos soluciones x es b/g, mientras que la diferencia más pequeña entre dos y soluciones es a/g. Por lo tanto, las soluciones se pueden expresar como

x = x 1 - bu / g

Sí. = Sí. 1 + au / g

Al permitir que u varíe entre todos los enteros posibles, se puede generar una familia infinita de soluciones a partir de una sola solución (x₁, y₁). Si se requiere que las soluciones sean números enteros positivos (x > 0, y > 0), solo se puede obtener un número finito de soluciones. posible. Esta restricción sobre las soluciones aceptables permite que algunos sistemas de ecuaciones diofánticas con más incógnitas que ecuaciones tengan un número finito de soluciones; esto es imposible para un sistema de ecuaciones lineales cuando las soluciones pueden ser cualquier número real (ver Sistema indeterminado).

Inversos multiplicativos y el algoritmo RSA

Un campo finito es un conjunto de números con cuatro operaciones generalizadas. Las operaciones se denominan suma, resta, multiplicación y división y tienen sus propiedades habituales, como conmutatividad, asociatividad y distributividad. Un ejemplo de un campo finito es el conjunto de 13 números {0, 1, 2,..., 12} usando aritmética modular. En este campo, los resultados de cualquier operación matemática (suma, resta, multiplicación o división) se reducen al módulo 13; es decir, se suman o restan múltiplos de 13 hasta que el resultado se sitúa dentro del rango de 0 a 12. Por ejemplo, el resultado de 5 × 7 = 35 mod 13 = 9. Dichos campos finitos se pueden definir para cualquier primo p; utilizando definiciones más sofisticadas, también se pueden definir para cualquier potencia m de un número primo p^m. Los campos finitos a menudo se denominan campos de Galois y se abrevian como GF(p) o GF(p^m).

En tal campo con m números, cada elemento distinto de cero a tiene un inverso multiplicativo modular único, a⁻¹ tal que aa⁻¹ = a⁻¹a ≡ 1 mod m. Este inverso se puede encontrar resolviendo la ecuación de congruencia ax ≡ 1 mod m, o la ecuación diofántica lineal equivalente

ax + # = 1.

Esta ecuación se puede resolver mediante el algoritmo euclidiano, como se describe anteriormente. Encontrar inversos multiplicativos es un paso esencial en el algoritmo RSA, que es muy utilizado en el comercio electrónico; específicamente, la ecuación determina el número entero utilizado para descifrar el mensaje. Aunque el algoritmo RSA usa anillos en lugar de campos, el algoritmo euclidiano aún se puede usar para encontrar un inverso multiplicativo donde exista. El algoritmo euclidiano también tiene otras aplicaciones en códigos de corrección de errores; por ejemplo, se puede utilizar como una alternativa al algoritmo de Berlekamp-Massey para decodificar códigos BCH y Reed-Solomon, que se basan en campos de Galois.

Teorema del resto chino

El algoritmo de Euclides también se puede usar para resolver múltiples ecuaciones diofánticas lineales. Tales ecuaciones surgen en el teorema chino del resto, que describe un método novedoso para representar un número entero x. En lugar de representar un número entero por sus dígitos, puede representarse por sus residuos x_i módulo un conjunto de N números coprimos m_i:

{displaystyle {begin{aligned}x_{1}&equiv x{pmod {m_{1}}}\x_{2}&equiv x{pmod {m_{2}}}\&,,,vdots \x_{N}&equiv x{pmod {m_{N}}},.end{aligned}}}

El objetivo es determinar x a partir de sus N restos x_i. La solución es combinar las múltiples ecuaciones en una sola ecuación diofántica lineal con un módulo mucho mayor M que es el producto de todos los módulos individuales m_i, y define M_i como

{displaystyle M_{i}={frac {M}{m_{i}}}.}

Así, cada M_i es el producto de todos los módulos excepto m_i. La solución depende de encontrar N nuevos números h_i tales que

{displaystyle M_{i}h_{i}equiv 1{pmod {m_{i}}},.}

Con estos números h_i, cualquier número entero x se puede reconstruir a partir de sus restos x _i por la ecuación

{displaystyle xequiv (x_{1}M_{1}h_{1}+x_{2}M_{2}h_{2}+cdots +x_{N}M_{N}h_{N}){pmod {M}},.}

Dado que estos números h_i son los inversos multiplicativos de la M_i, se pueden encontrar usando el algoritmo de Euclid como se describe en la subsección anterior.

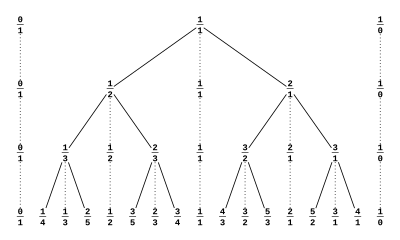
Árbol de popa-Brocot

El algoritmo euclidiano se puede utilizar para organizar el conjunto de todos los números racionales positivos en un árbol de búsqueda binario infinito, denominado árbol de Stern-Brocot. El número 1 (expresado como una fracción 1/1) se coloca en la raíz del árbol, y la ubicación de cualquier otro número a/b se puede encontrar calculando gcd(a,b) utilizando la forma original del algoritmo euclidiano, en el que cada paso reemplaza el mayor de los dos números dados por su diferencia con el número menor (no su resto), deteniéndose cuando se alcanzan dos números iguales. Un paso del algoritmo euclidiano que reemplaza el primero de los dos números corresponde a un paso en el árbol desde un nodo a su hijo derecho, y un paso que reemplaza el segundo de los dos números corresponde a un paso en el árbol desde un nodo a su hijo izquierdo. La secuencia de pasos construida de esta manera no depende de si a/b se da en términos mínimos, y forma un camino desde la raíz hasta un nodo que contiene el número a/b. Este hecho se puede usar para probar que cada número racional positivo aparece exactamente una vez en este árbol.

Por ejemplo, 3/4 se puede encontrar comenzando en la raíz, yendo hacia la izquierda una vez y luego hacia la derecha dos veces:

El árbol Stern-Brocot, y las secuencias Stern-Brocot de orden i para i = 1, 2, 3, 4

{displaystyle {begin{aligned}&gcd(3,4)&leftarrow \={}&gcd(3,1)&rightarrow \={}&gcd(2,1)&rightarrow \={}&gcd(1,1).end{aligned}}}

El algoritmo euclidiano tiene casi la misma relación con otro árbol binario de los números racionales llamado árbol de Calkin-Wilf. La diferencia es que la ruta se invierte: en lugar de producir una ruta desde la raíz del árbol hasta un objetivo, produce una ruta desde el objetivo hasta la raíz.

Fracciones continuas

El algoritmo euclidiano tiene una estrecha relación con las fracciones continuas. La secuencia de ecuaciones se puede escribir en la forma

{displaystyle {begin{aligned}{frac {a}{b}}&=q_{0}+{frac {r_{0}}{b}}\{frac {b}{r_{0}}}&=q_{1}+{frac {r_{1}}{r_{0}}}\{frac {r_{0}}{r_{1}}}&=q_{2}+{frac {r_{2}}{r_{1}}}\&,,,vdots \{frac {r_{k-2}}{r_{k-1}}}&=q_{k}+{frac {r_{k}}{r_{k-1}}}\&,,,vdots \{frac {r_{N-2}}{r_{N-1}}}&=q_{N},.end{aligned}}}

El último término del lado derecho siempre es igual al inverso del lado izquierdo de la siguiente ecuación. Por lo tanto, las dos primeras ecuaciones se pueden combinar para formar

{displaystyle {frac {a}{b}}=q_{0}+{cfrac {1}{q_{1}+{cfrac {r_{1}}{r_{0}}}}},.}

La tercera ecuación se puede usar para sustituir el término denominador r₁/r₀, dando como resultado

{displaystyle {frac {a}{b}}=q_{0}+{cfrac {1}{q_{1}+{cfrac {1}{q_{2}+{cfrac {r_{2}}{r_{1}}}}}}},.}

La razón final de los residuos r_k/r_k−1 siempre se puede reemplazar usando la siguiente ecuación de la serie, hasta la ecuación final. El resultado es una fracción continua.

{displaystyle {frac {a}{b}}=q_{0}+{cfrac {1}{q_{1}+{cfrac {1}{q_{2}+{cfrac {1}{ddots +{cfrac {1}{q_{N}}}}}}}}}=[q_{0};q_{1},q_{2},ldotsq_{N}],.}

En el ejemplo resuelto anterior, se calculó el mcd(1071, 462), y los cocientes q_k fueron 2, 3 y 7, respectivamente. Por tanto, la fracción 1071/462 puede escribirse

{displaystyle {frac {1071}{462}}=2+{cfrac {1}{3+{cfrac {1}{7}}}}=[2;3,7]}

como se puede confirmar por cálculo.

Algoritmos de factorización

Calcular un máximo común divisor es un paso esencial en varios algoritmos de factorización de enteros, como el algoritmo rho de Pollard, el algoritmo de Shor, el método de factorización de Dixon y la factorización de la curva elíptica de Lenstra. El algoritmo euclidiano se puede usar para encontrar este GCD de manera eficiente. La factorización de fracciones continuas utiliza fracciones continuas, que se determinan mediante el algoritmo de Euclides.

Eficiencia algorítmica

Número de pasos en el algoritmo de Euclidean para gcd(x,Sí.). Puntos más ligeros (rojo y amarillo) indican relativamente pocos pasos, mientras que puntos más oscuros (violeta y azul) indican más pasos. El área oscura más grande sigue la línea Sí. = ⋅x, donde CCPR es la relación de oro.

La eficiencia computacional del algoritmo de Euclid se ha estudiado a fondo. Esta eficiencia se puede describir por el número de pasos de división que requiere el algoritmo, multiplicado por el gasto computacional de cada paso. El primer análisis conocido del algoritmo de Euclides se debe a A. A. L. Reynaud en 1811, quien demostró que el número de pasos de división en la entrada (u, v) está acotado por v; más tarde lo mejoró a v/2 + 2. Más tarde, en 1841, P. J. E. Finck demostró que el número de pasos de división es como máximo 2 log₂ v + 1 y, por lo tanto, el algoritmo de Euclid se ejecuta en un polinomio de tiempo en el tamaño de la entrada. Émile Léger, en 1837, estudió el peor de los casos, que es cuando las entradas son números de Fibonacci consecutivos. El análisis de Finck fue perfeccionado por Gabriel Lamé en 1844, quien demostró que el número de pasos requeridos para completar nunca es más de cinco veces el número h de dígitos en base 10 del número más pequeño b.

En el modelo de costo uniforme (adecuado para analizar la complejidad del cálculo de gcd en números que caben en una sola palabra de máquina), cada paso del algoritmo requiere un tiempo constante, y el análisis de Lamé implica que el tiempo total de ejecución es también O(h). Sin embargo, en un modelo de cómputo adecuado para el cómputo con números más grandes, el gasto computacional de un cómputo de un solo resto en el algoritmo puede ser tan grande como O(h²). En este caso, el tiempo total para todos los pasos del algoritmo se puede analizar usando una serie telescópica, mostrando que también es O(h²). Se pueden utilizar técnicas algorítmicas modernas basadas en el algoritmo de Schönhage-Strassen para la multiplicación rápida de enteros para acelerar esto, lo que lleva a algoritmos cuasilineales para el GCD.

Número de pasos

El número de pasos para calcular el MCD de dos números naturales, a y b, se puede denotar con T( a, b). Si g es el GCD de a y b, entonces a = mg y b = ng para dos números coprimos m y n. Después

T () a, b) T () m, n)

como puede verse dividiendo todos los pasos del algoritmo euclidiano por g. Por el mismo argumento, el número de pasos sigue siendo el mismo si a y b se multiplican por un factor común w: T(a, b) = T(wa, wb). Por lo tanto, el número de pasos T puede variar drásticamente entre pares de números vecinos, como T(a, b) y T(a, b + 1), según el tamaño de los dos GCD.

La naturaleza recursiva del algoritmo euclidiano da otra ecuación

T () a, b) = 1 + T () b, r 0) = 2 + T () r 0, r 1) = N + T () r N -2, r N -1) N + 1

donde T(x, 0) = 0 por suposición.

En el peor de los casos

Si el algoritmo euclidiano requiere N pasos para un par de números naturales a > b > 0, los valores más pequeños de a y b para los que esto es cierto son los números de Fibonacci F_N+2 y F_N+1, respectivamente. Más precisamente, si el algoritmo euclidiano requiere N pasos para el par a > b, entonces uno tiene a ≥ F_N+2 y b ≥ F_N+1. Esto se puede demostrar por inducción. Si N = 1, b divide a sin resto; los números naturales más pequeños para los que esto es cierto son b = 1 y a = 2, que son F₂ y F₃, respectivamente. Ahora suponga que el resultado es válido para todos los valores de N hasta M − 1. El primer paso del algoritmo de pasos M es a = q₀b + r₀, y el algoritmo euclidiano requiere M − 1 pasos para el par b > r₀. Por hipótesis de inducción, se tiene b ≥ F_M+1 y r₀ ≥ F_M. Por lo tanto, a = q₀b + r₀ ≥ b + r₀ ≥ F_M+1 + M_M = M_M+2, que es la desigualdad buscada. Esta prueba, publicada por Gabriel Lamé en 1844, representa el comienzo de la teoría de la complejidad computacional, y también la primera aplicación práctica de los números de Fibonacci.

Este resultado es suficiente para mostrar que el número de pasos en el algoritmo de Euclides nunca puede ser más de cinco veces el número de sus dígitos (base 10). Porque si el algoritmo requiere N pasos, entonces b es mayor o igual que F_{N+ 1} que a su vez es mayor o igual que φ^N−1, donde φ es la proporción áurea. Dado que b ≥ φ^N−1, entonces N − 1 ≤ log_φb. Desde log₁₀φ > 1/5, (N − 1)/5 < log₁₀φ log_φb = log_{10</sub b. Así, N ≤ 5 log₁₀b. Por lo tanto, el algoritmo euclidiano siempre necesita divisiones menores que O(h), donde h es el número de dígitos en el número menor b.}

Promedio

El número promedio de pasos tomados por el algoritmo euclidiano se ha definido de tres maneras diferentes. La primera definición es el tiempo promedio T(a) requerido para calcular el MCD de un número dado a y un número natural más pequeño b elegido con igual probabilidad entre los números enteros 0 a a − 1

<math alttext="{displaystyle T(a)={frac {1}{a}}sum _{0leq bT()a)=1a.. 0≤ ≤ b.aT()a,b).{displaystyle T(a)={frac {1}sum _{0leq b madea}T(a,b). }<img alt="{displaystyle T(a)={frac {1}{a}}sum _{0leq b

Sin embargo, dado que T(a, b) fluctúa drásticamente con el GCD de los dos números, la función promediada T (a) es igualmente "ruidoso".

Para reducir este ruido, se toma un segundo promedio τ(a) sobre todos los números coprimos con a

<math alttext="{displaystyle tau (a)={frac {1}{varphi (a)}}sum _{begin{smallmatrix}0leq b

τ τ ()a)=1φ φ ()a).. 0≤ ≤ b.agcd()a,b)=1T()a,b).{displaystyle tau (a)={frac {1}{varphi (a)}sum _{begin{smallmatrix}0leq b madeagcd(a,b)=1end{smallmatrix}T(a,b). }<img alt="{displaystyle tau (a)={frac {1}{varphi (a)}}sum _{begin{smallmatrix}0leq b

Hay φ(a) enteros coprimos menores que a, donde φ es Euler' s función de paciente. Este promedio de tau crece suavemente con a

{displaystyle tau (a)={frac {12}{pi ^{2}}}ln 2ln a+C+O(a^{-1/6-varepsilon })}

siendo el error residual de orden a^{−(1/6) + ε}, donde ε es infinitesimal. La constante C en esta fórmula se llama constante de Porter y es igual a

{displaystyle C=-{frac {1}{2}}+{frac {6ln 2}{pi ^{2}}}left(4gamma -{frac {24}{pi ^{2}}}zeta '(2)+3ln 2-2right)approx 1.467}

donde γ es la constante de Euler-Mascheroni y ζ' es la derivada de la función zeta de Riemann. El coeficiente principal (12/π²) ln 2 se determinó mediante dos métodos independientes.

Dado que el primer promedio se puede calcular a partir del promedio tau sumando los divisores d de a

{displaystyle T(a)={frac {1}{a}}sum _{dmid a}varphi (d)tau (d)}

se puede aproximar mediante la fórmula

{displaystyle T(a)approx C+{frac {12}{pi ^{2}}}ln 2left(ln a-sum _{dmid a}{frac {Lambda (d)}{d}}right)}

donde Λ(d) es la función de Mangoldt.

Un tercer promedio Y(n) se define como el número medio de pasos necesarios cuando a y b se eligen aleatoriamente (con distribución uniforme) de 1 a n

{displaystyle Y(n)={frac {1}{n^{2}}}sum _{a=1}^{n}sum _{b=1}^{n}T(a,b)={frac {1}{n}}sum _{a=1}^{n}T(a).}

Al sustituir la fórmula aproximada de T(a) en esta ecuación se obtiene una estimación de Y(n)

{displaystyle Y(n)approx {frac {12}{pi ^{2}}}ln 2ln n+0.06.}

Gasto computacional por paso

En cada paso k del algoritmo euclidiano, el cociente q_k y el resto r _k se calculan para un par dado de enteros r_k−2 y r_k−1

r k -2 = q k r k -1 + r k .

El gasto computacional por paso está asociado principalmente con encontrar q_k, ya que el resto r_k se puede calcular rápidamente a partir de r_k−2, r_k−1 y q_k

r k = r k -2 - q k r k -1 .

El gasto computacional de dividir números de h bits se escala como O(h(ℓ+1)), donde ℓ es la longitud del cociente.

A modo de comparación, el algoritmo original basado en restas de Euclid puede ser mucho más lento. Una sola división entera es equivalente al cociente q del número de restas. Si la razón de a y b es muy grande, el cociente es grande y se requerirán muchas restas. Por otro lado, se ha demostrado que es muy probable que los cocientes sean números enteros pequeños. La probabilidad de un cociente dado q es aproximadamente ln|u/(u − 1)| donde u = (q + 1)². Por ejemplo, la probabilidad de un cociente de 1, 2, 3 o 4 es aproximadamente 41,5 %, 17,0 %, 9,3 % y 5,9 %, respectivamente. Dado que la operación de resta es más rápida que la división, particularmente para números grandes, el algoritmo de Euclides basado en la resta es competitivo con la versión basada en la división. Esto se aprovecha en la versión binaria del algoritmo de Euclides.

Combinar el número estimado de pasos con el gasto computacional estimado por paso muestra que el algoritmo de Euclides crece cuadráticamente (h²) con el número promedio de dígitos h en los dos números iniciales a y b. Sea h₀, h₁,..., h_N−1 representan el número de dígitos en los restos sucesivos r₀, r₁,..., r_N−1. Dado que el número de pasos N crece linealmente con h, el tiempo de ejecución está limitado por

<math alttext="{displaystyle O{Big (}sum _{i<N}h_{i}(h_{i}-h_{i+1}+2){Big)}subseteq O{Big (}hsum _{iO().. i.Nhi()hi− − hi+1+2))⊆ ⊆ O()h.. i.N()hi− − hi+1+2))⊆ ⊆ O()h()h0+2N))⊆ ⊆ O()h2).{displaystyle O{Big (}sum _{i donen}h_{i}-h_{i}-h_{i+1}+2){Big)}subseteq O{Big (}hsum _{i donen}(h_{i}-h_{i+1}+2){Big)}subseteq O(h_{0}+2N))subseteq O(h^{2}). }<img alt="{displaystyle O{Big (}sum _{i<N}h_{i}(h_{i}-h_{i+1}+2){Big)}subseteq O{Big (}hsum _{i

Métodos alternativos

El algoritmo de Euclides se usa ampliamente en la práctica, especialmente para números pequeños, debido a su simplicidad. A modo de comparación, se puede determinar la eficiencia de las alternativas al algoritmo de Euclides.

Un enfoque ineficiente para encontrar el MCD de dos números naturales a y b es calcular todos sus divisores comunes; el MCD es entonces el máximo común divisor. Los divisores comunes se pueden encontrar dividiendo ambos números por enteros sucesivos desde 2 hasta el número menor b. El número de pasos de este enfoque crece linealmente con b, o exponencialmente en el número de dígitos. Otro enfoque ineficiente es encontrar los factores primos de uno o ambos números. Como se indicó anteriormente, el GCD es igual al producto de los factores primos compartidos por los dos números a y b. Los métodos actuales para la descomposición en factores primos también son ineficientes; muchos sistemas criptográficos modernos incluso se basan en esa ineficiencia.

El algoritmo GCD binario es una alternativa eficiente que sustituye la división por operaciones más rápidas al explotar la representación binaria utilizada por las computadoras. Sin embargo, esta alternativa también escala como O(h²). Por lo general, es más rápido que el algoritmo euclidiano en computadoras reales, aunque se escala de la misma manera. Se puede obtener una eficiencia adicional examinando solo los primeros dígitos de los dos números a y b. El algoritmo binario se puede extender a otras bases (algoritmos k-arios), con aumentos de velocidad de hasta cinco veces. El algoritmo GCD de Lehmer utiliza el mismo principio general que el algoritmo binario para acelerar los cálculos de GCD en bases arbitrarias.

Un enfoque recursivo para enteros muy grandes (con más de 25 000 dígitos) conduce a algoritmos GCD de enteros cuasilineales, como los de Schönhage, Stehlé y Zimmermann. Estos algoritmos explotan la forma matricial 2×2 del algoritmo euclidiano anterior. Estos métodos cuasilineales generalmente escalan como O(h (log h)² (registro registro h)).

Generalizaciones

Aunque el algoritmo euclidiano se usa para encontrar el máximo común divisor de dos números naturales (enteros positivos), se puede generalizar a los números reales y a otros objetos matemáticos, como polinomios, enteros cuadráticos y cuaterniones de Hurwitz. En los últimos casos, el algoritmo euclidiano se usa para demostrar la propiedad crucial de la factorización única, es decir, que dichos números pueden factorizarse de manera única en elementos irreducibles, las contrapartes de los números primos. La factorización única es esencial para muchas pruebas de teoría de números.

Números racionales y reales

El algoritmo de Euclides se puede aplicar a números reales, como lo describe Euclides en el Libro 10 de sus Elementos. El objetivo del algoritmo es identificar un número real $g$ tal que dos números reales dados, $a$ y $b$ , son múltiplos enteros de él: $a = mg$ y $b = ng$ , donde $m$ y $n$ son números enteros. Esta identificación es equivalente a encontrar una relación entera entre los números reales $a$ y $b$ ; es decir, determina los números enteros $s$ y $t$ tal que $sa + tb = 0$ . Si tal ecuación es posible, a y b se denominan longitudes conmensurables; de lo contrario, son longitudes inconmensurables.

El algoritmo euclidiano de números reales difiere de su homólogo entero en dos aspectos. Primero, los residuos $r k$ son números reales, aunque los cocientes $q k$ son números enteros como antes. En segundo lugar, no se garantiza que el algoritmo termine en un número finito $N$ de pasos. Si es así, la fracción $a / b$ es un número racional, es decir, la razón de dos enteros

{displaystyle {frac {a}{b}}={frac {mg}{ng}}={frac {m}{n}},}

y se puede escribir como una fracción continua finita $[q 0; q 1, q 2,..., q N]$ . Si el algoritmo no se detiene, la fracción $a / b$ es un número irracional y puede describirse mediante un infinito continuo fracción $[q 0; q 1, q 2, \dots]$ . Ejemplos de fracciones continuas infinitas son la proporción áurea $φ = [1; 1, 1,...]$ y la raíz cuadrada de dos, $\sqrt 2 = [1; 2, 2,...]$ . Es poco probable que el algoritmo se detenga, ya que casi todas las proporciones $a / b$ de dos números reales son irracionales.

Una fracción continua infinita se puede truncar en un paso $k [q 0; q 1, q 2,..., q k]$ para producir una aproximación a $a / b$ eso mejora a medida que aumenta $k$ . La aproximación se describe mediante convergentes $m k / n k$ ; el numerador y los denominadores son coprimos y obedecen a la relación de recurrencia

{displaystyle {begin{aligned}m_{k}&=q_{k}m_{k-1}+m_{k-2}\n_{k}&=q_{k}n_{k-1}+n_{k-2},end{aligned}}}

donde $m -1 = n -2 = 1$ y $m -2 = n -1 = 0$ son los valores iniciales de la recursividad. El convergente $m k / n k$ es la mejor aproximación de número racional a $a / b$ con denominador n_k:

<math alttext="{displaystyle left|{frac {a}{b}}-{frac {m_{k}}{n_{k}}}right|Silencioab− − mknkSilencio.1nk2.{displaystyle lefttención{frac {a}{b}-{frac} Está bien. {1}{n_{k}}}}<img alt="{displaystyle left|{frac {a}{b}}-{frac {m_{k}}{n_{k}}}right|

Polinomios

Los polinomios en una sola variable x se pueden sumar, multiplicar y factorizar en polinomios irreducibles, que son los análogos de los números primos para los enteros. El polinomio máximo común divisor $g (x)$ de dos polinomios $a (x)$ y $b (x)$ es definido como el producto de sus polinomios irreducibles compartidos, que se pueden identificar utilizando el algoritmo de Euclides. El procedimiento básico es similar al de los números enteros. En cada paso $k$ , un polinomio cociente $q k (x)$ y un polinomio de resto $r k (x)$ se identifican para satisfacer la ecuación recursiva

{displaystyle r_{k-2}(x)=q_{k}(x)r_{k-1}(x)+r_{k}(x),}

donde $r -2 (x) = a (x)$ y $r -1 (x) = b (x)$ . Cada polinomio cociente se elige de modo que cada resto sea cero o tenga un grado menor que el grado de su predecesor: $grado[r k (x)] < grado[r k -1 (x)]$ . Dado que el grado es un número entero no negativo y que disminuye con cada paso, el algoritmo euclidiano concluye en un número finito de pasos. El último residuo distinto de cero es el máximo común divisor de los dos polinomios originales, $a (x)$ y $b (x)$ .

Por ejemplo, considere los dos polinomios cuarticos siguientes, cada uno de los cuales se factoriza en dos polinomios cuadráticos

{displaystyle {begin{aligned}a(x)&=x^{4}-4x^{3}+4x^{2}-3x+14=(x^{2}-5x+7)(x^{2}+x+2)qquad {text{and}}\b(x)&=x^{4}+8x^{3}+12x^{2}+17x+6=(x^{2}+7x+3)(x^{2}+x+2).end{aligned}}}

Dividir $a (x)$ entre $b (x)$ genera un resto $r 0 (x) = x 3 + (2/3) x 2 + (5/3) x - (2/3)$ . En el siguiente paso, $b (x)$ se divide por $r 0 (x)$ dando un resto $r 1 (x) = x 2 + x + 2$ . Finalmente, dividiendo $r 0 (x)$ por $r 1 (x)$ genera un resto cero, lo que indica que $r 1 (x)$ es el polinomio máximo común divisor de $a (x)$ y $b (x)$ , consistentes con su factorización.

Muchas de las aplicaciones descritas anteriormente para los números enteros se trasladan a los polinomios. El algoritmo euclidiano se puede utilizar para resolver ecuaciones diofánticas lineales y problemas de residuos chinos para polinomios; También se pueden definir fracciones continuas de polinomios.

El algoritmo polinomial euclidiano tiene otras aplicaciones, como las cadenas de Sturm, un método para contar los ceros de un polinomio que se encuentran dentro de un intervalo real dado. Esto, a su vez, tiene aplicaciones en varias áreas, como el criterio de estabilidad de Routh-Hurwitz en la teoría de control.

Finalmente, los coeficientes de los polinomios no necesitan extraerse de números enteros, números reales o incluso de los números complejos. Por ejemplo, los coeficientes pueden extraerse de un campo general, como los campos finitos $GF(p)$ descritos anteriormente. Las conclusiones correspondientes sobre el algoritmo de Euclides y sus aplicaciones son válidas incluso para tales polinomios.

Enteros gaussianos

Distribución de primos gausianos

u + vi

en el plano complejo, con normas

u 2 + v 2

menos de 500

Los enteros gaussianos son números complejos de la forma $α = u + vi$ , donde $u$ y $v$ son números enteros ordinarios y $i$ es la raíz cuadrada de uno negativo. Al definir un análogo del algoritmo euclidiano, se puede demostrar que los enteros gaussianos son factorizables de manera única, según el argumento anterior. Esta factorización única es útil en muchas aplicaciones, como derivar todas las ternas de Pitágoras o probar el teorema de Fermat en sumas de dos cuadrados. En general, el algoritmo de Euclides es conveniente en tales aplicaciones, pero no es esencial; por ejemplo, los teoremas a menudo se pueden probar con otros argumentos.

El algoritmo euclidiano desarrollado para dos enteros gaussianos $α$ y $β$ es casi lo mismo que para los enteros ordinarios, pero difiere en dos aspectos. Como antes, establecemos $r -2 = α$ y $r -1 = β$ , y la tarea en cada paso $k$ es identificar un cociente $q k$ y un resto $r k$ tal que

{displaystyle r_{k}=r_{k-2}-q_{k}r_{k-1},}

donde cada resto es estrictamente más pequeño que su predecesor: $| r k | < | r k -1 |$ . La primera diferencia es que los cocientes y los residuos son enteros gaussianos y, por lo tanto, son números complejos. Los cocientes $q k$ generalmente se encuentran redondeando las partes reales y complejas de la exacta proporción (como el número complejo $α / β$ ) a los enteros más cercanos. La segunda diferencia radica en la necesidad de definir cómo un residuo complejo puede ser "menor" que otro Para hacer esto, una función de norma $f (u + vi) = u 2 + v 2$ se define, lo que convierte cada entero gaussiano $u + vi$ en un entero ordinario. Después de cada paso $k$ del algoritmo euclidiano, la norma del resto $f (r k)$ es menor que la norma del resto anterior, $f (r k -1)$ . Dado que la norma es un número entero no negativo y disminuye con cada paso, el algoritmo euclidiano para números enteros gaussianos termina en un número finito de pasos. El resto final distinto de cero es $gcd(α, β)$ , el entero gaussiano de norma más grande que divide tanto $α$ y $β$ ; es único hasta la multiplicación por una unidad, $\pm1$ o $\pm i$ .

Muchas de las otras aplicaciones del algoritmo euclidiano se trasladan a los enteros gaussianos. Por ejemplo, se puede utilizar para resolver ecuaciones diofánticas lineales y problemas de restos chinos para enteros gaussianos; También se pueden definir fracciones continuas de enteros gaussianos.

Dominios euclidianos

Un conjunto de elementos bajo dos operaciones binarias, denotadas como suma y multiplicación, se denomina dominio euclidiano si forma un anillo conmutativo $R$ y, en términos generales, si se puede realizar un algoritmo euclidiano generalizado sobre ellos. Las dos operaciones de tal anillo no necesitan ser la suma y la multiplicación de la aritmética ordinaria; más bien, pueden ser más generales, como las operaciones de un grupo matemático o monoide. No obstante, estas operaciones generales deben respetar muchas de las leyes que rigen la aritmética ordinaria, como la conmutatividad, la asociatividad y la distributividad.

El algoritmo euclidiano generalizado requiere una función euclidiana, es decir, una asignación $f$ de $R$ en el conjunto de enteros no negativos tales que, para dos elementos cualesquiera distintos de cero $a$ y $b$ en $R$ , existen $q$ y $r$ en $R$ tal que $a = qb + r$ y $f (r) < f (b)$ . Ejemplos de dichas asignaciones son el valor absoluto de los enteros, el grado de los polinomios univariados y la norma para los enteros gaussianos anteriores. El principio básico es que cada paso del algoritmo reduce f inexorablemente; por lo tanto, si $f$ se puede reducir solo un número finito de veces, el algoritmo debe detenerse en un número finito de pasos. Este principio se basa en la propiedad de buen orden de los enteros no negativos, que afirma que todo conjunto no vacío de enteros no negativos tiene un miembro más pequeño.

El teorema fundamental de la aritmética se aplica a cualquier dominio euclidiano: cualquier número de un dominio euclidiano se puede factorizar de manera única en elementos irreducibles. Cualquier dominio euclidiano es un dominio de factorización única (UFD), aunque lo contrario no es cierto. Los dominios euclidianos y los UFD's son subclases de los dominios GCD, dominios en los que siempre existe un máximo común divisor de dos números. En otras palabras, puede existir un máximo común divisor (para todos los pares de elementos en un dominio), aunque puede que no sea posible encontrarlo utilizando un algoritmo euclidiano. Un dominio euclidiano es siempre un dominio ideal principal (PID), un dominio integral en el que todo ideal es un ideal principal. Una vez más, lo contrario no es cierto: no todo PID es un dominio euclidiano.

La factorización única de dominios euclidianos es útil en muchas aplicaciones. Por ejemplo, la factorización única de los enteros gaussianos es conveniente para derivar fórmulas para todas las ternas de Pitágoras y para probar el teorema de Fermat en sumas de dos cuadrados. La factorización única también fue un elemento clave en un intento de prueba del último teorema de Fermat publicado en 1847 por Gabriel Lamé, el mismo matemático que analizó la eficiencia del algoritmo de Euclides, basado en una sugerencia de Joseph Liouville. El enfoque de Lamé requería la factorización única de números de la forma $x + ωy$ , donde $x$ y $y$ son números enteros, y ω = e^2iπ/n es una $n$ ésima raíz de 1, es decir, $ω n = 1$ . Aunque este enfoque tiene éxito para algunos valores de $n$ (como $n = 3$ , los números enteros de Eisenstein), en general tales números no se factorizan de forma única. Este fracaso de la factorización única en algunos campos ciclotómicos llevó a Ernst Kummer al concepto de números ideales y, más tarde, a Richard Dedekind a los ideales.

Factorización única de enteros cuadráticos

Distribución de los primos de Eisenstein

u + vω

en el plano complejo, con normas menos de 500. El número

\cdot

es una raíz de cubo de 1.

Los anillos de enteros cuadráticos son útiles para ilustrar los dominios euclidianos. Los enteros cuadráticos son generalizaciones de los enteros gaussianos en los que la unidad imaginaria i se reemplaza por un número $ω$ . Por lo tanto, tienen la forma $u + vω$ , donde $u$ y $v$ son números enteros y $ω$ tiene una de dos formas, dependiendo de un parámetro $D$ . Si $D$ no es igual a un múltiplo de cuatro más uno, entonces

{displaystyle omega ={sqrt {D}}.}

Sin embargo, si D es igual a un múltiplo de cuatro más uno, entonces

{displaystyle omega ={frac {1+{sqrt {D}}}{2}}.}

Si la función $f$ corresponde a una función norma, como la utilizada para ordenar los enteros gaussianos anteriores, entonces el dominio se conoce como norma-euclidiana. Los anillos euclidianos de la norma de los enteros cuadráticos son exactamente aquellos donde $D$ es uno de los valores −11, −7, −3, −2, −1, 2, 3, 5, 6, 7, 11, 13, 17, 19, 21, 29, 33, 37, 41, 57 o 73. Los casos $D = -1$ y $D = -3$ producen los enteros de Gauss y los enteros de Eisenstein, respectivamente.

Si se permite que $f$ sea cualquier función euclidiana, entonces la lista de valores posibles de $D$ cuyo dominio es euclidiano aún no se conoce. El primer ejemplo de un dominio euclidiano que no era euclidiano normativo (con $D = 69$ ) se publicó en 1994. En 1973, Weinberger demostró que un anillo entero cuadrático con $D > 0$ es euclidiano si, y solo si, es un dominio ideal principal, siempre que se cumpla la hipótesis de Riemann generalizada.

Anillos no conmutativos

El algoritmo euclidiano se puede aplicar a algunos anillos no conmutativos, como el conjunto de cuaterniones de Hurwitz. Sean $α$ y $β$ representan dos elementos de tal anillo. Tienen un divisor derecho común $δ$ if $α = ξδ$ y $β = ηδ$ para alguna elección de $ξ$ y $η$ en el anillo. De manera similar, tienen un divisor izquierdo común si $α = dξ$ y $β = dη$ para alguna elección de $ξ$ y $η$ en el anillo. Dado que la multiplicación no es conmutativa, existen dos versiones del algoritmo euclidiano, una para divisores por la derecha y otra para divisores por la izquierda. Al elegir los divisores correctos, el primer paso para encontrar el $mcd(α, β)$ mediante el algoritmo euclidiano se puede escribir

{displaystyle rho _{0}=alpha -psi _{0}beta =(xi -psi _{0}eta)delta}

donde $ψ 0$ representa el cociente y $ρ 0$ el resto. Esta ecuación muestra que cualquier divisor derecho común de $α$ y $β$ es también un divisor común del resto $ρ 0$ . La ecuación análoga para los divisores de la izquierda sería

{displaystyle rho _{0}=alpha -beta psi _{0}=delta (xi -eta psi _{0}).}

Con cualquiera de las opciones, el proceso se repite como se indicó anteriormente hasta que se identifica el máximo común divisor derecho o izquierdo. Como en el dominio euclidiano, el "tamaño" del resto $ρ 0$ (formalmente, su norma) debe ser estrictamente menor que $β$ , y debe haber solo un número finito de tamaños posibles para $ρ 0$ , por lo que se garantiza que el algoritmo terminará.

La mayoría de los resultados del MCD se transfieren a números no conmutativos. Por ejemplo, la identidad de Bézout establece que el derecho $gcd(α, β)$ se puede expresar como un combinación lineal de $α$ y $β. En otras palabras, hay números σ y τ tal que$

{displaystyle Gamma _{text{right}}=sigma alpha +tau beta.}

La identidad análoga para el GCD izquierdo es casi la misma:

{displaystyle Gamma _{text{left}}=alpha sigma +beta tau.}

La identidad de Bézout se puede usar para resolver ecuaciones diofánticas. Por ejemplo, una de las pruebas estándar del teorema de los cuatro cuadrados de Lagrange, que cada número entero positivo puede representarse como una suma de cuatro cuadrados, se basa en los MCD de cuaterniones de esta manera.

Contenido relacionado

Más resultados...