Algoritmo de ley Μ

Companding of μ-law and A-law algoritmos

Comparación de calidad de audio

μ-law conversion

---

Original file

---

¿Problemas para reproducir estos archivos? Vea la ayuda de los medios.

El algoritmo de ley μ (a veces escrito ley-mu, a menudo aproximado como ley-u) es un algoritmo de compresión, utilizado principalmente en sistemas de telecomunicaciones digitales PCM de 8 bits en América del Norte y Japón. Es una de las dos versiones del estándar G.711 de ITU-T, siendo la otra versión la ley A similar. La ley A se utiliza en regiones donde las señales de telecomunicaciones digitales se transportan en circuitos E-1, p. Europa.

Los algoritmos de compansión reducen el rango dinámico de una señal de audio. En los sistemas analógicos, esto puede aumentar la relación señal-ruido (SNR) lograda durante la transmisión; en el dominio digital, puede reducir el error de cuantificación (por lo tanto, aumentar la relación señal-ruido de cuantificación). Estos aumentos de SNR se pueden cambiar por ancho de banda reducido para SNR equivalente.

Tipos de algoritmo

El algoritmo de ley μ se puede describir en forma analógica y en forma digital cuantificada.

Continuo

función μ-law

Función inversa μ-law

Para una entrada determinada x, la ecuación para la codificación de la ley μ es

F()x)=Sgn⁡ ⁡ ()x)In⁡ ⁡ ()1+μ μ SilencioxSilencio)In⁡ ⁡ ()1+μ μ ),− − 1≤ ≤ x≤ ≤ 1,{displaystyle F(x)=operatorname {sgn}(x){dfrac {ln(1+mu ANTERIJO ANTERIVADA)}{ln(1+mu)}},quad -1leq xleq 1,}

donde μ = 255 en los estándares norteamericano y japonés, y sgn(x) es la función de signo. Es importante notar que el rango de esta función es −1 a 1.

La expansión de la ley µ viene dada por la ecuación inversa:

F− − 1()Sí.)=Sgn⁡ ⁡ ()Sí.)()1+μ μ )SilencioSí.Silencio− − 1μ μ ,− − 1≤ ≤ Sí.≤ ≤ 1.{displaystyle F^{-1}(y)=operatorname {sgn}(y){dfrac {(1+mu)}{mu }}quad -1leq yleq 1.}

Discreta

La forma discreta se define en la Recomendación ITU-T G.711.

G.711 no está claro acerca de cómo codificar los valores en el límite de un rango (por ejemplo, si +31 codifica a 0xEF o 0xF0). Sin embargo, G.191 proporciona un código de ejemplo en lenguaje C para un codificador de ley μ. La diferencia entre los rangos positivo y negativo, p. el rango negativo correspondiente a +30 a +1 es −31 a −2. Esto se explica por el uso del complemento a 1 (inversión simple de bits) en lugar del complemento a 2 para convertir un valor negativo en un valor positivo durante la codificación.

Implementación

El algoritmo de la ley μ se puede implementar de varias maneras:

Analog

Utilice un amplificador con ganancia no lineal para lograr la compandación enteramente en el dominio analógico.

Non-linear ADC

Utilice un convertidor analógico a digital con niveles de cuantificación que son desigualmente espaciados para que coincida con el algoritmo μ-law.

Digital

Utilice la versión digital cuantificada del algoritmo μ-law para convertir datos una vez que esté en el dominio digital.

Software/DSP

Utilice la versión continua del algoritmo μ-law para calcular los valores compandados.

Justificación de uso

Se utiliza la codificación de ley μ porque el habla tiene un amplio rango dinámico. En la transmisión de señales analógicas, en presencia de un ruido de fondo relativamente constante, se pierden los detalles más finos. Dado que la precisión de los detalles se ve comprometida de todos modos, y suponiendo que la señal sea percibida como audio por un ser humano, se puede aprovechar el hecho de que el nivel de intensidad acústica percibido o el volumen son logarítmicos al comprimir la señal usando un logarítmico. -amplificador operacional de respuesta (ley de Weber-Fechner). En los circuitos de telecomunicaciones, la mayor parte del ruido se inyecta en las líneas, por lo tanto, después del compresor, la señal deseada se percibe significativamente más alta que la estática, en comparación con una fuente sin comprimir. Esto se convirtió en una solución común y, por lo tanto, antes del uso digital común, se desarrolló la especificación de la ley μ para definir un estándar interoperable.

En los sistemas digitales, este algoritmo preexistente tuvo el efecto de reducir significativamente la cantidad de bits necesarios para codificar la voz humana reconocible. Usando la ley μ, una muestra podría codificarse efectivamente en tan solo 8 bits, un tamaño de muestra que coincidía convenientemente con el tamaño de símbolo de la mayoría de las computadoras estándar.

La codificación de la ley μ redujo efectivamente el rango dinámico de la señal, lo que aumentó la eficiencia de la codificación mientras polariza la señal de una manera que da como resultado una relación señal-distorsión que es mayor que la obtenida por la codificación lineal para un determinado número de bits

μ-law decodificación como generado con el Sun Microsystems C-language rutina g711.c comúnmente disponible en Internet.

El algoritmo de ley μ también se usa en el formato.au, que se remonta al menos a SPARCstation 1 de Sun Microsystems como el método nativo usado por la interfaz /dev/audio, ampliamente utilizado como estándar de facto para sonido en sistemas Unix. El formato au también se usa en varias API de audio comunes, como las clases en el paquete Java sun.audio en Java 1.1 y en algunos métodos de C#.

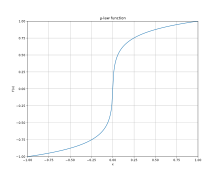
Este gráfico ilustra cómo la ley μ concentra el muestreo en los valores más pequeños (más suaves). El eje horizontal representa los valores de byte 0-255 y el eje vertical es el valor decodificado lineal de 16 bits de la codificación de ley μ.

Comparación con la ley A

El algoritmo de ley μ proporciona un rango dinámico ligeramente mayor que el de ley A a costa de peores distorsiones proporcionales para señales pequeñas. Por convención, la ley A se usa para una conexión internacional si al menos un país la usa.