Icosaedro regular

icosahedron regular
(Clique aqui para girar modelo)
Tipo	sólido platônico
Elementos	F 20, E = 30 V = 12 (χ = 2)
Faces por lados	20.
Notação de saída	Eu... S T
Símbolos de Schläfli	(3,5)
	- Sim. sr. S(33?{displaystyle s{begin{Bmatrix}33end{Bmatrix}}}
Configuração da face	V5.5.5.
Símbolo de Wythoff	5 | 2 3
Diagrama de Coxeador
Simetria	Ih, H3[5,3], (*532)
Grupo de rotação	Eu...+, (532)
Referências	U22C25,4
Propriedades	regular, convexdeltahedron
Ângulo dihedral	138.189685° = arcos(−√5?3)
3.3.3 (Vertex figure)	Dodecaedron regular (poliédron dual)
Rede

Modelo 3D de um icosahedron regular

Em geometria, um icosaedro regular (ou) é um poliedro convexo com 20 faces, 30 arestas e 12 vértices. É um dos cinco sólidos platônicos e aquele com mais faces.

Tem cinco faces triangulares equiláteras que se encontram em cada vértice. É representado por seu símbolo Schläfli {3,5}, ou às vezes por sua figura de vértice como 3.3.3.3.3 ou 3⁵. É o dual do dodecaedro regular, que é representado por {5,3}, possuindo três faces pentagonais ao redor de cada vértice. Na maioria dos contextos, o uso não qualificado da palavra "icosaedro" refere-se especificamente a esta figura.

Um icosaedro regular é um deltaedro estritamente convexo e uma bipirâmide pentagonal giro-alongada e um antiprisma pentagonal bi-aumentado em qualquer uma das seis orientações.

O nome vem do grego εἴκοσι (eíkosi) 'vinte' e ἕδρα (hédra) 'assento'. O plural pode ser "icosaedros" ou "icosaedra" ().

Dimensões

Rede dobrável em icosahedron

Se o comprimento da borda de um icosahedron regular é umNão., o raio de uma esfera circunscrita (que toca o icosaedro em todos os vértices) é

Ru= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um2φ φ 5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um410.+25= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umpecado⁡ ⁡ 2D D 5? ? 0,95105651)) umNão. ? Não. {5}}}={frac {a}{4}}{sqrt {10+2{sqrt {5}}=asin {frac {2pi} }{5}}} 0.951,056,5163cdot a}

REu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ 2um23= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =312(3+5)um? ? 0,757613141)) umNão. r_{i}={frac (varphi ^{2}a}{2{sqrt {3}}={frac {sqrt {3}}{12}}left(3+{sqrt {5}}right)aapprox 0.755,761,3141cdot a}

Rm= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umφ φ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =14(1+5)um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ume⁡ ⁡ D D 5? ? 0.80901699)) umNão. r_{m}={frac (avarphi }{2}}={frac {1}{4}}left(1+{sqrt {5}}right)a=acos {frac {pi }{5}}} 0.809,016,99cdot a}

φ φ - Sim.

Área e volume

A área de superfície ANão. A. e o volume VNão. de um icosahedron regular de comprimento da borda umNão. são:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =53um2? ? 8.66025404um2{displaystyle A=5{sqrt {3}}a^{2}approx 8.660,254,04a^{2}}

V= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =512(3+5)um3? ? 2.181.69499um3{displaystyle V={frac {5}{12}}left(3+{sqrt {5}}right)a^{3}approx 2.181,694,99a^{3}}

34um2- Sim. {3}}{4}}a^{2}}

REu...Não. r_{i}}

O fator de preenchimento de volume da esfera circunscrita é:

f= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =V43D D Ru3= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =20.(3+5)(25+10.)32D D ? ? 0.6054613829,Não. Não. {4}{3}pi r_{u}^{3}}}={frac {20left(3+{sqrt {5}}right)}{left(2{sqrt {5}}+10right)^{frac {3}{2}}pi }}approx 0.605,461,3829,}

A esfera média de um icosaedro terá um volume 1,01664 vezes o volume do icosaedro, que é de longe a semelhança mais próxima em volume de qualquer sólido platônico com sua esfera média. Isso sem dúvida torna o icosaedro o "mais redondo" dos sólidos platônicos.

Coordenadas cartesianas

Os vértices de Icosahedron formam três retângulos de ouro ortogonais

Os vértices de um icosahedron centralizados na origem com um comprimento de borda de 2 e um circunradius de φ φ 2+1? ? 1.902{textstyle {sqrt {varphi ^{2}+1}}approx 1.902} são

(0,± ± 1,± ± φ φ ){displaystyle (0,pm 1,pm varphi)}

(± ± 1,± ± φ φ ,0)(pm 1,pm varphi0)}

(± ± φ φ ,0,± ± 1)(pm varphi0,pm 1)}

φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1+52- Sim. - Sim. (em inglês) {5}}}{2}}}

Os vértices do icosaedro formam cinco conjuntos de três retângulos áureos concêntricos, mutuamente ortogonais, cujas arestas formam anéis borromeanos.

Se o icosahedron original tem comprimento de borda 1, seu dodecahedron duplo tem comprimento de borda 1φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ - Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5- Sim. - Sim. 12- Não. }}=varphi -1={frac Não. {5}}-1}{2}}}.

Modelo de um icosahedron feito com esferas metálicas e conectores magnéticos

As 12 arestas de um octaedro regular podem ser subdivididas na proporção áurea para que os vértices resultantes definam um icosaedro regular. Isso é feito primeiro colocando vetores ao longo das arestas do octaedro de modo que cada face seja delimitada por um ciclo e, em seguida, subdividindo de forma semelhante cada aresta na média áurea ao longo da direção de seu vetor. Os cinco octaedros que definem qualquer icosaedro formam um composto poliédrico regular, enquanto os dois icosaedros que podem ser definidos dessa maneira a partir de qualquer octaedro formam um composto poliedro uniforme.

icosaedro regular e sua esfera circunscrita. Os vértices do icosaedro regular encontram-se em quatro planos paralelos, formando neles quatro triângulos equiláteros; isto foi provado pelo Pappus de Alexandria

Os vértices de um icosahedron centralizados na origem com um comprimento de borda 2)) (1- Sim. - Sim. 15)? ? 1.051(2cdot left(1-{frac {1}{sqrt {5}}}right)}}approx 1.051} e um circunrádio de 1 (com quatro pontos deitado no plano x-y) são

± ± (1,0,0){displaystyle pm (1,0,0)}

± ± (15,25,0){displaystyle pm left({frac {1}{sqrt {5}}},{frac {2}{sqrt {5}}},0right)}

± ± (15,1- Sim. - Sim. 152,± ± 1+152){displaystyle pm left({frac {1}{sqrt {5}}},{frac {1-{frac Não. {5}}{2}},pm {sqrt {frac (1+{frac) {5}}{2}}}right)}

± ± (15,- Sim. - Sim. 1- Sim. - Sim. 152,± ± 1- Sim. - Sim. 152){displaystyle pm left({frac {1}{sqrt {5}}},{frac {-1-{frac Não. {5}}{2}},pm {sqrt {frac {1-{frac Não. {5}}{2}}}right)}

Coordenadas esféricas

As localizações dos vértices de um icosaedro regular podem ser descritas usando coordenadas esféricas, por exemplo, como latitude e longitude. Se dois vértices são considerados nos pólos norte e sul (latitude ±90°), então os outros dez vértices estão na latitude ± arctan 1/2 = ±26,57°. Esses dez vértices estão em longitudes uniformemente espaçadas (36° de distância), alternando entre as latitudes norte e sul.

Este esquema aproveita o fato de que o icosaedro regular é uma bipirâmide giro-alongada pentagonal, com simetria diédrica D_5d, ou seja, é formado por duas pirâmides pentagonais congruentes unidas por um antiprisma pentagonal.

Projeções ortogonais

O icosaedro tem três projeções ortogonais especiais, centradas em uma face, uma aresta e um vértice:

Projeções ortogonais

Centro por	Cara	Borda	Verbos
Avião de Coxeador	A2	A3	H. H. H.3
Gráfico
Projeto simetria	[6]	[2]	[10]
Gráfico	Cara normal	Borda normal	Vertex normal

Como configuração

Esta matriz de configuração representa o icosaedro. As linhas e colunas correspondem a vértices, arestas e faces. Os números diagonais dizem quantos de cada elemento ocorrem em todo o icosaedro. Os números não diagonais dizem quantos elementos da coluna ocorrem dentro ou no elemento da linha.

Não.125523023320.]{displaystyle {begin{bmatrix}{begin{matrix}12&5&52&30&23&3&20end{matrix}}end{bmatrix}}}

Aqui está a configuração expandida com elementos k-face e figuras k. As contagens de elementos diagonais são a proporção do grupo Coxeter completo H₃, ordem 120, dividida pela ordem do subgrupo com remoção de espelho.

H. H. H.3		k-face	fk	f0	f1	f2	k-fig	Notas
A2		()	f0	12	5	5	(5)	H. H. H.3/H2 = 120/10 = 12
A1A1		Não.	f1	2	30	2	Não.	H. H. H.3/A1A1 = 120/4 = 30
H. H. H.2		Não.	f2	3	3	20.	()	H. H. H.3/A2 = 120/6 = 20

Telha esférica

O icosaedro também pode ser representado como um ladrilho esférico e projetado no plano por meio de uma projeção estereográfica. Essa projeção é conforme, preservando ângulos, mas não áreas ou comprimentos. Linhas retas na esfera são projetadas como arcos circulares no plano.

Projeção ortográfico	Projeção estereográfica

Outros fatos

• Um icosahedron tem 43.380 redes distintas.
• Para colorir o icosahedron, tal que nenhum dois rostos adjacentes têm a mesma cor, requer pelo menos 3 cores.
• Um problema que remonta aos gregos antigos é determinar qual de duas formas tem volume maior, um icosaedro inscrito em uma esfera, ou um dodecaedro inscrito na mesma esfera. O problema foi resolvido por Hero, Pappus e Fibonacci, entre outros. Apollonius de Perga descobriu o resultado curioso de que a proporção de volumes dessas duas formas é a mesma que a relação de suas áreas de superfície. Ambos os volumes têm fórmulas envolvendo a proporção de ouro, mas tomadas para diferentes poderes. Como resulta, o icosaedro ocupa menos do volume da esfera (60.54%) do que o dodecaedro (66,49%).
• Ângulo cosahedral - o ângulo entre os vértices mais próximos do icosahedron, em relação ao centro do corpo do icosahedron (3D), é igual ao ângulo diagonal de um quadrado duplo e / ou meio (≈ 63.434949°)

Construção por um sistema de linhas equiangulares

Icosahedron H. H. H.3 Avião de Coxeador	6-ortoplex D6 Avião de Coxeador
Esta construção pode ser geometricamente vista como os 12 vértices do 6-ortoplex projetado para 3 dimensões. Isto representa uma dobra geométrica do D6 para H3 Grupos de coxer: Visto por estas projeções ortogonais do plano 2D Coxeter, os dois vértices centrais sobrepostos definem o terceiro eixo neste mapeamento.

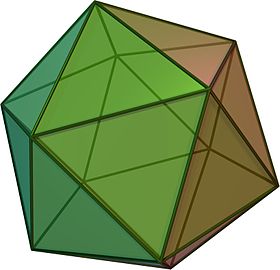
A seguinte construção do icosahedron evita computação tediosa no campo número QNão.5]{displaystyle mathbb {Q} [{sqrt {5}}} necessário em abordagens mais elementares.

A existência do icosaedro equivale à existência de seis linhas equiangulares em R3{displaystyle mathbb {R} ^{3}}. De fato, intersectando tal sistema de linhas equiangulares com uma esfera euclidiana centrada em sua interseção comum produz os doze vértices de um icosaedro regular como pode facilmente ser verificado. Por outro lado, supondo a existência de um icosaedro regular, as linhas definidas por seus seis pares de vértices opostos formam um sistema equiangular.

Para construir tal sistema equiangular, começamos com esta matriz quadrada 6 × 6:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(011111101- Sim. - Sim. 1- Sim. - Sim. 111101- Sim. - Sim. 1- Sim. - Sim. 11- Sim. - Sim. 1101- Sim. - Sim. 11- Sim. - Sim. 1- Sim. - Sim. 110111- Sim. - Sim. 1- Sim. - Sim. 110).A=left({begin{array}{crrr}0&1&1&1&1&1&1\1&1&1&-1&1\1&1&0&1&1&1&1&1&1&1&1&1-1&1-1-1-1&1-1&1-1&1-1&1-0-end. ?

Um rendimento de computação simples A2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5Eu...Não. A^{2}=5I} (onde) Eu...Não. Eu... é a matriz de identidade 6 × 6). Isso implica que ANão. A. tem eigenvalues - Sim. - Sim. 5(5}}} e 5(5}}}, ambos com multiplicidade 3 desde ANão. A. é simétrico e de traço zero.

A matriz A+5Eu...{displaystyle A+{sqrt {5}}I} induz assim uma estrutura euclidiana no espaço quociente R6/ker⁡ ⁡ (A+5Eu...){displaystyle mathbb {R} ^{6}/operatorname {ker} (A+{sqrt {5}}I)}, que é isomorfo R3{displaystyle mathbb {R} ^{3}} desde o kernel ker⁡ ⁡ (A+5Eu...)(A+{sqrt {5}}I)} de A+5Eu...{displaystyle A+{sqrt {5}}I} dimensão 3. A imagem sob a projeção D D :R6→ → R6/ker⁡ ⁡ (A+5Eu...){displaystyle pi:mathbb {R} ^{6}to mathbb {R} ^{6}/operatorname {ker} (A+{sqrt {5}}I)} dos seis eixos de coordenadas R6{displaystyle mathbb {R} ^{6}} forma um sistema de seis linhas equiangulares em R3{displaystyle mathbb {R} ^{3}} intersecção em pares em um ângulo agudo comum Arcos⁡ ⁡ 1/5{displaystyle arccos 1/{sqrt (5). Projeção ortogonal dos vetores de base positiva e negativa de R6{displaystyle mathbb {R} ^{6}} sobre a 5(5}}}- espaço de ANão. A. produz assim os doze vértices do icosahedron.

Uma segunda construção direta do icosahedron usa a teoria da representação do grupo alternado A5Não. A_{5}} agindo por isometrias diretas no icosahedron.

Simetria

A simetria Icosahedral completa tem 15 planos de espelho (visto como cyan grandes círculos nesta esfera) reunião em ordem D D /5,D D /3,D D /2{displaystyle pi /5,pi /3,pi /2} ângulos, dividindo uma esfera em 120 domínios fundamentais triângulo. Existem 6 eixos 5 vezes (azul), 10 eixos 3 vezes (vermelho), e 15 eixos 2 vezes (magenta). Os vértices do icosahedron regular existem nos pontos do eixo de rotação de 5 vezes.

O grupo de simetria rotacional do icosaedro regular é isomorfo ao grupo alternado de cinco letras. Este grupo simples não abeliano é o único subgrupo normal não trivial do grupo simétrico em cinco letras. Como o grupo de Galois da equação quíntica geral é isomórfico ao grupo simétrico de cinco letras, e esse subgrupo normal é simples e não abeliano, a equação quíntica geral não tem solução em radicais. A prova do teorema de Abel-Ruffini usa esse fato simples, e Felix Klein escreveu um livro que fez uso da teoria das simetrias icosaédricas para derivar uma solução analítica para a equação quíntica geral (Klein 1884). Veja simetria icosaédrica: geometrias relacionadas para mais história e simetrias relacionadas em sete e onze letras.

O grupo de simetria completa do icosahedron (incluindo reflexões) é conhecido como o grupo icosahedral completo, e é isomorphic ao produto do grupo de simetria rotacional e do grupo C2{displaystyle C_{2}} do tamanho dois, que é gerado pela reflexão através do centro do icosahedron.

Estelações

O icosaedro tem um grande número de estrelas. De acordo com regras específicas definidas no livro Os Cinquenta e Nove Icosaedros, foram identificadas 59 estrelas para o icosaedro regular. A primeira forma é o próprio icosaedro. Um deles é um poliedro regular de Kepler-Poinsot. Três são poliedros compostos regulares.

21 de 59 estelações

Os rostos do icosahedron estenderam-se para fora como os planos se cruzam, definindo regiões no espaço como mostrado por este diagrama de estelação das interseções em um único plano.

Faceting

O pequeno dodecaedro estrelado, o grande dodecaedro e o grande icosaedro são três facetas do icosaedro regular. Eles compartilham o mesmo arranjo de vértices. Todos eles têm 30 arestas. O icosaedro regular e o grande dodecaedro compartilham o mesmo arranjo de arestas, mas diferem nas faces (triângulos versus pentágonos), assim como o pequeno dodecaedro estrelado e o grande icosaedro (pentagramas versus triângulos).

Convexo	Estrelas regulares
- Não.	grande dodecaedron	pequeno dodecaedro estelarizado	grande icosahedron

Relações geométricas

Inscrito em outros sólidos platônicos

O icosaedro regular é o poliedro dual do dodecaedro regular. Um icosaedro pode ser inscrito em um dodecaedro colocando seus vértices nos centros das faces do dodecaedro e vice-versa.

Um icosaedro pode ser inscrito em um octaedro colocando seus 12 vértices nas 12 arestas do octaedro de forma que eles dividam cada aresta em suas duas seções áureas. Como as seções áureas são desiguais, existem cinco maneiras diferentes de fazer isso consistentemente, então cinco icosaedros disjuntos podem ser inscritos em cada octaedro.

Um icosahedron de comprimento da borda 1φ φ ? ? 0.618{textstyle {frac {1}{varphi }}approx 0.618} pode ser inscrito em um cubo de comprimento unitário colocando seis de suas bordas (3 pares opostas ortogonais) nas faces quadradas do cubo, centrado nos centros de face e paralelo ou perpendicular às bordas do quadrado. Porque há cinco vezes mais bordas icosahedron como rostos cubo, há cinco maneiras de fazer isso consistentemente, então cinco icosahedra disjoint pode ser inscrito em cada cubo. Os comprimentos de borda do cubo e o icosahedron inscrito estão na proporção de ouro.

Relações com as 600 células e outros 4 politopos

O icosaedro é o análogo dimensional da célula 600, um politopo regular de 4 dimensões. A célula 600 tem seções transversais icosaédricas de dois tamanhos, e cada um de seus 120 vértices é uma pirâmide icosaédrica; o icosaedro é a figura do vértice da célula 600.

A unidade-radius 600-célula tem células tetraedrais do comprimento da borda 1φ φ ? ? 0.618{textstyle {frac {1}{varphi }}approx 0.618}, 20 dos quais se encontram em cada vértice para formar uma pirâmide icosaedral (uma 4-piramida com um icosaedro como sua base). Assim, a 600-célula contém 120 icosahedra de comprimento da borda 1φ φ ? ? 0.618{textstyle {frac {1}{varphi }}approx 0.618}. O 600-célula também contém cubos de comprimento unitário e octahedra de comprimento unitário como características interiores formadas por seus acordes de comprimento unitário. Na unidade-rádio 120-célula (outro 4-polytope regular que é tanto o dual da 600-célula e um composto de 5 600-células) encontramos todos os três tipos de icosahedra inscrito (em um dodecaedro, em um octahedron, e em um cubo).

Um 4-politopo semirregular, o snub 24-cell, possui células icosaédricas.

Relações com outros politopos uniformes

O icosaedro é único entre os sólidos platônicos por possuir um ângulo diedro não inferior a 120°. Seu ângulo diedro é de aproximadamente 138,19°. Assim, assim como os hexágonos têm ângulos não inferiores a 120° e não podem ser usados como as faces de um poliedro regular convexo porque tal construção não atenderia ao requisito de que pelo menos três faces se encontrassem em um vértice e deixassem um defeito positivo para dobrar em três dimensões, os icosaedros não podem ser usados como as células de um policórnio regular convexo porque, da mesma forma, pelo menos três células devem se encontrar em uma borda e deixar um defeito positivo para dobrar em quatro dimensões (em geral para um politopo convexo em n dimensões, pelo menos três facetas devem se encontrar em um pico e deixar um defeito positivo para dobrar em n-espaço). No entanto, quando combinados com células adequadas com ângulos diedros menores, os icosaedros podem ser usados como células em policoros semi-regulares (por exemplo, o snub 24-cell), assim como os hexágonos podem ser usados como faces em poliedros semi-regulares (por exemplo, o icosaedro truncado). Finalmente, os politopos não convexos não possuem os mesmos requisitos estritos dos politopos convexos, e os icosaedros são de fato as células do icosaédrico de 120 células, um dos dez policoros regulares não convexos.

Existem distorções do icosaedro que, embora não sejam mais regulares, são uniformes nos vértices. Estes são invariantes sob as mesmas rotações que o tetraedro, e são um pouco análogos ao cubo arrebitado e ao dodecaedro arrebitado, incluindo algumas formas que são quirais e algumas com T_h-simetria, ou seja, têm diferentes planos de simetria do tetraedro.

Um icosaedro também pode ser chamado de bipirâmide pentagonal giro-alongada. Pode ser decomposto em uma pirâmide pentagonal giro-alongada e uma pirâmide pentagonal ou em um antiprisma pentagonal e duas pirâmides pentagonais iguais.

Relação com o triacontaedro de 6 cubos e rômbico

O icosahedron pode ser projetado para 3D do 6D 6-demicube usando os mesmos vetores de base que formam o casco do triacontaedro Rhombic do 6-cubo. Mostrado aqui, incluindo os 20 vértices internos que não estão conectados pelas 30 bordas exteriores do casco do comprimento da norma 6D 2(2}}}. Os vértices internos formam um dodecaedro.

Os vetores de base de projeção 3D [u,v,w] usados são:

u= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(1,φ φ ,0,- Sim. - Sim. 1,φ φ ,0)v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(φ φ ,0,1,φ φ ,0,- Sim. - Sim. 1)O quê?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(0,1,φ φ ,0,- Sim. - Sim. 1,φ φ ){displaystyle {begin{aligned}u&=(1,varphi0,-1,varphi0)v&=(varphi0,1,varphi0,-1)w&=(0,1,varphi0,-1,varphi)\end{aligned}}}

Simetrias

Subgrupos de simetria cosahedral

Existem 3 cores uniformes do icosaedro. Essas cores podem ser representadas como 11213, 11212, 11111, nomeando as 5 faces triangulares ao redor de cada vértice por sua cor.

O icosaedro pode ser considerado um tetraedro arrebitado, pois a esnobificação de um tetraedro regular resulta em um icosaedro regular com simetria tetraédrica quiral. Também pode ser construído como um octaedro truncado alternado, com simetria piritoédrica. A versão de simetria piritoédrica às vezes é chamada de pseudoicosaedro e é dual ao piritoedro.

	Regular	Uniforme		2-uniformidade			3-uniformidade
Nome	Regular - Não.	Snuboctahedron	Linha de produção	Gyrolongedpentagonalbipiramid	Anúncio grátis para sua empresa	Snub triangular antiprisma	Praça Snub Bipiramida
Imagem
Facecoloração	(111)	(1121)	(1121)	(11122) (22222)	(1233) (23333)	(1121) (1121)	(11424) (22434) (33414)
Medidores de água
Produtos de plástico	(3,5)	- Sim.	Sr.	() | {n} | r{n} | ())		- Sim.	Sdt{2,4}
Conway	Eu...	HtO	S T	k5A5		SY3 = HtA3	HtdP4
Simetria	Eu...h [5,3] (*532)	Th [3]+,4] (3*2)	T [3,3]+ (332)	D5d [2]+10. (2*5)	D3D [2]+, (2*3)	D3 [3,2]+ (32)	D2h [2,2] (*222)
Simetria ordem	120	24.	12	20.	12	6	8

Usos e formas naturais

nanopartícula de ouro vista por microscopia eletrônica de transmissão.

Estrutura de γ-boron.

Biologia

Muitos vírus, por ex. vírus do herpes, têm conchas icosaédricas. As estruturas virais são construídas de subunidades de proteínas idênticas repetidas conhecidas como capsômeros, e o icosaedro é a forma mais fácil de montar usando essas subunidades. Um poliedro regular é usado porque pode ser construído a partir de uma única unidade básica de proteína usada repetidas vezes; isso economiza espaço no genoma viral.

Várias organelas bacterianas com formato icosaédrico também foram encontradas. As enzimas que encapsulam o invólucro icosaédrico e os intermediários lábeis são constituídos por diferentes tipos de proteínas com domínios BMC.

Em 1904, Ernst Haeckel descreveu várias espécies de Radiolaria, incluindo Circogonia icosahedra, cujo esqueleto tem a forma de um icosaedro regular. Uma cópia da ilustração de Haeckel para este radiolário aparece no artigo sobre poliedros regulares.

Química

Os closo-carboranos são compostos químicos com forma muito próxima do icosaedro. A geminação icosaédrica também ocorre em cristais, especialmente nanopartículas.

Muitos boretos e alótropos de boro contêm boro B₁₂ icosaedro como unidade estrutural básica.

Brinquedos e jogos

Morrer de vinte lados do Egito Ptolemaico

Morrer de vinte lados

Dados icosaédricos com vinte lados têm sido usados desde os tempos antigos.

Em vários jogos de RPG, como Dungeons & Dragões, o dado de vinte lados (d20 para abreviar) é comumente usado para determinar o sucesso ou falha de uma ação. Este dado tem a forma de um icosaedro regular. Pode ser numerado de "0" para "9" duas vezes (na forma em que geralmente serve como um dado de dez lados, ou d10), mas a maioria das versões modernas são rotuladas de "1" para "20".

Um icosaedro é usado no jogo de tabuleiro Scattergories para escolher uma letra do alfabeto. Seis letras são omitidas (Q, U, V, X, Y e Z).

No jogo Nintendo 64 Kirby 64: The Crystal Shards, o chefe Miracle Matter é um icosaedro normal.

Dentro de uma Magic 8-Ball, várias respostas para perguntas sim-não estão inscritas em um icosaedro regular.

Tensegrity

O octaedro tem sido amplamente estudado no campo da tensegridade. Devido à sua simetria esférica e alta resistência à relação de massa, a forma tornou-se um bom candidato para estruturas espaciais implantáveis de tensegridade, como o SuperBALL da NASA. O robô é composto por hastes, cabos e atuadores de diferentes escalas e está atualmente em desenvolvimento entre o Grupo de Robótica Inteligente do Centro de Pesquisa Ames da NASA e o Laboratório de Robótica de Tensegridade Dinâmica (DTRL). Sua configuração não implantada é altamente compacta, portanto, ideal para caber dentro das restrições de espaço das carenagens de foguetes.

O Icosaedro em tensegridade é composto por seis suportes e vinte e quatro cabos que conectam doze nós. Um estado de autoestresse está presente dentro da combinação alcançada através do uso da morfogênese celular.

Outros

R. Buckminster Fuller e o cartógrafo japonês Shoji Sadao desenharam um mapa-múndi na forma de um icosaedro desdobrado, chamado de projeção Fuller, cuja distorção máxima é de apenas 2%.

A dupla americana de música eletrônica ODESZA usa um icosaedro regular como logotipo.

Gráfico icosaédrico

O esqueleto do icosaedro (os vértices e arestas) forma um gráfico. É um dos 5 grafos platônicos, cada um um esqueleto de seu sólido platônico.

O alto grau de simetria do polígono é replicado nas propriedades deste gráfico, que é transitivo à distância e simétrico. O grupo de automorfismo tem ordem 120. Os vértices podem ser coloridos com 4 cores, as arestas com 5 cores e o diâmetro é 3.

O grafo icosaédrico é hamiltoniano: existe um ciclo contendo todos os vértices. Também é um grafo planar.

Projeção ortogonal

Icosaedro regular diminuído

Existem 4 sólidos de Johnson relacionados, incluindo faces pentagonais com um subconjunto de 12 vértices. O icosaedro regular dissecado semelhante tem 2 vértices adjacentes diminuídos, deixando duas faces trapezoidais, e um bifastígio tem 2 conjuntos opostos de vértices removidos e 4 faces trapezoidais. O antiprisma pentagonal é formado pela remoção de dois vértices opostos.

Formulário	J2	Bicárnio	J63	J62	Linha de produção	S{2,10}	J11
Versículos	6 de 12	8 de 12	9 de 12	10 de 12			11 de 12
Simetria	C5[5], (*55) ordem 10	D2h, [2,2], *222 ordem 8	C3, [3], (*33) ordem 6	C2[2], (*22) ordem 4		D5d, [2+,10], (2*5) ordem 20	C5[5], (*55) ordem 10
Imagem

Poliedros e politopos relacionados

O icosaedro pode ser transformado por uma sequência de truncamento em seu dual, o dodecaedro:

Família de polihedra icosaedral uniforme
Simetria: [5,3], (*532)							[5,3]+, (532)
{5,3}	Não.	?	T3,5	(3,5)	rr{5,3}	Não.	Sr.
Duals para polihedra uniforme
V5.5.5.	V3.10.10	V3.5.	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Como um tetraedro achatado e alternância de um octaedro truncado, também existe nas famílias de simetria tetraédrica e octaédrica:

Família de polihedra tetraedral uniforme
Simetria: [3,3], (*332)							[3,3]+, (332)
(3,3)	T3,3	R3,3	T3,3	(3,3)	rr{3,3]	3,3	Sr.
Duals para polihedra uniforme
V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Poliedros octahedral uniforme
Simetria: [4,3], (*432)							[4,3]+ (432)	[2]+[3,3] (*332)		[3]+,4] (3*2)
{4,3}	Não.	R{4,3} RECURSOS1.1?	T3,4 )1.1?	{3,4} (1.1?	rr,3 S2{3,4}	Não.	Sr.	H{4,3} (3,3)	H2{4,3} T3,3	- Sim. )1.1?
		= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =				= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ou	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ou	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
Duals para polihedra uniforme
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V3	V3.62	V35

Este poliedro está topologicamente relacionado como parte da sequência de poliedros regulares com símbolos Schläfli {3,n}, continuando no plano hiperbólico.

*n32 mutação simetria de camadas regulares: {3,n? v ) e
Esférica				Euclid.	Hip compacto.		Paraco.	Hiperbólico não-compacto
3.3	33	34	35	36	37	38	3 ∞	312	39	36	33

O icosahedron regular, visto como um O que se passa?, é um membro de uma seqüência de poliedros e tilings com figura de vértice (3.3.3.3.n) e diagrama de Coxeter-Dynkin . Estes números e suas duplas têm (n32) simetria rotacional, estando no plano euclidiano para n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =6Não., e plano hiperbólico para qualquer mais alto nNão.. A série pode ser considerada para começar n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2Não., com um conjunto de rostos degenerados em digons.

n32 mutações de simetria de teias snub: 3.3.3.3.n v ) e
Simetria n.o 32	Esférica				Euclidiano	Hiperbólica compacta		Paracomp.
	232	332	432	532	632	732	832	∞32
Snub números
Config.	3.3.3.3.2	3.3.3	3.3.3.3.4	3.3.3.3	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Gyro números
Config.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Esférica		Tilings hiperbólicos v ) e
(2,5)	(3,5)	(4,5)	(5,5)	Não.	(7,5)	(8,5)	...	(∞,5)

O icosaedro pode pavimentar o espaço hiperbólico no favo de mel icosaédrico da ordem 3, com 3 icosaedros ao redor de cada borda, 12 icosaedros ao redor de cada vértice, com o símbolo Schläfli {3,5,3}. É um dos quatro mosaicos regulares no 3-espaço hiperbólico.

É mostrado aqui como uma estrutura de borda em um modelo de disco Poincaré, com um icosahedron visível no centro.