Statistique inférentielle

ImprimirCitar

L'inférence statistique ou les statistiques inférentielles est le processus d'utilisation de l'analyse de données pour déduire les propriétés d'une distribution de probabilité sous-jacente. L'analyse statistique inférentielle déduit les propriétés d'une population, par exemple, en testant des hypothèses et en dérivant des estimations. L'ensemble de données observé est supposé être tiré d'une population plus large.

Les statistiques inférentielles peuvent être comparées aux statistiques descriptives. Les statistiques descriptives ne traitent que des propriétés des données observées et ne reposent pas sur l'hypothèse que les données proviennent d'une population plus large. Dans l'apprentissage automatique, le terme inférence est parfois utilisé à la place pour signifier "faire une prédiction, évaluer un modèle déjà formé"; dans ce contexte, l'inférence des propriétés du modèle est appelée formation ou apprentissage (plutôt que inférence), et l'utilisation d'un modèle pour la prédiction est appelée inférence (plutôt que prédiction); voir aussi inférence prédictive.

Introduction

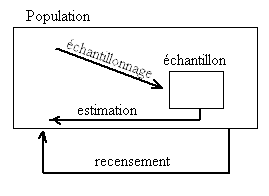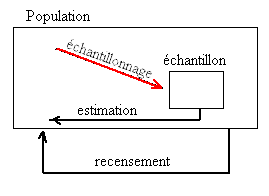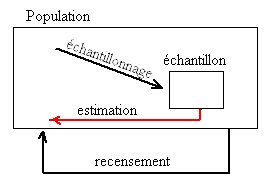
L'inférence statistique fait des propositions sur une population, en utilisant des données tirées de la population avec une certaine forme d'échantillonnage. Étant donné une hypothèse sur une population pour laquelle nous souhaitons faire des inférences, l'inférence statistique consiste à (premièrement) sélectionner un modèle statistique du processus qui génère les données et (seconde) à dériver des propositions à partir du modèle.

Konishi et Kitagawa déclarent que "la plupart des problèmes d'inférence statistique peuvent être considérés comme des problèmes liés à la modélisation statistique". À cet égard, Sir David Cox a déclaré: "La manière dont [la] traduction du problème de la matière dans le modèle statistique est effectuée est souvent la partie la plus critique d'une analyse."

La conclusion d'une inférence statistique est un énoncé statistique. Certaines formes courantes de proposition statistique sont les suivantes:

une estimation ponctuelle, c'est-à-dire une valeur particulière qui se rapproche le mieux d'un paramètre d'intérêt;
une estimation d'intervalle, par exemple un intervalle de confiance (ou une estimation de pool), c'est-à-dire un intervalle construit à l'aide d'un ensemble de données tiré d'une population tel que, lors d'un échantillonnage répété desdits ensembles de données, lesdits intervalles contiendraient la vraie valeur de le paramètre avec la probabilité au niveau de confiance établi;
un intervalle crédible, c'est-à-dire un ensemble de valeurs contenant, par exemple, 95 % de la croyance a posteriori;
rejet d'une hypothèse;
grouper ou classer les points de données en groupes.

Modèles et hypothèses

Toute inférence statistique nécessite certaines hypothèses. Un modèle statistique est un ensemble d'hypothèses liées à la génération des données observées et similaires. Les descriptions des modèles statistiques mettent souvent l'accent sur le rôle des quantités de population d'intérêt, à propos desquelles nous souhaitons faire des inférences. Les statistiques descriptives sont généralement utilisées comme étape préliminaire avant de tirer des inférences plus formelles.

Degré de modèles / hypothèses

Les statisticiens distinguent trois niveaux d'hypothèses de modélisation;

Entièrement paramétrique - Les distributions de probabilité qui décrivent le processus de génération de données sont supposées être entièrement décrites par une famille de distributions de probabilité impliquant uniquement un nombre fini de paramètres inconnus. Par exemple, on peut supposer que la distribution des valeurs dans la population est véritablement normale, avec une moyenne et une variance inconnues, et que les ensembles de données sont générés par un échantillonnage aléatoire "simple". La famille des modèles linéaires généralisés est une classe flexible et largement utilisée de modèles paramétriques.
Non paramétrique - Les hypothèses sur le processus qui génère les données sont beaucoup plus petites que dans les statistiques paramétriques et peuvent être minimales. Par exemple, chaque distribution de probabilité continue a une médiane, qui peut être estimée à l'aide de la médiane de l'échantillon ou de l'estimateur de Hodges-Lehmann-Sen, qui a de bonnes propriétés lorsque les données proviennent d'un échantillonnage aléatoire simple.
Semi-paramétrique: Ce terme implique normalement des hypothèses « intermédiaires » complètes et des approches non paramétriques. Par exemple, une distribution de population peut être supposée avoir une moyenne finie. De plus, on peut supposer que le niveau de réponse moyen dans la population dépend de manière vraiment linéaire d'une certaine covariable (une hypothèse paramétrique) mais ne faire aucune hypothèse paramétrique décrivant la variance autour de cette moyenne (c'est-à-dire de la présence ou de la forme possible de toute hétéroscédasticité). Plus généralement, les modèles semi-paramétriques peuvent souvent être séparés en composants "structurels" et "variations aléatoires". Un composant est traité de manière paramétrique et l'autre de manière non paramétrique.

Importance des modèles/hypothèses valides

Quel que soit le niveau d'hypothèse émis, une inférence correctement calibrée nécessite généralement que ces hypothèses soient correctes; c'est-à-dire que les mécanismes de génération de données ont effectivement été correctement spécifiés.

Des hypothèses incorrectes provenant d'un échantillonnage aléatoire "simple" peuvent invalider l'inférence statistique. Des hypothèses semi- et entièrement paramétriques plus complexes sont également préoccupantes. Par exemple, supposer incorrectement le modèle de Cox peut, dans certains cas, conduire à des conclusions erronées. Des hypothèses incorrectes de normalité de la population invalident également certaines formes d'inférence basée sur la régression. L'utilisation de n'importe quel Le modèle paramétrique est considéré avec scepticisme par la plupart des experts de l'échantillonnage de la population humaine: "la plupart des statistiques d'échantillonnage, lorsqu'elles traitent d'intervalles de confiance, se limitent à des déclarations sur [les estimateurs] basés sur de très grands échantillons." grand, où le théorème central limite garantit que ces [estimateurs] auront des distributions presque normales." En particulier, une distribution normale "serait une hypothèse totalement irréaliste et catastrophiquement imprudente si nous avions affaire à n'importe quel type de population économique". Ici, le théorème central limite stipule que la distribution de la moyenne de l'échantillon "pour de très grands échantillons" a une distribution approximativement normale, si la distribution n'est pas à queue lourde.

Distributions approximatives

Étant donné la difficulté de spécifier des distributions exactes des statistiques de l'échantillon, de nombreuses méthodes ont été développées pour les approximer.

Avec des échantillons finis, les résultats d'approximation mesurent à quel point une distribution limite s'approche de la distribution d'échantillonnage de la statistique: par exemple, avec 10 000 échantillons indépendants, la distribution normale se rapproche (avec une précision à deux chiffres) de la distribution de l'échantillon moyen pour de nombreuses distributions de population, selon la méthode de Berry – Théorème d'Esseen. Cependant, à de nombreuses fins pratiques, l'approximation normale fournit une bonne approximation de la distribution de la moyenne de l'échantillon lorsqu'il y a 10 (ou plus) échantillons indépendants, en fonction des études de simulation et de l'expérience des statisticiens., les statistiques avancées utilisent la théorie de l'approximation et l'analyse fonctionnelle pour quantifier l'erreur d'approximation. Dans cette approche, la géométrie métrique des distributions de probabilité est étudiée; cette approche quantifie l'erreur d'approximation avec, par exemple, la divergence de Kullback-Leibler, la divergence de Bregman et la distance de Hellinger.

Avec des échantillons indéfiniment grands, les résultats limites tels que le théorème central limite décrivent la distribution limite de la statistique d'échantillon, si elle existe. Les résultats limites ne sont pas des déclarations sur les échantillons finis et, en fait, ne sont pas pertinents pour les échantillons finis. Cependant, la théorie asymptotique des distributions limites est souvent invoquée pour travailler avec des échantillons finis. Par exemple, les résultats limites sont souvent invoqués pour justifier la méthode généralisée des moments et l'utilisation d'équations d'estimation généralisées, qui sont populaires en économétrie et en biostatistique. L'amplitude de la différence entre la distribution limite et la vraie distribution (formellement, "l'erreur" de l'approximation) peut être évaluée par simulation.

Modèles basés sur la randomisation

Pour un ensemble de données donné qui a été produit par un plan de randomisation, la distribution de randomisation d'une statistique (sous l'hypothèse nulle) est définie en évaluant la statistique de test pour tous les plans qui auraient pu être générés par le plan de randomisation. Dans l'inférence fréquentiste, la randomisation permet de baser les inférences sur la distribution de randomisation plutôt que sur un modèle subjectif, ce qui est particulièrement important dans l'échantillonnage d'enquête et la conception d'expériences. L'inférence statistique à partir d'études randomisées est également plus simple que de nombreuses autres situations.Dans l'inférence bayésienne, la randomisation est également importante: dans l'échantillonnage par sondage, l'utilisation de l'échantillonnage sans remise assure l'interchangeabilité de l'échantillon avec la population;

La randomisation objective permet des procédures suffisamment inductives. De nombreux statisticiens préfèrent l'analyse basée sur la randomisation des données générées par des procédures de randomisation bien définies. (Cependant, il est vrai que dans les domaines scientifiques avec des connaissances théoriques développées et un contrôle expérimental, les expériences randomisées peuvent augmenter les coûts d'expérimentation sans améliorer la qualité des inférences.) De même, les principales autorités statistiques recommandent les résultats d'expériences randomisées comme permettant des inférences avec une plus grande fiabilité que les études d'observation des mêmes phénomènes. Cependant, une bonne étude observationnelle peut être meilleure qu'une mauvaise expérience randomisée.

L'analyse statistique d'une expérience randomisée peut être basée sur le schéma de randomisation établi dans le protocole expérimental et ne nécessite pas de modèle subjectif.1

Cependant, à tout moment, certaines hypothèses ne peuvent pas être testées à l'aide de modèles statistiques objectifs, qui décrivent avec précision des expériences randomisées ou des échantillons aléatoires. Dans certains cas, ces études randomisées sont inutiles ou contraires à l'éthique.

Analyse basée sur un modèle d'expériences randomisées

Il est de pratique courante de se référer à un modèle statistique, par exemple un modèle linéaire ou logistique, lors de l'analyse des données d'expériences randomisées. Cependant, le schéma de randomisation guide le choix d'un modèle statistique. Il n'est pas possible de choisir un modèle approprié sans connaître le schéma de randomisation. Des résultats sérieusement trompeurs peuvent être obtenus en analysant les données d'expériences randomisées en ignorant le protocole expérimental; Les erreurs courantes incluent l'oubli du verrou utilisé dans une expérience et la confusion de mesures répétées sur la même unité expérimentale pour des répliques indépendantes du traitement appliqué à différentes unités expérimentales.

Inférence de randomisation sans modèle

Les techniques sans modèle fournissent un complément aux méthodes basées sur des modèles, qui emploient des stratégies réductionnistes de simplification de la réalité. Les premiers combinent, font évoluer, assemblent et entraînent des algorithmes en s'adaptant dynamiquement aux affinités contextuelles d'un processus et en apprenant les caractéristiques intrinsèques des observations.

Par exemple, une régression linéaire simple sans modèle est basée sur

un plan randomisé, où les paires d'observations $(X_{1},Y_{1}),(X_{2},Y_{2}),\cdots,(X_{n},Y_{n})$ sont indépendantes et identiquement distribuées (iid), ou
un plan déterministe, où les variables $X_{1},X_{2},\cdots,X_{n}$ sont déterministes, mais les variables de réponse correspondantes $Y_{1},Y_{2},\cdots,Y_{n}$ sont aléatoires et indépendantes avec une distribution conditionnelle commune, c'est-à-dire $P\left(Y_{j}\leq y |X_{j}=x\right)=D_{x}(y)$ , qui est indépendante de l'indice $j$ .

Dans tous les cas, l'inférence de randomisation sans modèle pour les caractéristiques de la distribution conditionnelle commune $D_{x}(.)$ est basée sur certaines conditions de régularité, par exemple, la régularité fonctionnelle. Par exemple, l'inférence de randomisation sans modèle pour la population caractéristique moyenne conditionnelle, $\mu(x)=E(Y|X=x)$ , peut être estimée de manière cohérente par une moyenne locale ou un ajustement polynomial local, sous l'hypothèse qu'elle $\mu(x)$ est lisse. De plus, sur la base de la normalité asymptotique ou du rééchantillonnage, nous pouvons construire des intervalles de confiance pour la caractéristique de la population, dans ce cas la moyenne conditionnelle, $\mu(x)$ .

Paradigmes d'inférence

Différentes écoles d'inférence statistique ont été créées. Ces écoles, ou « paradigmes », ne s'excluent pas mutuellement, et les méthodes qui fonctionnent bien sous un paradigme ont souvent des interprétations attrayantes sous d'autres paradigmes.

Bandyopadhyay et Forster décrivent quatre paradigmes: "(i) statistiques classiques ou statistiques d'erreur, (ii) statistiques bayésiennes, (iii) statistiques basées sur la vraisemblance, et (iv) statistiques basées sur des critères d'information Akaikean". Le paradigme classique (ou fréquentiste), le paradigme bayésien, le paradigme plausible et le paradigme basé sur l'AIC sont résumés ci-dessous.

Inférence fréquentiste

Ce paradigme calibre la plausibilité des propositions en considérant un échantillonnage répété (théorique) d'une distribution de population pour produire des ensembles de données similaires à celui dont nous disposons. En considérant les caractéristiques de l'ensemble de données dans un échantillonnage répété, les propriétés fréquentistes d'une proposition statistique peuvent être quantifiées, bien qu'en pratique cette quantification puisse être difficile.

Exemples d'inférence fréquentiste

p -valeur
Intervalle de confiance
Test de signification de l'hypothèse nulle

Inférence fréquentiste, objectivité et théorie de la décision

Une interprétation de l'inférence fréquentiste (ou inférence classique) est qu'elle n'est applicable qu'en termes de probabilité de fréquence; c'est-à-dire en termes d'échantillonnage répété d'une population. Cependant, l'approche de Neyman développe ces procédures en termes de probabilités antérieures à l'expérience. C'est-à-dire qu'avant d'entreprendre une expérience, on décide d'une règle pour parvenir à une conclusion telle que la probabilité qu'elle soit correcte est suffisamment contrôlée: une telle probabilité n'a pas besoin d'avoir une interprétation d'échantillonnage répété ou fréquentiste. En revanche, l'inférence bayésienne fonctionne en termes de probabilités conditionnelles (c'est-à-dire des probabilités conditionnelles aux données observées),

Les tests de signification fréquentistes et les procédures d'intervalle de confiance peuvent être construits sans tenir compte des fonctions d'utilité. Cependant, certains éléments des statistiques fréquentistes, comme la théorie de la décision statistique, intègrent des fonctions d'utilité. En particulier, les développements fréquentistes de l'inférence optimale (comme les estimateurs sans biais de moindre variance ou les tests uniformément les plus puissants) utilisent des fonctions de perte, qui jouent le rôle de fonctions d'utilité (négatives). Les fonctions de perte n'ont pas besoin d'être énoncées explicitement pour que les théoriciens de la statistique montrent qu'une procédure statistique a une propriété d'optimalité. Cependant, les fonctions de perte sont souvent utiles pour définir des propriétés d'optimisation: par exemple,

Alors que les statisticiens utilisant l'inférence fréquentiste doivent eux-mêmes choisir les paramètres d'intérêt et les estimateurs/statistiques de test à utiliser, l'absence d'utilités manifestement explicites et de distributions a priori a aidé les procédures fréquentistes à être largement considérées comme « objectives ».

Inférence bayésienne

Le calcul bayésien décrit les degrés de croyance en utilisant le « langage » de la probabilité; les croyances sont positives, elles sont intégrées en une seule et obéissent aux axiomes de la probabilité. L'inférence bayésienne utilise les croyances a posteriori disponibles comme base pour faire des propositions statistiques. Il existe plusieurs justifications différentes pour l'utilisation de l'approche bayésienne.

Exemples d'inférence bayésienne

Intervalle crédible pour l'estimation de l'intervalle
Facteurs de Bayes pour la comparaison de modèles

Inférence bayésienne, subjectivité et théorie de la décision

De nombreuses inférences bayésiennes informelles sont basées sur des résumés "intuitivement raisonnables" de la suite. Par exemple, la moyenne postérieure, la médiane et le mode, les intervalles de densité postérieure les plus élevés et les facteurs de Bayes peuvent être motivés de cette manière. Bien qu'il ne soit pas nécessaire d'énoncer la fonction d'utilité d'un utilisateur pour ce type d'inférence, tous ces résumés dépendent (dans une certaine mesure) de croyances antérieures et sont généralement considérés comme des conclusions subjectives. (Des méthodes de pré-construction qui ne nécessitent pas d'apport externe ont été proposées, mais n'ont pas encore été complètement développées.)

Formellement, l'inférence bayésienne est calibrée en référence à une fonction d'utilité ou de perte explicitement énoncée; la « règle de Bayes » est celle qui maximise l'utilité espérée, moyennée sur l'incertitude a posteriori. Ainsi, l'inférence bayésienne formelle produit automatiquement des décisions optimales au sens de la théorie de la décision. Compte tenu des hypothèses, des données et de l'utilité, l'inférence bayésienne peut être effectuée pour pratiquement n'importe quel problème, bien que toutes les inférences statistiques n'aient pas besoin d'une interprétation bayésienne. Les analyses qui ne sont pas formellement bayésiennes peuvent être (logiquement) incohérentes; une caractéristique des procédures bayésiennes qui utilisent des priors appropriés (c'est-à-dire ceux intégrables à un) est qu'ils sont garantis cohérents. doit avoir lieu dans ce cadre théorique de la décision, et que l'inférence bayésienne ne doit pas se terminer par l'évaluation et le résumé des croyances ultérieures.

Inférence basée sur la vraisemblance

La probabilité se rapproche des statistiques en utilisant la fonction de vraisemblance. Certains vérisimistes rejettent l'inférence, considérant les statistiques comme le seul support informatique de la preuve. D'autres, cependant, proposent des inférences basées sur la fonction de vraisemblance, dont la plus connue est l'estimation du maximum de vraisemblance.

Inférence basée sur l'AIC

Le critère d'information d'Akaike (AIC) est un estimateur de la qualité relative des modèles statistiques pour un ensemble de données donné. Étant donné une collection de modèles pour les données, l'AIC estime la qualité de chaque modèle, par rapport à chacun des autres modèles. Ainsi, l'AIC fournit un moyen de sélection du modèle.

L'AIC est basée sur la théorie de l'information: elle fournit une estimation de l'information relative perdue lorsqu'un modèle donné est utilisé pour représenter le processus qui a généré les données. (Ce faisant, il traite du compromis entre la qualité de l'ajustement du modèle et la simplicité du modèle.)

Autres paradigmes d'inférence

Longueur minimale de la description

Le principe de la longueur minimale de description (MDL) a été développé à partir des idées de la théorie de l'information et de la théorie de la complexité de Kolmogorov. Le principe (MDL) sélectionne des modèles statistiques qui compressent au maximum les données; L'inférence procède sans supposer de "mécanismes générateurs de données" ou de modèles de probabilité non falsifiables ou contrefactuels pour les données, comme cela pourrait être fait dans les approches fréquentistes ou bayésiennes.

Cependant, si un "mécanisme de génération de données" existe réellement, alors, selon le théorème de codage de source de Shannon, il fournit la description MDL des données, moyennée et asymptotique. En minimisant la longueur de la description (ou la complexité descriptive), l'estimation MDL est similaire à l'estimation du maximum de vraisemblance et à l'estimation postérieure maximale (utilisant des priors bayésiens à entropie maximale). Cependant, MDL évite de supposer que le modèle de probabilité sous-jacent est connu; Le principe du CDM peut également être appliqué sans supposer que, par exemple, les données proviennent d'un échantillonnage indépendant.

Le principe MDL a été appliqué dans la théorie du codage des communications, la théorie de l'information, la régression linéaire et l'exploration de données.

L'évaluation des procédures inférentielles basées sur MDL utilise souvent des techniques ou des critères de la théorie de la complexité computationnelle.

Inférence fiduciaire

L'inférence fiduciaire était une approche de l'inférence statistique basée sur la probabilité fiduciaire, également connue sous le nom de «distribution fiduciaire». Dans des travaux ultérieurs, cette approche a été décrite comme mal définie, extrêmement limitée dans son applicabilité, voire fallacieuse. Cependant, cet argument revient à montrer que la distribution dite de confiance n'est pas une distribution de probabilité valide et, puisque cela n'a pas invalidé l'application des intervalles de confiance, cela n'invalide pas nécessairement les conclusions tirées des arguments fiduciaux. Une tentative a été faite pour réinterpréter les premiers travaux de Fisher sur l'argument fiducial comme un cas particulier d'une théorie de l'inférence utilisant des probabilités supérieures et inférieures.

Inférence structurelle

S'appuyant sur les idées de Fisher et Pitman de 1938 à 1939, George A. Barnard a développé «l'inférence structurelle» ou «l'inférence fondamentale», une approche qui utilise des probabilités invariantes sur des familles de groupes. Barnard a refondu les arguments derrière l'inférence fiduciale sur une classe restreinte de modèles dans lesquels les procédures « fiduciales » seraient bien définies et utiles. Donald AS Fraser a développé une théorie générale de l'inférence structurelle basée sur la théorie des groupes et l'a appliquée à des modèles linéaires. La théorie formulée par Fraser a des liens étroits avec la théorie de la décision et les statistiques bayésiennes et peut fournir des règles de décision fréquentistes optimales si elles existent.

Sujets d'inférence

Les sujets ci-dessous relèvent généralement du domaine de l'inférence statistique.

Hypothèses statistiques
Théorie de la décision statistique
Théorie de l'estimation
Test d'hypothèse statistique
Examen des opinions en statistiques
Conception d'expériences, analyse de variance et de régression.
Échantillonnage d'enquête
Résumé des données statistiques

Más resultados...