Zero

The zero (0) is a numeral of the even property. It is the numerical sign of null value, which in positional notation occupies the places where there is no significant figure. If it is located to the right of an integer, its value is multiplied by 10; placed to the left, it does not modify it.

Using it as a number, you can perform algebraic operations with it such as addition, subtraction, multiplication, among others. But, since it is the expression of the null value (nothing, nobody, none...), it can give rise to indeterminate expressions or those that lack meaning.

Is the element of the ordered set of integers (ℤ, ≤) that follows –1 and precedes 1.

Some mathematicians consider it to belong to the set of naturals (ℕ) since these can also be defined as the set that allows us to count the number of elements that the others contain sets, and the empty set has no elements, in some studies zero is not considered a natural. When the inclusion or not of zero in natural numbers is relevant, it is specified in the notation, indicating ℕ₀ as the set of natural numbers including zero and ℕ⁺ as the set of natural numbers excluding zero.

The number zero can be represented as any number plus its opposite (or, equivalently, minus itself): X + (–X ) = 0.

Etymology

The word «zero» comes into Spanish from the Italian zero, and this one from the Low Latin zephyrum; this word comes from the translation of the Sanskrit name shunya (empty) to Arabic ṣifr (صفر). The Italian mathematician Fibonacci (c. 1170-1250), who grew up in North Africa and is credited with introducing the decimal system to Europe, already used the term zephyrum in this sense. This would become zefiro in Italian, and then contracted to zero in Venetian. It should be noted that the Italian word zefiro already existed previously, but with the meaning of "west wind", and it came (as we already mentioned) from Low Latin, which in turn took from the Greek zephyrus; this last word may have influenced the spelling used when transcribing the Arabic word ṣifr into Italian. As for the Spanish word "cifra", it is already a direct derivation of ṣifr.

History

Ancient and great civilizations —such as those of Ancient Egypt, Babylon, Ancient Greece and the Mayan Civilization— have documents of a mathematical or astronomical nature showing symbols indicative of the zero value; but due to various peculiarities of their numerical systems, they did not know how to obtain the true benefit of this capital discovery.

In the Egyptian numbering system the sign “-nfr-” was used

to indicate zero (in the Papyrus Boulaq 18, dated around 1700 BC).

Zero first appeared in Babylonia in the 3rd century BCE. C., although its writing on clay tablets dates back to 2000 BC. C. The Babylonians wrote in unfired clay, on flat surfaces or tablets. His notation was cuneiform. In tablets dated in the year 1700 a. C. numerical annotations are seen in their particular form. The Babylonians used a base 60 system. With their system of notation it was not possible to distinguish the number 23 from 203 or 2003, although this ambiguity did not seem to concern them.

About 400 B.C. C., the Babylonians began to place the sign of "two wedges" in the places where in our system we would write a zero, which read "several". The two wedges weren't the only way to show zero positions; on a tablet dated to 700 B.C. C. found in Kish, an ancient city of Mesopotamia to the east of Babylon, used a sign of "three hooks". In other tablets they used a single "hook" and, in some cases, the deformation of this resembles the shape of the zero.

Mayan glyph for zero36 B.C. It is the first documented use of zero using positional notation.

The reverse of step C of the Epi Olmeca culture of Three Zapotes, the second oldest date discovered from the Mesoamerican calendar of the long account. Numbers 7.16.6.16.18 are translated into September 32 years before Christ. It is believed that the glyphs surrounding the date are one of the little surviving examples of epi-olmeca writing.

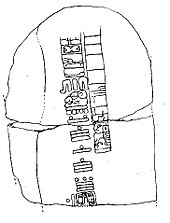
The zero also arose in Mesoamerica and was devised by the Mesoamerican civilizations before the Christian era, by the Mayan culture. It was possibly used earlier by the Olmec culture.

The first documented use showing the number zero corresponds to the year 36 B.C. C., making use of the Mayan numbering. Because of the anomaly introduced in the third place of their positional notation, it deprived them of operational possibilities.

Claudio Ptolemy in the Almagest, written in 130 AD. C., used the value of "empty" or "0". Ptolemy used to use the symbol between digits or at the end of the number. One might think that zero would have taken root then, but the truth is that Ptolemy did not use the symbol as a "number" but considered it a sign of annotation. This use did not spread, as very few adopted it.

The Romans did not use zero. His numbers were letters of his alphabet; to represent figures they used: I, V, X, L, C, D, M, grouping them. For numbers with values equal to or greater than 4,000, they drew a horizontal line over the "number," to indicate that the value was multiplied by 1,000.

Positional Zero

Indian civilization is the cradle of positional notation, almost universally used in the XXI century. It is possible that the Indian mathematician Brahmagupta (VI century) was the first to theorize about the concept of «zero» not only as definition of a null quantity, but as a possible sum for negative and positive numbers. The first evidence of the use of the "Indian zero" is dated to the year 683: a Cambodian inscription from Angkor Wat, carved in stone, which includes the number "605". Other evidence of use dates to around the year 810. The inscriptions from Gwalior are dated to 875-876. Abu Ja'far Mujammad ibn Musa (Al-Khuarismi), in his work entitled "A Treatise on Addition and Subtraction by Calculation of the Indians" explains the principle of positional numbering decimal, indicating the Indian origin of the figures. The tenth figure, which has a rounded shape, is the "zero".

The Arabs transmitted it through the Maghreb and Al-Andalus, later passing to the rest of Europe. The first manuscripts showing the Indian figures (then called “Arabs”) come from northern Spain and are from the X century: the Codex Vigilanus and the Codex Aemilianensis. Zero does not appear in the texts, since the calculations were made with an abacus, and its use was apparently not necessary.

Although the first uses of the zero are attributed in France, or to the controversial Pope Silvestre II, around the year 1000, most of the references indicate that the zero (called zefhirum) was introduced to Europe by the Italian mathematician Fibonacci in the 12th century, showing Arabic algebra in its Liber abaci (The book of the abacus), although due to the ease of the new system, the ecclesiastical authorities branded it magical or demonic.

The Church and the caste of professional calculators — mostly clergymen, who used the abacus — were in direct opposition, vetoing the new algebra, in some places as late as the XV.

Representations of zero

Zero is represented in Western texts by the number "0". Since the XX century, and especially with the development of computing, it is common for this sign to appear cut by a slash (/), a new notation that avoided confusion with the spelling of the letter «o». Until recently, the disjunctive conjunction "or" had to have a tilde: "ó", when it was written between figures so as not to be confused with the numerical sign 0. Currently, this rule is not in force.

Graphical representation of the zero value

In Cartesian coordinates, the origin of coordinates is associated with the value 0 (zero).

Zero and natural numbers

Zero, being a special numerical concept, was not included in the set of natural numbers ℕ, by convention. It was represented as ℕ₀, the set of natural numbers when it includes zero, so it is possible to find many books where the authors do not consider zero as a natural number. In fact, there is still no consensus on the matter.

Some mathematicians find it convenient to treat it like the other natural numbers, hence the discrepancy. From a historical point of view, zero appears so late that some do not believe it is fair to call it natural.

Mathematical operations with zero

Zero in the sum

In addition, zero is the neutral element; that is, any number a added with 0 returns to a. Example: 25 + 0 = 25. That is, every number added with 0 is the same number.

Zero in subtraction

In subtraction, zero is the neutral element; that is, any number a subtracted with 0 returns to a, except when zero is the minuend, in which case -a is returned. Examples:

37 - 0 = 37

0 - 37 = -37

Zero in multiplication

In the product, zero is the absorbing element; any number operated on 0 gives 0. Example: 25 × 0 = 0

Zero in division

Zero can be divided by other numbers, in which case it is the absorbing element (example: 0:25 = 0). Zero cannot divide any number.

Division by zero in real numbers

In the real numbers (even in the complex ones) the division by zero is an indeterminacy; So the expressions:

⁸♪₀; ⁰♪₀

make no sense.

Intuitively, it means that it doesn't make sense. "Distribute" 8 apples to children in an empty classroom. Nor does it make 'sense', to distribute 0 tickets among zero people: nothing among nobody.

Mathematically, zero is the only real number by which it cannot be divided. That is why 0 is the only real that does not have a multiplicative inverse.

Example:

^x♪₂ = x · ¹♪₂ (right).

^x♪₀ = x · ¹♪₀ (incorrectly because ¹♪₀ It's not a real number.

Zero in the division of limits

In mathematical analysis there are definitions of different types of limits. For example:

limt→ → 0t2t=0{displaystyle lim _{trightarrow 0}{frac {t^{2}{t}{t}}=0},

limt→ → 0tt=1{displaystyle lim _{trightarrow 0}{frac {t}{t}{t}}}=1},

limt→ → 0tt2=∞ ∞ {displaystyle lim _{trightarrow 0}{frac {t}{t^{2}}}}{infty }.

However, if each numerator and denominator are analyzed separately, the limit of all of them is zero. That is why it is said that ⁰⁄₀ is indeterminate, since results can be obtained as different as infinity, one or zero.

Zero on Empowerment

• Yeah. a It's different from 0, then a0=1.{displaystyle a^{0}=1. !
• Yeah. n is greater than 0, then 0n=0.{displaystyle 0^{n}=0. !

The value 00{displaystyle 0^{0}} is not defined as power, but depending on context or comfort you can choose one of the results by definition. Some scientific calculators give 1 as a result.

In the context of limits, 00{displaystyle 0^{0}} is an indetermination because the limits of powers such that the base and exponent limits separately are zero, can end up giving anything.

Parity

In the set of integers, ℤ the 0 is an even number; satisfies the definition of parity, as well as all the characteristics of even numbers.

The zero is a Number pair, located between two odd numbers (the –1 and 1).

Zero in Euler's Identity

Zero, along with the numbers 1, π, i, e are related in the famous Euler Identity:

e^iπ + 1 = 0

Advanced Mathematics

In other branches of mathematics, especially in algebra, elements of other sets that are very different from the real ones are called «zero» and are also symbolized with «0». This is the case of the null vector in the set of vectors of the plane or space. In general, the neutral element of an abelian group is said to be zero.

Digital systems

The 0 is associated with the "off" position in positive logic (1 is associated with the "on" position) and is one of the two digits (0 and 1) of the binary system.

Absolute zero

Absolute zero is, in the field of physics, the lowest temperature that matter can theoretically reach. This temperature gives rise to the Kelvin scale, which establishes said temperature as 0 K. Its equivalence in degrees Celsius is –273.15 °C.