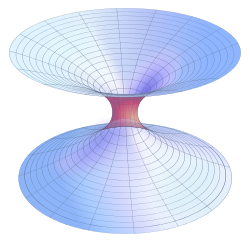
Wormhole

Scheme of a wormhole that technically allows the journey through time. If one of the two ends of the bridge crossed by the green line is on the move, follow the red route and return to the starting point according to the opposite sense of the green route could allow back in time, as the space-time represented would have closed temporary curves.

In physics, a wormhole, also known as an Einstein-Rosen bridge, is a hypothetical structure associated with a space-time whose topology is multiply connected. Such a structure is a possible solution of Einstein's field equations of general relativity, essentially consisting of a bridge across space and time. A wormhole has at least two ends connected to a single throat, through which matter could travel. To date, no evidence has been found that known space-time contains structures of this type, so it is currently only a theoretical possibility in physics.

When a red supergiant star explodes, it spews matter outward, so it ends up smaller and becomes a neutron star. But it can also happen that it is compressed so much that it absorbs its own energy inside and disappears, leaving a black hole in the place it occupied. This hole would have such a great gravity that not even electromagnetic radiation could escape from inside it. It would be surrounded by a spherical boundary, called the event horizon. Light would cross this boundary to enter, but could not exit, so the hole seen from great distances would have to be completely black (although Stephen Hawking postulated that certain quantum effects would generate so-called Hawking radiation). Inside the hole, astrophysicists conjecture that a kind of bottomless cone is formed. In 1994, the Hubble Space Telescope detected the presence of a very dense one in the center of the elliptical galaxy M87, since the high acceleration of gases in that region indicates that there must be an object 3.5 billion times more massive than the Sun. Finally, this hole could eventually engulf the entire galaxy.

The hypothesis suggests that, on one side, there is a black hole that absorbs matter, but, on the other side, there would be a white hole that would expel everything that the black swallows.

The first scientist to warn of the existence of wormholes was the Austrian Ludwig Flamm, in 1916. In this sense, the wormhole hypothesis is an update of the nineteenth-century theory of a fourth spatial dimension that supposed —for example—given a toroidal body in which the three commonly perceptible spatial dimensions could be found, a fourth spatial dimension that would abbreviate distances and thus travel times. This initial notion was put forward in a more scientific way in 1921 by the German mathematician Hermann Weyl, however, he did not use the term "wormhole" to describe it. (he spoke of & # 34; one-dimensional tubes & # 34;), when he related his analyzes of the mass in terms of the energy of an electromagnetic field with Albert Einstein's theory of relativity published in 1916.

Currently, string theory admits the existence of more than three spatial dimensions (see hyperspace), but those extra dimensions would be compacted to subatomic scales (according to the Kaluza-Klein theory), so it seems very difficult (if not impossible) to take advantage of them to travel in space and time.

Origin of name

The term "wormhole" was introduced by the American theoretical physicist John Wheeler in 1957 (inspired by the work of Hermann Weyl) and through an article co-written with Charles Misner:

This analysis compels us to consider situations... where there is a net flow of force lines, through what the topologists would call "toroidal decomposition" of space with multiple connections, and what the physicists might excuse themselves to call more vividly a "worm hole".

Charles Misner and John Wheeler in Annals of Physics

It comes from the following analogy used to explain the phenomenon: if the universe is the skin of an apple, and a worm travels on its surface, the distance from a point on the apple to its antipode is equal to half the circumference of the apple, as long as the worm remains on the surface of the apple. But if the worm were to dig a hole directly through the apple instead, the distance it would have to travel would be considerably less, since the closest distance between two points is a straight line joining them.

Types of wormholes

• Them Intrauniverse wormholes connect a position of a universe with another position of the same universe in a different time. A wormhole should be able to connect distant positions in the universe by spacetime prayers, so that it would allow to travel between them in a lesser time than the one that would take the journey through normal space.
• Them Interuniverse wormholes They associate a universe with another different one and are called "Schwarzschild wormholes". This allows speculation about whether such wormholes could be used to travel from one universe to another parallel. Another application of a wormhole could be the journey in time. In that case, it would be a shortcut to move from a timeless point to another. In string theory, a wormhole is seen as the connection between two D-branas, where the mouths are associated with the branas and connected by a flow tube. Worm holes are believed to be a part of quantum or timeless foam.

Other classification:

• Euclid worm holes, studied in particle physics.
• Lorentz wormholes, mainly studied in general relativity and in semi-classic gravity. Among these are the piercing wormholes, a special type of Lorentz wormhole that would allow a human being to travel from one side to the other of the hole.

Until now, different types of wormholes have been theorized, mainly as mathematical solutions to the question. Essentially, these wormhole types are:

• The Schwarzschild wormhole supposedly formed by a black hole in Schwarzschild, which is considered to be unbearable.
• The wormhole supposedly formed by a black hole of Reissner-Nordstrøm or Kerr-Newman, which would be frank, but in one direction, and could contain a wormhole of Schwarzschild.
• The wormhole of Lorentz, which has negative mass and is estimated to be frank in both directions (paste and future).

Schwarzschild wormholes

Schwarzschild wormhole diagram.

Lorentz wormholes, known as Schwarzschild wormholes or Einstein-Rosen bridges, are nexus connecting areas of space that can be modeled as vacuum solutions in Einstein's field equations by union of a model of a black hole and one of a white hole. This solution was found by Albert Einstein and his partner Nathan Rosen, who first published the result in 1935. However, in 1962, John A. Wheeler and Robert W. Fuller published a paper in which they reported the proof that this type of Wormhole is unstable and would disintegrate instantly as soon as it forms.

Before the stability problems of Schwarzschild wormholes became apparent, it was proposed that quasars could be white holes, thus forming the end zones of wormholes of this type. However, recent research rules out that quasars are comparable to white holes.

Schwarzschild wormholes inspired Kip Thorne to imagine transiting through them by clamping down their throat and opening it with exotic matter (negative mass and energy).

Practicable Wormholes

Image of a practical wormhole (which can be crossed) that would connect the area in front of the University of Tubinga physics institute with the dunes close to Boulogne-sur-Mer, in northern France. The image has been recreated by a software 4D-ray trace, in a Morris-Thorne metric, although gravitational effects on wavelength have not been simulated.

Practable Lorentz wormholes, also called traversables, would make it possible to travel not only from one part of the universe to another, but even from one universe to another. Wormholes connect two points in space-time, so they would allow travel in both space and time. In the theory of general relativity, the possibility of traversing wormholes was first demonstrated by Kip S. Thorne and his graduate Mike Morris in a paper published in 1988. The type of traversable wormhole they discovered would stay open. by a kind of spherical shell of exotic matter called a Morris-Thorne wormhole. Subsequently, other types of traversable wormholes have been discovered, such as one that is held open by cosmic strings, previously hypothesized by Matt Visser in an article published in 1989.

Theoretical basis

Definition

The topological definition of a wormhole is far from intuitive. A wormhole is said to exist in a compact region of space-time when its boundary set is topologically trivial, but its interior is not simply connected. Formalizing this idea leads to definitions such as the following, taken from Matt Visser's Lorentzian Wormholes,:

If a Lorentz space-time contains a compact region Ω and if the topology of Ω is of the form Ω ~ R x Σ, where Σ is a non-trivial 3-manifold topology whose boundary has a topology of the form dΣ ~ S², and if in addition the Σ hypersurfaces are of spatial type, then the Ω region contains a quasi-permanent intrauniversal wormhole.

Characterizing interuniverse wormholes is more difficult. For example, we can imagine a newborn universe connected to its parent by a narrow navel. One could think of the navel as the throat of a wormhole, through which space-time is connected.

Plausibility

Lorentz wormholes are known to be possible within general relativity, but the physical possibility of these solutions is uncertain. It is even unknown if the theory of quantum gravity, which is obtained by condensing general relativity with quantum mechanics, would allow the existence of these phenomena. Most of the known solutions of general relativity that allow traversed wormholes to exist require the existence of foreign matter, a theoretical substance that contains energy of negative density. However, it has not been mathematically proven that this is an absolute requirement for traversed wormholes of this type, nor has it been established that exotic matter cannot exist.

It is not yet empirically known whether wormholes exist. A solution to the equations of general relativity (such as the one found by L. Flamm) that would make the existence of a wormhole possible without the requirement of exotic matter—a theoretical substance that would possess a negative energy density—has not been found. still verified. Many physicists, including Stephen Hawking (with his chronological protection conjecture), believe that because of paradoxes (or is it aporias?) time travel through a wormhole would imply that something fundamental exists in the laws of the physics that prevents such phenomena (see cosmic censorship).

In March 2005, Amos Ori envisioned a wormhole that allowed time travel without requiring exotic matter and satisfying all energetic conditions. The stability of this solution is uncertain, so it remains unclear whether infinite precision would be required for time travel to form and enable it, and whether quantum effects would protect the chronological sequence of time in this case.

Wormhole metrics

Wormhole metric theories describe the space-time geometry of a wormhole and serve as theoretical models for time travel. A simple example of the metric of a traversed wormhole could be the following:

ds2=− − c2dt2+dl2+(k2+l2)(dθ θ 2+without2 θ θ dφ φ 2){displaystyle ds^{2}=-c^{2}{text{d}}{2+}{text{d}}{2}+(k^{2}+l^{2})({text{d}}}}{theta ^{2}+sin ^{2}{2}theta ,{text{d}}{phi ^{2}{2}{2}}{2}{2}

One type of non-traversed wormhole metric is the Schwarzschild solution:

ds2=− − (1− − 2GMc2r)dt2+dr21− − 2GMc2r+r2(dθ θ 2+without2 θ θ dφ φ 2){displaystyle ds^{2}=-left(1-{frac {2GM}{c^{2}r}{2}{right){text{d}}{2}{2}{frac}{text{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{

First represented by Ellis as a special case of Ellis drainage.

The Einstein-Rosen Bridge was described in an article published in July 1935.

For the static spherically symmetric Schwarzschild solution.

ds2=− − 11− − 2mrdr2− − r2(dθ θ 2+without2 θ θ dφ φ 2)+(1− − 2mr)dt2{displaystyle ds^{2}=-{frac {1}{1-{frac {2m}{r}}}dr^{2}-r^{2}(dtheta ^{2}{2}{2}{2}{2}{2}{2}theta ,dphi ^{2})+(1-{frac {2m}{2m}{r}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}

(ds{displaystyle ds} = appropriate time, c{displaystyle c} = (1)

If one replaces r{displaystyle r} for u{displaystyle u} according to u2=r− − 2m{displaystyle u^{2}=r-2m}

The four-dimensional space is mathematically described by two congruent parts or "sheets", which correspond to u{displaystyle u} ▪ u{displaystyle u} 0, which are joined by a hyperplane r=2m{displaystyle r=2m} or u{displaystyle u} = 0 in which g{displaystyle g} disappear. We call such a connection between the two leaves a "bridge" (authors=A. Einstein, N. Rosen, "The Particle Problem in the General Theory of Relativity")

For the combination of gravity and electricity, Einstein and Rosen derived the Schwarzschild symmetric spherical solution

φ φ 1=φ φ 2=φ φ 3=0,φ φ 4=ε ε 4,{displaystyle phi _{1}=phi _{2}=phi _{3}=0,phi _{4}={frac {epsilon }{4}}},}

ds2=− − 1(1− − 2mr− − ε ε 22r2)dr2− − r2(dθ θ 2+without2 θ θ dφ φ 2)+(1− − 2mr− − ε ε 22r2)dt2{displaystyle ds^{2}=-{frac {1}{(1-{frac}{2m}{r}}{r}-{frac {epsilon ^{2}{2r}{2}{2}}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}}{2}{2}}{2}{2}}{2}{2}{2}{2}{2}{2}}}}}{2}}{2}{2}{2}{2}}}{

(ε ε {displaystyle epsilon } = electric charge)

Field equations without denominators in the case where m{displaystyle m} = 0 can be written

φ φ μ μ .. =φ φ μ μ ,.. − − φ φ .. ,μ μ {displaystyle phi _{mu nu }=phi _{munu }-phi _{numu }}}}

g2φ φ μ μ .. ;σ σ g.. σ σ =0{displaystyle g^{2}phi _{mu nu;sigma }g^{nu sigma }=0}

g2(Rik+φ φ iα α φ φ kα α − − 14gikφ φ α α β β φ φ ab)=0{displaystyle g^{2}(R_{ik}+phi _{ialpha }phi _{k}^{alpha }-{frac {1}{4}}}}}g_{ik}phi _{alpha beta }phi {ab})=0}

To remove the singularities, if replaced r{displaystyle r} for u{displaystyle u} according to the equation:

u2=r2− − ε ε 22{displaystyle u^{2}=r^{2}-{frac {epsilon ^{2}}{2}}}{2}}}}{2}}}

and with m{displaystyle m} = 0 obtained

φ φ 1=φ φ 2=φ φ 3=0,φ φ 4=ε ε /(u2+ε ε 22)12{displaystyle phi _{1}=phi _{2}=phi _{3}=0,phi _{4}=epsilon /(u^{2}+{frac {epsilon ^{2}{2}}{2}}}{frac {1}}}}}}}

ds2=− − du2− − (u2+ε ε 22)(dθ θ 2+without2 θ θ dφ φ 2)+(2u22u2+ε ε 2)dt2{displaystyle ds^{2}=-du^{2}-(u^{2}+{frac {epsilon ^{2}}{2}}})(dtheta ^{2}{2}{2}{2}{2}{2}{2}{2}{2}{2 ^{2}{2}{2}{2}{2}{2 ^{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2

The solution is free of singularities for all finite points in the space of the two leaves (authors=A. Einstein, N. Rosen, "The Particle Problem in the General Theory of Relativity")

Wormholes and time travel

Artistic interpretation of a wormhole as should be seen by an observer who was going through the horizon of events of a wormhole of Schwarzschild, which is similar to a black hole of Schwarzschild, but with the peculiarity of possessing, instead of the region where gravitational singularity (in the case of the black hole), an unstable path to a white hole that would exist in another universe (see multiverse). This region is inaccessible in the case of a Schwarzschild wormhole as the bridge between the black hole and the white hole would always collapse before the observer has time to get through it. See White Holes and Wormholes for a more technical discussion and an animation that represents what an observer would see going through a Schwarzschild wormhole.

In theory, a wormhole could allow time travel through space-time. This could be done by accelerating the end of a wormhole to a relatively high velocity relative to its other end. Relativistic time dilation would result in an accelerated wormhole mouth aging more slowly than the stationary mouth, as seen by an outside observer, similar to what is seen in the twin paradox. However, time passes through the wormhole differently than outside, so the synchronized clocks in each mouth will stay in sync for someone traveling through the wormhole, no matter how much the mouths move. This means that anything entering the wormhole's accelerating mouth could exit the stationary mouth at a point in time prior to its entry if the time dilation has been sufficient.

For example, suppose that two clocks in both mouths show the year 2000 before accelerating one of the mouths and, after accelerating one of the mouths to speeds close to the speed of light, we bring both mouths together when in the accelerated mouth the The clock shows the year 2017 and the stationary mouth shows the year 2013. In this way, a traveler who entered through the accelerated mouth at this moment would exit through the stationary mouth when his watch also marked the year 2013, in the same region of space. but four years in the past. Such a wormhole configuration would allow a worldline particle of space-time to form a closed space-time loop, known as a closed time-like curve. The course through a wormhole through a closed time-like curve causes a wormhole to have characteristics of a time gap.

It is considered nearly impossible to turn a wormhole into a "time machine" in this way. Some analyzes using semiclassical approximations that incorporate quantum effects in general relativity indicate that a feedback of virtual particles would circulate through the wormhole with a continuously increasing intensity, destroying it before any information could pass through it, in accordance with what is postulated by the wormhole. chronological protection guess. This has been questioned, suggesting that the radiation would scatter after traveling through the wormhole, thus preventing its infinite accumulation. Kip S. Thorne has a debate about it in his book Black Holes and Time Warps. The so-called Ring has also been described. Romano, a configuration made up of more than one wormhole. This ring seems to allow a closed timeline with stable wormholes when analyzed under the prism of semiclassical gravity, but without a complete theory of quantum gravity it is not yet possible to know if this semiclassical approximation is applicable in this case.

Travel at speeds greater than that of light

Special relativity only applies locally. Wormholes — if they actually existed — would theoretically allow superluminal (faster-than-light) travel ensuring that the speed of light is not locally exceeded at any time. When traveling through a wormhole, the speeds are subluminal (below the speed of light). If two points are connected by a wormhole, the time it takes to go through the wormhole would be less than the time it takes for a ray of light to travel around the outside of the wormhole. However, a ray of light traveling through the wormhole would always hit the traveler. As an analogy, going around the side of a mountain to the opposite side at full speed can take longer than going under the mountain through a tunnel at a slower speed, since the drive is shorter.

Subatomically, the existence of a quantum foam or a space-time foam is hypothesized, advancing with the conjecture, the possibility of existence of wormholes in it is hypothesized, although if they existed they would be highly unstable and only they could be stabilized by investing enormous amounts of energy (for example with gigantic particle accelerators that can create a quark-gluon plasma).

Interuniversal journey

A possible resolution of the paradoxes resulting from time travel through wormholes is based on the many worlds interpretation of quantum mechanics.

In 1991, David Deutsch showed that quantum theory is fully consistent (in the sense that the so-called density matrix can be free of discontinuities) over time periods with closed time curves. showed that such a closed time curve model may have internal inconsistencies, as it will lead to strange phenomena such as the distinction of non-orthogonal quantum states and the distinction of proper and improper mixing. Consequently, the positive feedback loop is avoided destruction of virtual particles circulating through a wormhole time machine, a result indicated by semi-classical calculations. A particle that returns from the future does not return to its home universe but to a parallel universe. This suggests that a wormhole time machine with an extremely short time skip is a theoretical bridge between contemporary parallel universes.

Because a wormhole time machine introduces a type of nonlinearity into quantum theory, this type of communication between parallel universes is consistent with Joseph Polchinski's proposal for an Everett telephone > (named after Hugh Everett) in Steven Weinberg's formulation of nonlinear quantum mechanics.

The possibility of communication between parallel universes has been called interuniversal travel.