White noise
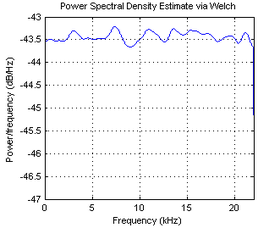
The white noise or white disturbance is a random signal (stochastic process) that is characterized by the fact that its signal values at two different times are not correlated statistics. As a consequence, its power spectral density (PSD) is a constant, i.e. its graph is flat. This means that the signal contains all frequencies and they all show the same power. The same phenomenon occurs with white light, hence the name.
It is a random noise that has the same power spectral density throughout the entire frequency band. Since white light is one that contains all frequencies of the visible spectrum, white noise derives its name from also containing all frequencies, but sound.
White noise is a non-correlative signal, that is, on the time axis the signal takes values without any relation to each other. When it is said that it has a flat power spectral density and needs help, with a theoretically infinite bandwidth, it is that in a frequency spectral graph after having performed a Fourier spectral decomposition, in the rapture
frequency domain we would see all components with the same amplitude, making the effect of a continuous line parallel to the horizontal axis.
If the PSD is not flat, then the noise is said to be "colored" (correlated). Depending on the shape of the noise PSD graph, different colors are defined.
Examples
The attached black and white image depicting the so-called "electronic snow" It is white noise, its pixels do not correlate with each other and therefore its power spectral density is constant. If the image were in color, then the "snow" it would be random colors. This image is what you see on an analog TV screen when it is not tuned to a channel. The signal that the demodulator then receives can be considered white noise, since it is the result of adding the electromagnetic noise of the radio channel, that which is generated by the television's own electronic circuits, the multiple low-intensity interferences, all of which are independent of each other, among other signs. In the latter case, the "snow" it would not remain static, but would constantly change over time, because the television signal is a video signal, consisting of a succession of images (25 frames per second for European standards and 30 for American ones).
Mathematical definition
White noise is a particular case of WSS stochastic process in which random variables that form it are not correlated. I mean, if you have a stochastic process w(k){displaystyle w(k)} WSS (which we will assume in discreet and real time, in an equivalent way for continuous time processes), must then occur that:
- μ μ w=E{w(k)!=0{displaystyle mu _{w}=mathbb {E}{w(k)}=0}
- Rww(Δ Δ )=E{w(k)w(k− − Δ Δ )!=σ σ 2δ δ (Δ Δ ){displaystyle R_{www}(Delta)=mathbb {E} {w(k)w(k-Delta)}=sigma ^{2}delta (Delta)}}
If, instead of having the probability distribution of the process, what we have is a temporary realization of it in the form of a column vector w{displaystyle mathbf {w} } (the most common), then the previous equations will normally be expressed in a matrix form
- μ μ w=E{w!=0{displaystyle mu _{w}=mathbb {E}{mathbf {w}=0}
- Rww=E{wwT!=σ σ 2I{displaystyle R_{www}=mathbb {E} {mathbf {w} mathbf {w} ^{T}}=sigma ^{2}mathbf {I} }} }
Since the process is not correlated, its self-relation function is a delta and its spectral power density (PSD, Power Spectral Density) Sxx(f){displaystyle S_{xx}(f)} It's a constant.
- Sxx(f)=TF{Rww(Δ Δ )!=TF{σ σ 2δ δ (Δ Δ )!=σ σ 2{displaystyle S_{xx}(f)={text{TF}{R_{www}(}{Delta)}={text{TF}}{sigma ^{2}delta (Delta)}=sigma ^{2}}
As the PSD is constant, the signal is not band limited and its power is -theoretically- infinite. In practice, a signal is considered to be white if its PSD is constant in the frequency band of interest in the application. For example, if it is an audio application, the noise will be white if its spectrum is flat between 20 Hz and 20 kHz, which is the frequency band that is audible to the human ear.
In any stochastic process there are always two components:
- an innovative component, which cannot be predicted by linear prediction and which represents entropy, uncertainty, chaos, which cannot be predicted in any way;
- a redundant component that is possible to predict and, therefore, to eliminate (there are based on signal lossless compression techniques such as ADPCM or, more specifically for voice signals, the G.721 standard).
The PSD is the Fourier transform of the autocorrelation function, and since this is a one-to-one mathematical transformation, it is seen that the autocorrelation function and the PSD contain basically the same information about a signal. They are two different ways of looking at the same thing: the degree of entropy of a signal. The entropy of a signal in this case can be seen as a measure of how flat its spectrum is. A signal whose spectrum is not flat is said to be "colored" (autocorrelated or having redundancy).
White noise is a completely innovative process, chaotic, has no redundancy and therefore cannot be compressed.
Analysis and synthesis of colored WSS stochastic processes
You can also see white noise as the residue left after all redundancy is removed from a colored WSS stochastic process. In fact, it is possible to show that any Wide-Sense Stationarity (WSS) process can be obtained by filtering white noise with an all-pole filter (AR model), with a filter all zeros (MA model) or with a filter of poles and zeros (ARMA model).
The following diagram filters white noise w(t){displaystyle w(t)} using linear filter H{displaystyle H}, getting the process out x(t){displaystyle x(t)} colored (the filter H{displaystyle H} introduces correlation between process samples w(t){displaystyle w(t)})
Making Linear Prediction About x(t){displaystyle x(t)}, you get the filter H− − 1{displaystyle H^{-1}, which is the reverse filter (convolution filter) H{displaystyle H} and that allows, after adjusting the process media, to get back the original white noise process w(t){displaystyle w(t)}.
These techniques are of great importance in signal processing. The adaptive filtering is used to study the stability of adaptive algorithms for IIR filters. In voice encoding, the vocoder codecde at no time transmits the signal samples, but a bit that decides whether the fonema is deaf/sound and then the parameters of the linear prediction model for each case (filter H− − 1{displaystyle H^{-1} the diagram). With this technique you can codify the voice with rates as low as 2.4 kbps and with a sufficiently intelligible quality.
Applications
Signal Processing
In general, white noise has many applications in signal processing:
- It serves to determine the transfer function of any linear and invariant system with time (LTI, Linear Time Invariant). For example, in architectural acoustics the transfer function is used to measure acoustic insulation and room reverberation.
- In audio synthesis (electronic music) it is used to synthesize the sound of percussion instruments, or deaf phonemes: /s/, /t/, /f/, etc.
- It can also be used to improve the convergence properties of certain adaptive filter algorithms by injecting a small white noise signal at some point of the system.
Generation of random numbers
White noise generated by certain natural or artificial physical processes is used as a basis for the generation of quality random numbers, since it is, as already stated, a source of entropy.
Use in emergency vehicles
Some emergency vehicles use it because it is easy to distinguish from background noise and it is not masked by echo, making it easier to locate it in space.
Use in humans
White noise can be used to disorient people before interrogation and as a sensory deprivation technique.[citation required]
On the other hand, low-intensity white noise can promote relaxation and sleep, by making the hearing threshold level reach its maximum speed, so that, using this type of background noise, the most intense auditory stimuli they are less able to activate the cerebral cortex during sleep. Thus, some people manage to fall asleep faster if they have the television on with a moderate volume, for example. In specialized stores you can buy compact discs with long sequences of white noise, as well as electromechanical devices that make use of the principle of noise white to "mask out" sudden and annoying noises.
White noise can be assembled inside electrical devices, which are distributed as devices to be able to fall asleep, since it emits a wave frequency, which makes our brain relax, in addition to masking harmful noises. Let's not forget that sound intensities above 60 decibels can be harmful to health. White noise has also been used to camouflage snoring and successfully for people with tinnitus. In work environments, white noise is used so that certain conversations are not heard, thus maintaining confidentiality.