White dwarf
A white dwarf is a stellar remnant that is generated when a star with a mass less than 10 solar masses has used up its nuclear fuel, and has ejected much of this mass into a planetary nebula. In fact, it is a stage of stellar evolution that 97% of the stars we know of will go through, including the Sun. White dwarfs are, along with red dwarfs, the most abundant stars in the universe. Physicist Stephen Hawking, in the glossary of his well-known work History of Time, defines the white dwarf as follows:
Cold star stable, maintained by repulsion due to the principle of electron exclusion.Hawking, Stephen: History of time
Composition
White dwarfs are composed of atoms in the plasma state; Since thermonuclear reactions no longer take place in its core, the star has no energy source to balance the gravitational collapse, so the white dwarf compresses in on itself due to its own weight. The distance between the atoms within it decreases radically, so the electrons have less space to move (in other words, the density increases a lot, up to orders of 106 g/cm³, a ton per cubic centimeter and even more). At these densities, the Heisenberg uncertainty principle and the Pauli exclusion principle come into play for electrons, which are forced to move at very high speeds, generating the so-called electronic degeneracy pressure, which is what effectively opposes the collapse of the star. This electronic degeneracy pressure is a radically different phenomenon from thermal pressure, which is what generally maintains "normal stars." The densities mentioned are so enormous that a mass similar to that of the Sun would fit into a volume like that of the Earth (which would give a density of about 2 t/cm³), and are surpassed only by the densities of neutron stars and of black holes. White dwarfs emit only stored thermal energy, and therefore have very faint luminosities.
Low-mass stars with intermediate intensity (masses less than 1/8 - 1/10 solar masses), upon completion of hydrogen fusion during their lifetime on the main sequence, expand as red giants, and proceed to merge helium into carbon and oxygen into its core. If the red giant is not hot enough to fuse carbon and oxygen in turn, its core is compressed by gravity and its envelope is ejected in a series of thermal pulses during the giant phase in the asymptotic branch, producing thus a planetary nebula that surrounds a stellar remnant: the white dwarf.
99% of white dwarfs are basically made up of carbon and oxygen, which are the residues of helium fusion. However, on the surface is a layer of compressed and partially degenerate hydrogen and helium, which forms the atmosphere of the white dwarf. Only a few are formed entirely by helium, since it has not been burned, or by oxygen, neon, and magnesium, products of the nuclear burning (fusion) of carbon.
Newly formed, white dwarfs have very high temperatures, but since they do not produce energy, they gradually cool down. In theory, white dwarfs will cool over time until they no longer emit detectable radiation, at which time they become black dwarfs. However, the cooling process is so slow that the age of the universe since the Big Bang is too short to host, at this time, one of these black dwarfs. In fact, the coldest known white dwarfs have temperatures of several thousand K. The term white dwarf was coined by Willem Luyten in 1922, although the more appropriate name for objects of this size is nature is that of degenerate stars.
History of its discovery
The first white dwarf was discovered in the 40 Eridani triple star system, which is comprised of the main sequence star 40 Eridani A orbiting the binary system formed by the white dwarf 40 Eridani B, and 40 Eridani C, a dwarf main sequence red. Such a binary system was discovered by William Herschel on January 31, 1783., p. 73 The same binary star was later observed by Friedrich Georg Wilhelm von Struve and Otto Wilhelm von Struve in 1825 and 1851 respectively. In 1910, Henry Norris Russell, Edward Charles Pickering, and Williamina Fleming discovered that, at Despite being a dim star, 40 Eridani B was of spectral type A, or white. The spectral type of 40 Eridani B was officially confirmed in 1914 by Walter Adams.
During the 19th century, techniques for measuring the position of stars became precise enough to be able to detect very small changes in the position of some of them. Friedrich Bessel, in 1844, using these techniques, perceived that the stars Sirius (α Canis Majoris) and Procyon (α Canis Minoris) were changing their positions, so he deduced that these changes in position were due to a star that had been invisible until then. Bessel estimated that the period of this star would be approximately half a century. C.H.F.Peters calculated an orbit for this star in 1851.
The mentioned star is none other than Sirius B, also known as the Cub, the second white dwarf discovered. It has a surface temperature of about 25,000 K, which includes it within the hot stars. On January 31, 1862, Alvan Graham Clark observed a previously unseen species of dark star near Sirius, which was later identified as the star predicted by Bessel. Regardless, Sirius B turned out to be 10,000 times less luminous than the main star Sirius A. Since it had to have a high brightness per unit area, Sirius B had to be much smaller than Sirius A. calculations determined a radius approximately equal to that of the Earth. Analysis of the orbit of the Sirius star system showed that the mass of this strange star was approximately the same as that of the Sun. This implied that Sirius B must be hundreds of times denser than lead, something that could not be explained hydrostatically.. The mystery remained unsolved for quite some time, with Sirius B being considered an unexplainable oddity. Walter Adams announced in 1915 that he had discovered that the spectrum of Sirius B was similar to that of its companion.
In 1917 Adriaan Van Maanen discovered Van Maanen's star, an isolated white dwarf, which became the third to be discovered. These first three white dwarfs discovered are called classical white dwarfs., p. 2 Thereafter, many white stars were found to have high proper motion, low luminosity, and a radius similar to Earth's, so they were also classified as white dwarfs.
The peculiar name white dwarfs is due to the fact that their discoverers observed that they had a white spectrum, that is, their surface temperatures were close to 10,000 K. When the characteristics of these objects were really known, it was verified that there are several temperatures (that is, they are not all white) but that the most common were, in fact, white. In fact, they can range from very blue (temperatures above 20,000 K with maximum intensity located at wavelengths much shorter than the visible) to very red (temperatures below 000 K and maximum intensity at wavelengths long wave). However, the first to use the term was Willem Luyten, when he was examining this class of stars in 1922. The term was later popularized by Arthur Eddington.
The first white dwarfs discovered after the three classical ones were in the 1930s. In 1939, 18 white dwarfs were discovered., p. 3 Several scientists, including Luyten, continued to search for white dwarfs into the 1940s. By 1950, around 100 white dwarfs were known, and by 1999, the number was close to 2,000. Since then, the Sloan Digital Sky Survey has found 9,000 new white dwarfs.
Formation and destiny

The origin of these bodies is progressive and smooth. In mature stars the outermost layers are greatly expanded in their transformations to giant asymptotic branch stars and gradually break away from their depleted core. When the fusion reactions are finished, the nucleus contracts and heats up, although it does not reach the ignition temperature of the next phase. Before reaching that temperature, the electrons degenerate and stop the process. Thus, a white dwarf is formed with a starting temperature at its core of between 100 and 200 million degrees that will gradually cool down. The detached material will, in turn, form a planetary nebula at the center of which will be the white dwarf.
The white dwarf, once formed, gradually cools and fades, from an intense blue color to a reddish color, and then to the infrared, over time the temperature will equalize with the background radiation of the universe until, hypothetically, end up as a black dwarf, and wander in space indefinitely. To be aware of the slow cooling of white dwarfs, it should be borne in mind that the universe continues to expand, and it is estimated that in a matter of 1019 to 1020 years, the galaxies will vanish, since the stars of which they are formed will disperse through intergalactic space. Well, it is thought that white dwarfs will survive this fact, although it is true that a fortuitous collision between white dwarfs could give rise to to a star capable of producing nuclear fusion reactions (fusing helium or carbon instead of hydrogen), or to a very massive white dwarf that would give rise to a type Ia supernova. The lifetime of a white dwarf is believed to be similar to the average lifetime of the proton, which is estimated from 1032 to 1049 years according to some grand unification theories. If these theories were wrong, the proton would have to decay through complex nuclear processes, or forming virtual black holes through quantum gravity processes, and in this case the average life of the proton would be around 10200 years. If we take as true that protons disintegrate, the mass of the white dwarf would decrease very slowly due to the disintegration of its atomic nuclei, until reaching such a point that it would become a piece of non-degenerate matter, and finally it would disappear. completely.
Features
For the degenerate electrons to support the star, it must not exceed the Chandrasekhar limit, which is 1.44 solar masses. White dwarfs are known from 0.17 to 1.33 solar masses, although the vast majority of them are between 0.5 and 0.7 solar masses. The estimated radius of observed white dwarfs is between 0.008 and 0.02 times the radius of the Sun, a figure very close to the Earth's radius. (approximately 0.009 solar radii). Thus, in white dwarfs, a mass similar to that of the Sun is compressed into a volume a million times smaller, so that the density is approximately a million times greater than that of the Sun (between 106< /sup> and 107 g/cm³). They are part of compact stars, as they are one of the densest forms of matter known, only behind neutron stars, black holes, and, hypothetically, quark stars.
Since their discovery, the enormous density of these stars was already known. White dwarfs that are in a binary system, such as Sirius B or 40 Eridani B, it is possible to calculate the mass based on observations of their orbits. This was done in 1910 with Sirius B, with an approximate mass of 0.94 solar masses (more recent calculations indicate that its mass is 1.00 solar masses).
The enormous density of these stars confused astronomers who began to study them. When Ernst Öpik calculated the density of various binary stars in 1916, he estimated the density of 40 Eridani B to be 25,000 times the density of the Sun, which he called literally "impossible." As Arthur Eddington wrote in 1927:
We learn from the stars what we interpret from the light they send us. The message sent to us by Sirio's companion said: "I am composed of a material 3,000 times more dense than anything you have seen; a ton of my material would have the size of a small lingote that you could place in a box of matches." What could be answered to this message? The answer that most of us gave in 1914 was: "Shut up. Don't be silly.", p. 50Arthur Eddington
As Eddington pointed out in 1924, densities of this magnitude would imply that, according to general relativity, light from Sirius B should have a gravitational redshift. Adams confirmed this in 1925 when he was able to measure the redshift.
These densities are possible because matter is not composed of normal atoms that can form chemical bonds as we are used to, but is in a plasma state, and the nuclei and electrons are not cohesive. Therefore, in this state there is no obstacle preventing the atoms from approaching each other, otherwise it would be impossible to break into the space normally occupied by the atomic orbitals of the electrons. Eddington wondered what would happen when such a plasma cooled and the energy that keeps the atoms ionized would disappear. In 1926, R. H. Fowler resolved this paradox by applying the newly established quantum mechanics. The electrons get so close to each other that their position becomes very constrained, wanting to occupy the same quantum state, but to fulfill the Pauli exclusion principle and obey the Fermi–Dirac statistics, introduced in 1926 to determine the statistical distribution. For particles that satisfy the Pauli exclusion principle, the electrons should move very fast, pressing each other, which forms a degeneracy pressure that compensates for the gravitational one, thus stopping the collapse of the white dwarf. At absolute zero, all the electrons cannot retain the ground state, so some of them are excited to higher energy states, leaving lower energy states available, this is called a Fermi liquid. Electrons in this state are called degenerate electrons, and it means that a white dwarf can cool down to absolute zero and still contain energy. Another way to reach this conclusion is by applying the uncertainty principle: the high density of electrons in a white dwarf means that their positions are highly constrained, creating uncertainty in their dynamics. This leads to the fact that some electrons must have a large amount of movement, and therefore have a very high kinetic energy.
At these densities the ions have an extremely small mean free path; however, in the case of electrons it is the opposite: their path is exceptionally long because, being degenerate, there are very few free holes in the space of moments and positions to which an electron can go. The conductive opacity is therefore much lower than the radiative opacity. This makes transport by conduction extremely efficient inside these objects, making them almost isothermal. But this only occurs inside it, since in the atmosphere the electrons are no longer degenerate, so the gradient is considerably accentuated.
As the compression of a white dwarf increases, so does the number of electrons in a given volume of it. Applying both the Pauli exclusion principle and the uncertainty principle, we deduce that the kinetic energy of the electrons increases, which causes pressure. This electron degeneracy pressure, which enables the white dwarf to resist gravitational collapse, depends solely on density, regardless of temperature. The density is greater the heavier the white dwarf, therefore the mass is inversely proportional to the radius: the greater the mass, the smaller the radius.
The fact that the mass of a white dwarf cannot exceed a certain limit is another consequence of electron degeneracy pressure. These limits were first published in 1929 by Wilhelm Anderson and then in 1930 by Edmund C. Stoner. The current value of the limit was first published in 1931 by Subrahmanyan Chandrasekhar. Since oxygen-carbon white dwarfs are composed mainly of carbon-12 and oxygen-16, both of which have an atomic number equal to half their molecular mass, the μe must equal 2, which leads to the figure of 1.44 solar masses. Along with William Alfred Fowler, Chandrasekhar received the 1983 Nobel Prize in Physics for this work, among others. The limit is now called the Chandrasekhar limit.
This does not prevent stars with higher initial masses from ending their cycle as white dwarfs, since the intense stellar winds of the most massive stars and the final detachment of the gas cover greatly reduce the initial mass of the star to leave it within the limits of Chandrasekhar.
If a white dwarf exceeds the Chandrasekhar limit, and there are no nuclear reactions, the pressure exerted by the electrons cannot counteract the force of gravity alone, so it will collapse into an even denser object like a neutron star or a black hole. However, white dwarfs can accrete additional mass from nearby stars, which is common in binary systems. These violent contacts between a star and a white dwarf can end in thermonuclear novae and supernovae of type "Ia", in which the white dwarf would be destroyed, just before reaching the Chandrasekhar limit.
White dwarfs have very low luminosity, which is why they occupy the last band of the Hertzsprung-Russell diagram.
Relationship between radius and mass. Mass Limit
Obtaining the relationship between the radius and the mass of white dwarfs is a very simple process. The total energy of a white dwarf is obtained by adding the gravitational potential energy and the kinetic energy. The gravitational potential energy per unit mass of a white dwarf, Eg, is given by:
where G is the universal gravitational constant, M is the mass of the white dwarf, and R is its radius. The kinetic energy, Ec, increases with increasing movement of the electrons, and its equation is:
where p is the average motion quantity of electrons, m is the mass of the electron, and N is the number of electrons per mass unit. Because electrons are degenerated, we can estimate p by being depending on the amount of movement, Δpgiven by the principle of uncertainty, which states that Δp Δx is based on Planck's reduced constant. Δx is based on the average distance between electrons, whose value is approximately , that is, the reverse of the cubic root of the numerical density of electrons, n, for volume unit. Since there is a white dwarf N M electrons and their volume is based on R3, n will be given by:
Substituting into the kinetic energy equation, Ec, we get:
The white dwarf will be in equilibrium when its total energy (Eg + Ec), is minimal. At that point, the potential and kinetic energies can be compared, and a relationship between mass and radius is derived by equating their magnitudes:
Solving for the radius, R, we get:
If we eliminate N from the equation, which depends only on the composition of the star, and the universal gravitational constant, G, we obtain an equation relating the mass and the radius:
That is, the radius of a white dwarf is inversely proportional to the cube root of its mass.
This reasoning includes the formula p2/2m for kinetic energy, which is a non-relativistic formula. If we wanted to introduce relativistic calculations for when the velocities of electrons approach the speed of light, c, we would substitute p2/2 m by the relativistic approximation p c for kinetic energy. Applying this substitution:
Equating this equation to the equation for gravitational potential energy, Eg, we can eliminate R, and the mass, M, should be:
To interpret this result, we see that if we add mass to a white dwarf, its radius decreases, and according to the uncertainty principle, the momentum, and therefore the speed of the electrons, increases. As this speed increases and approaches the speed of light (c), the calculations become more accurate, which means that the mass of the white dwarf M i> is approaching Mlimit. Therefore, it is shown that no white dwarf can be heavier than the mass limit.

For a more accurate calculation of the radio-mass ratio and the limiting mass of a given white dwarf, one must calculate the equation of state that describes the relationship between the density and pressure of the dwarf's material. If we take non-relativistic calculations as an example, the radius is inversely proportional to the cube root of the mass., eq. (80) But the corrections in the relativistic calculations indicate that the radius takes the value of zero in a finite value of the mass. Said limit is the so-called Chandrasekhar limit, beyond which the white dwarf cannot withstand the force of gravity with the electron degeneracy pressure. The graph on the side shows the comparison between the relativistic calculations, represented by the green curve, and the non-relativistic ones, represented by the blue curve, on a white dwarf composed of Fermi gas in hydrostatic equilibrium. The average molecular mass per electron, μe, has been assigned a value of 2, the radius is measured in solar radii, and the mass in solar masses.
The calculations assume that the white dwarf has no rotation. If it were rotating, the hydrostatic equilibrium equation would have to be modified to include centrifugal force by taking a rotating reference frame, since for a white dwarf with uniform rotation, the mass limit increases very slightly. However, if the rotation of the star is not uniform, and viscosity is not taken into account, there would be no mass limit for a white dwarf model in static equilibrium, as Fred Hoyle pointed out in 1947. Although not all of these models of rotating stars are dynamically stable.
Radiation and Cooldown
White dwarfs emit a broad spectrum of visible radiation, ranging from the deep blue of main-sequence O-type stars to M-type red dwarfs.
The surface temperature of white dwarfs, that is, their effective temperature, ranges from 150,000 K to temperatures below 4,000 K.
According to the Stefan-Boltzmann law, greater luminosity implies greater surface temperature, so said range of temperatures on the surface corresponds to a luminosity from 100 times that of the Sun, up to one ten-thousandth of it (1/10,000). The hottest white dwarfs, whose surface temperatures exceed 30,000 K, are sources of soft X-rays (longer wavelength, closer to the ultraviolet band), that is, lower energy. This allows, through the observation of ultraviolet rays and X-rays, to obtain information about the composition and structure of the atmospheres of white dwarfs, and thus to be able to study them in depth. The radiation of a white dwarf comes from the stored thermal energy, unless it accretes mass from a companion or from any other source. Because they have such a small surface area, heat radiates very slowly, so they stay hot for a long period. As a white dwarf cools, the surface temperature drops, the spectrum of the radiation shifts toward a different color. reddish, and the luminosity decreases, and since it does not have another type of energy sink than radiation, it follows that it cools more slowly over time. For example, Bergeron, Ruiz, and Leggett estimated that a 0.59-solar-mass carbon white dwarf with a hydrogen atmosphere had cooled to a surface temperature of 7,140 K in approximately 1.5 billion years. However, they calculated that for it to cool by about 500 kelvin more (to 6,590 K), it would take 0.3 billion years, but if we repeat the process two more times (to 6,030 K and 5,550 K), it would take 0.4 and 1.1 billion years respectively. Most observed white dwarfs have a relatively high surface temperature, between 8,000 K and 40,000 K. Because they cool increasingly slowly, they spend most of their lives in cold temperatures, so when looking at the universe, we would naturally find more cool white dwarfs than hot ones. This seems to be true, but this trend stops when reaching extremely cold temperatures. Only a few white dwarfs have been observed below 4,000 K, and one of the coldest observed is WD 0346+246, with an approximate surface temperature of 3,900 K. This is explained by the fact that the age of the universe is finite, and have not had time to cool below these temperatures. A practical consequence of this is that the white dwarf luminosity function can be used to calculate the age of stars in a given region of space.
Over time, white dwarfs will cool to such an extent that they stop radiating and become black dwarfs, approaching the temperature of their surroundings and matching the microwave background radiation. However, at present, and due to the young age of the universe, there is no indication of the existence of black dwarfs.
Spectrum Classification of White Dwarfs
| Main features | |
|---|---|
| A | H lines. There are no metal lines or He I |
| B | He I lines. No metal or H lines |
| C | Continuous spectra. There are no lines |
| O | He II lines, accompanied by H or He I lines |
| Z | Metal lines. There are no lines of H or He I |
| Q | Carbon lines |
| X | Unclassifiable prospect |
| Secondary characteristics | |
| P | Magnetic white dwarf with detectable polarization |
| H | Magnetic white dwarf without detectable polarization |
| E | Emission lines |
| V | White dwarf Variable |
G. P. Kuiper was the first to attempt to classify the spectrum of white dwarfs in 1941, and various classification systems have been used ever since.
Edward M. Sion and several co-authors established the system used today in 1983, and it has been revised several times since. This system classifies the spectrum with a symbol, which usually consists of an initial D, followed by a sequence of letters shown in the adjacent table, and a temperature index, which is calculated by dividing 50,400 K by the effective temperature, since the temperature surface is closely related to the spectrum. For example:
- A white dwarf that only possesses He I absorption lines and an effective temperature of 15,000 K, will correspond, according to notation, with DB3.
- A white dwarf that possesses a polarized magnetic field, an effective temperature of 17,000 K, and a line of absorption in which the He I dominates but also has H, will be a DBAP3.
If the classification is not entirely clear, certain symbols can be used, such as "?" or ":".
Atmosphere
Although most white dwarfs are composed of oxygen and carbon, spectroscopy of the emitted light reveals that their atmosphere is composed almost entirely of either hydrogen or helium, with this dominant element being about 1000 times more abundant in the atmosphere than the others. The explanation for this fact was provided by Évry Schatzman in the 1940s, who stated that the high surface gravity separated the elements, attracting the heavy elements more strongly towards its center, leaving the lighter ones on the surface.
The atmosphere, the only part of white dwarfs that we can observe, is the upper part of a remnant of the giant asymptotic branch phase, and may contain material obtained from the interstellar medium. It has been calculated that a helium-rich atmosphere has a mass of about 1% of the total mass of the star, and an atmosphere made of hydrogen, 0.01% of the total.
Despite the fraction it represents, this outer layer determines the thermal evolution of the white dwarf; degenerate electrons conduct heat well, so the mass of the white dwarf is nearly isothermal: a surface temperature between 8,000 K and 16,000 K corresponds to a core temperature between 5,000,000 K and 20,000,000 K. The opacity a radiation from the outer layers is a measure of white dwarfs that allows them to cool more slowly.
DA-type white dwarfs, which are characterized by hydrogen-rich atmospheres, make up 80% of spectroscopically analyzed white dwarfs. The vast majority of the other types (DB, DC, DO, DZ) have atmospheres rich in helium Only a small fraction of white dwarfs, about 0.1%, have atmospheres in which the main element is carbon (type DQ). Assuming no carbon or metals, the spectral type depends exclusively on the effective temperature.. Between approximately 45,000 K and 100,000 K the most abundant spectrum would be DO, characterized by ionized helium. Between 12,000 K and 30,000 K, the helium lines would stand out, and it would be classified as DB. Below 12,000 K the spectrum is continuous and is classified as DC. It is not clear why DB white dwarfs are rare, with effective temperatures between 30,000 K and 45,000 K. One hypothesis suggests that it is due to atmospheric evolutionary processes, such as gravitational separation and convective mixing.
Magnetic field
In 1947, P. M. S. Blackett predicted that white dwarf stars should have magnetic fields of about 1 million gauss (100 teslas) on their surface, as a consequence of a physical law that he himself proposed, which stated that a body in rotation and without charge it should generate a magnetic field proportional to its angular momentum. This theory is called gravitational magnetism, also known as the Blackett effect, which has never been observed or generally accepted by the scientific community. A few years later, in the 1950s, the Blackett effect was disproved., pp. 39-43
In the 1960s, another theory was proposed that white dwarfs possess such magnetic fields because the surface magnetic flux had to be conserved during the evolution from a non-degenerate star to a white dwarf. A magnetic field on the surface of the parent star of 100 gauss (0.01 tesla) would thus become a field of 100 1002 = 1 million gauss (100 T) if the radius is reduced 100 times its size., §8;, p. 484
The first white dwarf whose magnetic field is known is GJ 742, in 1970 it was detected that the star possessed a magnetic field coming from the emission of circularly polarized light. It is calculated that the strength of the magnetic field on its surface is 300 million gauss (30 kT). Since then, magnetic fields have been discovered in more than 100 white dwarf stars, the lowest value being 2×103 gauss (0.2 T), and the highest 109 (100 kT). The magnetic field of only a small number of white dwarf stars has been calculated, and it is estimated that at least 10% of white dwarf stars have fields greater than 1 million gauss (100 T).
Crystallization

The degeneracy pressure is a quantum phenomenon independent of temperature, so white dwarfs will continue to cool throughout their lives until their temperature equals that of their surroundings, that is, until they reach almost absolute zero.
The material that makes up white dwarfs is initially plasma, but in the 1960s it was theoretically predicted that late in the cooling, the white dwarf should crystallize, starting at the center of the star.
If they get cold enough, the interactions between ions become relevant and they stop behaving like an ideal gas, becoming a Coulomb liquid. But below a certain threshold temperature (~ 1.7x107 K) the ions arrange themselves in the form of a bcc-type crystal lattice, so the white dwarf is said to have crystallized. When crystallizing, latent heat is released since it is a phase change process and this affects the luminosity function. This phase transition releases that latent energy slowing down the cooldown a bit.
The threshold temperature is calculated by means of the parameter indicated below, which is nothing more than a relation between the coulombic interactions and the thermal agitation. As long as the Coulomb energy is lower than the thermal, the behavior of the ions will be gas. When their values are comparable, it will behave like a liquid and when the Coulomb energy is clearly dominant, the star will behave as a solid, a solid of unimaginable hardness on a human scale. The crystallization threshold is normally considered to be: Γ0 ~170
Crystallization parameter:
In that equation Z is the atomic number that for a white dwarf of carbon (Z=6) and oxygen (Z=8) will be 7 assuming there is 50% of each element; K is Boltzmann's constant; T the temperature; and di is the distance between ions which is related to the density of the star by the equation (4/3)πdi³~1/ni=(μimH))/ρ, where ρ is the density, mH the mass of hydrogen, and μi the average mass number that becomes 14 for carbon and oxygen dwarfs (12+16)/2.
It happens that the oxygen crystallizes before the carbon, so in the white dwarf a nucleus of crystallized oxygen will begin to differentiate surrounded by a fluid of carbon increasingly depleted in oxygen. The emission of latent radiation will help slow down the cooling and extend the life of white dwarfs by tens of millions of years.
Another consequence of this curious phenomenon is that in crystallized white dwarfs the potential to break for the complete fusion of carbon to occur is greater, so they are potentially more explosive if they have a close companion.
In 2004, Travis Matcalfe and a team of researchers at the Harvard-Smithsonian Center for Astrophysics estimated, based on their observations, that approximately 90% of the mass of the white dwarf BPM 37093 had crystallized.
Independent studies estimate that the crystallized mass is between 32% and 82% of the total.
Pulsating White Dwarfs
| Different types of pulsating white dwarfs | |
| DAV (GCVS: ZZA) | Spectral type DA, has only hydrogen absorption lines in its spectrum. |
| DBV (GCVS: ZZB) | Spectral type DB, its spectrum has only absorption lines corresponding to the helium. |
| GW Vir (GCVS: ZZO) | Atmosphere composed of C, He and O; this group can be subdivided into: DOV and PNNV. |
Pulsating white dwarfs have the peculiarity that their luminosity is variable due to the non-radial pulsations of the gravity waves of the star itself. Observing these small variations in light emission, approximately 1% to 30%, allows data from inside white dwarfs to be analyzed using asteroseismology.
There are three large groups into which pulsating white dwarfs are divided: the first group has hydrogen-rich atmospheres and they are of the DA spectral type, they are the so-called DAV or ZZ Ceti stars. . The second group has atmospheres with abundant helium, they have the spectral type DB, and are known as DBV or V777 Her. In the last group the atmosphere is composed mostly of helium, carbon and oxygen, they are of the spectral type PG 1159, and are called GW Virginis stars. Sometimes, this last group can be subdivided into the DOV and PNNV groups of stars. Although this group cannot be considered white dwarfs proper, since they they have not reached the area of white dwarfs in the Hertzsprung-Russell diagram, and are therefore considered pre-white dwarfs.
ZZ Ceti or DAV stars
Early calculations suggested that white dwarfs would vary in periods of 10 seconds, however, in the 1960s these assumptions were rejected as they did not agree with observations.
The first ZZ Ceti found was HL Tau 76 in 1968, discovered by the American astronomer Arlo U. Landolt. Landolt observed that the star's pulsations varied over a period of approximately 12.5 minutes. In 1970, Ross 548, another ZZ Ceti with the same type of variability as HL Tau 76, was discovered. ZZ Ceti designation.
White dwarfs pulsate unstable as they traverse the effective temperature range of 10,700 to 12,500 K, which is why all ZZ Ceti fall within this range. This type of stars present brightness changes with a period between 30 seconds and 25 minutes, and an amplitude of 0.001 to 0.2 magnitudes. Fluctuations of up to almost 1 mag are sometimes observed, but this is due to the action of nearby UV Ceti companions. The measurement of the variation of the period of the pulsations in ZZ Ceti stars makes it possible to calculate the progress of the cooling of DA-type white dwarfs, and even approximations of the age of the galactic disk in which they are found can be obtained.
DBV Stars
In 1982, D. E. Winget and co-workers suggested that DB stars (white dwarfs with atmospheres composed primarily of helium) with surface temperatures near 19,000 K should emit pulses. Winget searched for stars with these characteristics, and found the variable star GD 358, a DBV, as he himself predicted it would be. This was the first prediction of a class of variable stars before its observation. In 1985, such stars were named V777 Her. These stars have effective temperatures close to 25,000 K.
GW Vir Stars
The stars GW Virginis are the third group of pulsating white dwarf variables, sometimes subdivided into the DOV and PNNV groups. PG 1159-035 is the prototype star. Variations of this star, which is also the prototype star of the PG 1159 class, were first observed in 1979, and it was designated GW Vir in 1985, giving his name to this class of stars. These stars do not literally become white dwarfs, because in the Hertzsprung-Russell diagram they occupy an intermediate position between the region of white dwarfs and the region of the giant asymptotic branch, and that is why they are called pre -white dwarfs.
These stars are very hot, their effective temperature is between 75,000 K and 200,000 K, they have atmospheres rich in helium, carbon, and oxygen, and gravity on their surface is relatively low (log g ≤ 6.5). It is possible that these stars cool to give rise to white dwarfs of spectral type DO.
Normal mode periods for GW Vir class stars range from 300 to 5,000 seconds.
The excitation of the pulsations of stars GW Vir was first studied in the 1980s, but remains a puzzle twenty years later. From the beginning, the excitation mechanism was thought to be caused by the so-called κ mechanism, associated with ionized carbon and oxygen below the surface of the photosphere, but it was thought that this mechanism would not work if there was helium on the surface. However, it appears that instability can exist even in the presence of helium.
Types of white dwarfs depending on the initial mass of the star
White dwarfs are the end of stellar evolution in main sequence stars between 0.07 and 10 solar masses. White dwarf composition differs depending on the initial mass of the star.
Low mass stars (<0.5 MSol): Helium white dwarfs.
Low-mass stars (<0.5 MSun) do not go through any phase after hydrogen combustion. Once this is exhausted, the electrons in their core degenerate long before reaching the ignition temperatures of helium, so that, at the end of their days, these stars end up becoming helium white dwarfs. Only stars of less than half a solar mass can give rise to this type of star, and a star of this mass would live for about 80 billion years. If we take into account that the age of the universe is 13 billion years, it seems logical to think that these stars have not been able to form yet. However, some objects have been found that correspond to the characteristics of helium white dwarfs. The formation of these stars can be explained by the interaction of two stars in binary systems, one star stripping the outer layer of hydrogen from a growing red star until leaving only the layer of helium, leaving the compact object bare. The phenomenon can also be explained by mass loss due to a large nearby planet.
Medium-mass stars (0.5 MSol < M < 8 MSol): Carbon-oxygen white dwarfs
If the mass of the star is between 0.5 and 8MSol, when all the hydrogen is exhausted, its core has such a temperature that it allows the fusion of helium into carbon and oxygen through the triple-alpha process. First the helium in the core is consumed, and once exhausted, the available helium in a layer around it begins to be consumed. This causes the star to expand for the last time: the phase of the giant asymptotic branch begins. As the amount of carbon resulting from triple alpha reactions increases, the chances of forming oxygen also increase, but the ratio of carbon to oxygen is unknown since their cross sections are not well defined. Arriving at the final moments of the star, it will intensify its stellar winds more and more, progressively expelling its hydrogen cover until leaving a bare and degenerate core of carbon and oxygen. A star like the Sun will expel 40% of its mass in its final spasms before ending its days as a white dwarf. The nebula resulting from the expulsion of the outer layers is called a planetary nebula.
Remnants of stars with masses between 1.5 and 9 solar masses could well exceed the mass of Chandrasekhar. If they all evolved to explode as supernovae, as would be expected, many more would be observed in the sky. Furthermore, the metal composition of interstellar gas should be richer in iron than in oxygen, which is not the case. This is explained by the large amount of mass ejected by the strong winds of these stars, reaching losses of 8 solar masses throughout their lives. These mass losses will be all the more accentuated the larger the star, as well as the greater its metallicity, which increases the opacity. Therefore, stars in this mass range also end their lives as carbon-oxygen white dwarfs. These types of white dwarfs are the most common observed in the universe.
The boundary between medium-mass and high-mass stars (8 MSol < M < 10 MSol): Oxygen and neon white dwarfs?
High-mass stars reach the temperature in their cores necessary to fuse carbon into neon, and then neon into iron. Their final destination is not a white dwarf, since they exceed the maximum allowed mass and the electron degeneracy pressure cannot cope with gravity, so the core collapses and the star explodes in a type II supernova, leaving as a remnant a neutron star, black hole, or exotic form of compact star. However, some stars between 8 and 10 MSol may be able to fuse carbon to produce neon, but not be massive enough to burn neon. If this happens, the core does not collapse, and the merger does not become too violent, it would give rise to a white dwarf composed of oxygen, neon, and magnesium. These stars come from the so-called ONeMg or neon novae, whose spectrum shows high abundances of neon and magnesium. The problem in determining the range of masses that give rise to these objects stems from the high rates of mass loss at the end of the lives of stars, which makes it difficult to accurately simulate numerically which stars stop at carbon, which in oxygen-neon and which reach iron. Thus, the exact value may depend on the metallicity of the star.
Type Ia Supernovae: Iron-Cored Dwarfs?
Type Ia supernovae have also been proposed as another way to form (rather, transform) white dwarfs. In this scenario, the explosion that occurs in this type of supernova is not powerful enough to completely destroy the white dwarf and is limited to expelling part of its matter at high speeds as well as, being asymmetric, catapulting the dwarf. white at high speeds making it a hypervelocity star. The matter that has been processed in the failed supernova is recaptured by the white dwarf, with the denser elements such as iron falling to the center of the star and accumulating there.
These iron-core white dwarfs would be smaller than their carbon-oxygen counterparts and would crystallize and cool faster as well.
Interactions with the star system
The stellar or planetary system of a white dwarf star can play a role in its development in several ways. NASA's Spitzer Space Telescope observed the central area of the Helix Nebula using infrared spectroscopy, and suggested that a cloud of dust was located there, probably caused by collisions between comets. presence of a dust cloud around the white dwarf G29-38, possibly formed by the tidal breakup of a comet that transited very close to the white dwarf.
There have also been authors who have suggested that white dwarfs could be accompanied by the remains of terrestrial-type planets, which would have survived the red giant phase but losing their outer layers and only remaining their core; further studies The abundance of metals in the atmospheres of white dwarfs reinforce this idea and suggest that at least 15% of these objects may have planets and/or asteroids orbiting them, or at least the aforementioned remains of such bodies, which also implies that at least 3.5% of stars in spectrum A and F may have planetary systems.
If a white dwarf is in a binary system with a companion, several phenomena can occur:
Type Ia Supernova
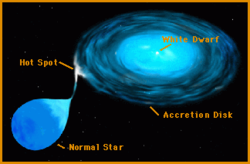
The mass of an isolated, non-rotating white dwarf cannot exceed the Chandrasekhar limit of 1.4 solar masses, although this limit increases slightly if the white dwarf rotates rapidly on its axis. are part of binary systems can accrete material from their partner, usually a red giant, thus increasing both in mass and density. Once the mass has reached the Chandrasekhar limit, the electrons are no longer able to support the star, which increases the pressure, which shoots up the temperature until fusion starts in the dwarf's core that produces an explosive ignition, or collapses to form a neutron star. According to the most common model for the formation of type Ia supernovae, a carbon-oxygen white dwarf accretes material from a companion, thereby increasing its mass and compacting its core. The heat of the core allows carbon reignition to start when the mass exceeds the Chandrasekhar limit. White dwarfs, since they counteract gravity by using degeneracy pressure instead of thermal pressure, adding heat increases the temperature but not the pressure, so the white dwarf is not expanding. Instead, the temperature accelerates the rate of fusion of the star. The thermonuclear flame consumes a large part of the white dwarf's carbon in a few seconds, causing a type Ia supernova explosion that ends up destroying the star and ejecting its mass at speeds close to 10,000 km/s, dissipating large amounts of dust and gas. But this is not the only valid mechanism for the formation of type Ia supernovae, if two white dwarfs made of carbon and oxygen that make up a binary system collide and merge, forming a body with a mass greater than the limit of Chandrasekhar, the carbon can ignite, causing the explosion., p. 14.
Cataclysmic Variable Stars
When, despite the accretion of material, the mass does not reach the Chandrasekhar limit, the accreted hydrogen on the surface can ignite leading to a thermonuclear explosion. Since the core of the white dwarf does not suffer the effects of these explosions, the dwarf can continue to accrete hydrogen and continue to explode. This cataclysmic phenomenon is called a nova. Dwarf novae have also been observed, which have weaker luminosity peaks than the novae themselves. These phenomena are not produced by nuclear fusion, but are due to the gravitational potential energy that occurs during the accretion of material. In general, a cataclysmic variable star refers to any binary system in which a white dwarf accretes matter from a companion. Apart from novae and dwarf novae, many different classes of variable stars are known. Cataclysmic variable stars, both by accretion and merger, have been shown to be sources of X-rays.
Possible habitability
In 2011 it was suggested that white dwarfs with surface temperatures below 10,000 Kelvin could have a habitable zone that would extend between 0.005 and 0.02 astronomical units and whose duration would be 3000 million years, proposing to search around white dwarfs terrestrial-type planets that could orbit there either after migrating from outer orbits, or forming there; because white dwarfs are similar in size to such bodies, transits such hypothetical planets could produce would produce major eclipses; later studies, however, propose that a planet orbiting a white dwarf at such a close distance would be subject, among other effects, to tidal forces caused by its star, which could produce an intense greenhouse effect in it, making it uninhabitable and making it more difficult for them to be habitable. Another problem with this theory is that, apart from the fact that a planet could form on a accretion disk around a white dwarf, to reach such a tight orbit it could only achieve it in two ways: being absorbed by its star during the red giant phase and surviving its spiral fall towards the stellar core (very difficult for bodies of low mass), or being sent to it after gravitational interactions with other bodies (in which case such quantity would be released orbital energy into heat that it is quite possible that the planet would eventually become an uninhabitable ember)
Contenido relacionado
(11) Parthenope
Conductance
Galileo (disambiguation)