Wheatstone bridge

ImprimirCitar

Un Puente de Wheatstone tiene cuatro resistencias que forman los lados de un rombo. Se alimenta con una fuente de voltaje continua en sus extremos y en el centro se conecta un galvanómetro.

Wheatstone Bridge layout..

A Wheatstone bridge is an electrical circuit used to measure unknown resistances by balancing the arms of the bridge. These are made up of four resistors that form a closed circuit, one of them being the resistance under measure.

The English physicist and inventor Charles Wheatstone (1802-1875) is best known for being the first to apply the electrical circuit that bears his name (Wheatstone bridge) to measure resistance. It had actually been previously designed by Samuel Hunter Christie in 1832, so Wheatstone's role was to improve and popularize it, beginning in 1843.

Description

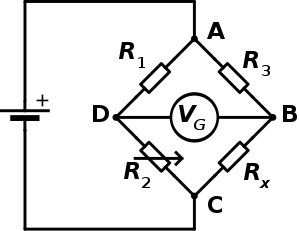
In the diagram on the right we have R_x, which is the resistance whose value we want to determine; R₁, R₂ and R₃ are resistors of known values, and resistor R₂ is adjustable for set the balance point. If the ratio of the two resistances of the known arm (R₁/R₂) is equal to the ratio of the two of the unknown arm (R₃/R_x), the voltage between points D and B will be zero and no current will flow through the galvanometer V _G. In case of imbalance, the direction of the current in the galvanometer indicates whether R₂ is too high or too low. The voltage value of the power supply (Vs) is irrelevant and does not affect the measurement.

To carry out the measurement, the resistance R₂ is varied until reaching the equilibrium point. Zero current detection can be done with high precision using the V_G galvanometer.

In equilibrium condition it is always fulfilled that:

${displaystyle {begin{aligned}{frac {R_{2}}{R_{1}}}&={frac {R_{X}}{R_{3}}}\[4pt]Rightarrow R_{X}&={frac {R_{2}}{R_{1}}}cdot R_{3}end{aligned}}}$

When the bridge is built such that R₃ equals R₁, R_x equals R₂ in equilibrium condition (zero current through the galvanometer).

If the values of R₁, R₂, and R₃ are known very precisely, the value of R_x can be equally precisely determined. Small changes in the value of R_x will break the equilibrium and will be clearly detected by the galvanometer indication.

Alternatively, if the values of R₁, R₂ and R₃ are known and R₂ is not adjustable, the current through the galvanometer can be used to calculate the value of R_x, this procedure being faster than zeroing the current through the meter.

Demo

Current directions are arbitrarily defined

First we use Kirchhoff's current law (KCL) to find the current flowing in nodes D and B (I_G):

Node D:

{displaystyle {begin{aligned}I_{1}-I_{2}-I_{G}&=0end{aligned}}}

Node B:

{displaystyle {begin{aligned}I_{3}-I_{X}+I_{G}&=0end{aligned}}}

Then we use Kirchhoff's voltage law (KVL) to find the voltages of the meshes ABD and BCD:

ABD Mesh:

{displaystyle {begin{aligned}V_{3}-V_{G}-V_{1}&=0\Rightarrow (I_{3}cdot R_{3})-(I_{G}cdot R_{G})-(I_{1}cdot R_{1})&=0\end{aligned}}}

BCD Mesh:

{displaystyle {begin{aligned}V_{X}-V_{2}-V_{G}&=0\Rightarrow (I_{X}cdot R_{X})-(I_{2}cdot R_{2})-(I_{G}cdot R_{G})&=0end{aligned}}}

When the bridge is balanced, then $I G = 0$ , then the second set of equations can be rewritten as:

{displaystyle {begin{aligned}I_{3}cdot R_{3}&=I_{1}cdot R_{1}\I_{X}cdot R_{X}&=I_{2}cdot R_{2}end{aligned}}}

So, dividing the equations and rearranging, you get:

{displaystyle {I_{3} over {I_{1}}}={{R_{1}} over {R_{3}}}}

{displaystyle {I_{X} over {I_{2}}}={{R_{2}} over {R_{X}}}}

Again, if $I G = 0$ , then $I 3 = I X$ and $I 1 = I 2$ .

such that:

${displaystyle {I_{3} over {I_{1}}}={{I_{X}} over {I_{2}}}}$

then:

${displaystyle {R_{2} over {R_{X}}}={{R_{1}} over {R_{3}}}}$

Clearing, we obtain that the desired value of $R X$ to achieve equilibrium is:

{displaystyle R_{X}={{R_{3}cdot R_{2}} over {R_{1}}}}

If we know the values of the four resistors and the power supply ( $V S$ ), and the resistance of the galvanometer is high enough so that $I G$ is negligible, the voltage across the galvanometer ( $V G$ ) can be determined by working with the voltage of each voltage divider by subtracting them from each other. The resulting equation is:

{displaystyle V_{G}=left({R_{2} over {R_{1}+R_{2}}}-{R_{X} over {R_{X}+R_{3}}}right)V_{S}=0,{text{ al sustituir }}R_{X}}

where $V G$ is the voltage between nodes D and B.

Typical Wheatstone Bridge

Variants

Variants of the Wheatstone bridge can be used for the measurement of impedances, capacitances and inductances.

The bridge arrangement is also widely used in electronic instrumentation. To do this, one or more resistances are replaced by sensors, which, when their resistance varies, give rise to an output proportional to the variation. At the exit of the bridge, where the galvanometer is, ( $V G$ ) is usually placed an amplifier.

Kelvin Bridge

The Wheatstone bridge is the fundamental, but there are other variants that can be used to measure different types of resistances when the fundamental Wheatstone bridge is not adequate. Some of those variants are:

Carey Foster Bridge, to measure small resistances.
Kelvin Bridge, to measure small resistances of four terminals.
Maxwell Bridge, to measure impedances.
Hay Bridge for inductance measurement.
Bridge of Wien

Electronic scale

The Wheatstone bridge is widely used in electronic balances based on Strain Gauge, the objective of these devices is to measure an output voltage proportional to the variation of the weight supported on it.

Contenido relacionado

Más resultados...

Wheatstone bridge

Description

Demo

Variants

Electronic scale

Contenido relacionado

Irene Joliot-Curie

Potentiometry

Trans siberian