Wavelength

Wave length in a sinusoid represented by the Greek letter λ (lambda).

In physics, the wavelength is the distance covered by a periodic disturbance that propagates through a medium in one cycle. The wavelength, also known as the spatial period is the inverse of the frequency multiplied by the speed of propagation of the wave in the medium through which it propagates. Wavelength is often represented by the Greek letter λ.

Generally, the concept of wavelength is associated with sinusoidal waves, although it can be extended to any periodic wave. The magnitude of the wavelength can be determined as the distance between two consecutive maxima of the disturbance. For example, in an electromagnetic wave, the wavelength corresponds to the distance between two electric field maxima. In the case of ocean waves, the wavelength coincides with the separation between two consecutive crests.

Wavelength is measured in multiples or submultiples of the meter in units of the International System of Units. The wavelength of visible light is on the order of nanometers. Radio waves have a wavelength between centimeters, meters and even kilometers. The wavelengths of sounds audible to humans are between about 17 meters —for low sounds— and 17 millimeters —high sounds—. The wavelength depends on the medium in which the disturbance propagates. In non-uniform media, the wavelength can vary with position. Some complex waves can be expressed as the superposition of simple sine waves; the range of wavelengths that the wave comprises is called the spectrum.

Sine Waves

Fourier series applied to approximate a square wave as a sum of one, two, three and four spectral components.

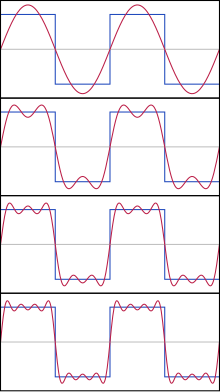
By Fourier's theorem, any periodic wave can be expressed as the weighted sum of sinusoidal waves of different wavelengths. In other words, any periodic wave, regardless of its shape, can be decomposed into a series of sine waves. This property makes it possible to study the behavior of a multitude of waves by analyzing each of its components, called spectral components.

In a sinusoidal wave of frequency f and period T, the wavelength is given by the expression:

λ λ =uf=u⋅ ⋅ T{displaystyle lambda ={frac {u}{f}}=ucdot T}

Symbol	Name
λ λ {displaystyle lambda }	Wave length
f{displaystyle f}	Frequency
T{displaystyle T}	Period
u{displaystyle u}	Speed of wave propagation

In the case of electromagnetic waves propagating in a vacuum, the speed of propagation is the speed of light; in the case of sound waves, it is the speed of sound. In media known as non-dispersive this speed of propagation is the same for any wavelength.

Standing Waves

Stationary wave (in black) represented as the sum of two waves spreading in opposite senses (in red and blue).

A standing wave consists of a wave motion that does not propagate, but remains confined in space. In standing sinusoidal waves there are points, called nodes, that remain stationary. The distance between two nodes is half the wavelength.

Three stationary waves confined.

As a result of border conditions, stationary waves must have nodes at the limits of the space where they exist, which restricts the value of wavelengths allowed to those that meet the relationship λ λ n=2Ln{displaystyle lambda _{n}={frac {2L}{n}}}}Where L{displaystyle L} is the length of the medium and n{displaystyle n} It's any whole number.

A standing wave can be represented as the superposition of two waves propagating in opposite directions. As a consequence, the wavelength, frequency, and speed of the standing wave bear the same relationship as for a normal wave.

Media dependency

Separation of wavelengths by a prism.

Waves propagate at constant speed and in a straight line in homogeneous media. However, when the wave encounters a material with different characteristics, part of the wave is transmitted to the second medium, while another part is reflected. The reflected wave propagates in the opposite direction to the incident wave and maintains the wavelength, but the wave that penetrates a different medium undergoes a change in speed and direction (refraction).

The speed of propagation decreases with the density of the medium, so when the wave is transmitted to a denser material the wavelength decreases and vice versa. In general, the relationship between the wavelengths in the two media is:

λ λ 1λ λ 2=n2n1{displaystyle {frac {lambda _{1}}{lambda _{2}}=}{frac {n_{2}}{n_{1}}}}}}}}}}

where n1{displaystyle n_{1} and n2{displaystyle n_{2}} are the respective refractive rates.

The change in direction of the incident wave is dictated by Snell's law. Yeah. α α 1{displaystyle alpha _{1}} and α α 2{displaystyle alpha _{2}} are the angles of incidence and refraction of electromagnetic wave the relation is fulfilled:

n1sen α α 1=n2sen α α 2{displaystyle n_{1}operatorname {sen} alpha _{1}=n_{2}operatorname {sen} alpha _{2}}}}

Snell's law implies that the direction of propagation of refracted light depends on the wavelength. Therefore, when a beam of visible white light falls on a surface of a different material, the beam is separated into all the wavelengths that make up its spectrum, forming a rainbow. This effect is known as scattering.

Non-uniform media

A wave that spreads in an inhomogeneous medium. As the wave loses speed the wavelength decreases and the amplitude increases to a maximum after it fades.

Waves with temporal periodicity that propagate in an inhomogeneous medium, whose properties change with position, can propagate with a speed that depends on position, so they lose spatial periodicity. For example, waves in a body of water that approach the shore have a wavelength that varies with the depth of the water and the height of the wave compared to its wavelength.

The analysis of the equations that govern these systems is frequently carried out by the WKB approximation or the Liouville-Green method, consisting of integrating the phase of the wave over all space using a local wave number; this method is equivalent to treating the system as locally uniform; the wavelength at a given point can be calculated from the local speed of the wave and its frequency.

Crystal waves

A wave caused by vibrations of atoms arranged at regular distances can be described by different wavelengths.

Waves in crystalline solids are not continuous, because they are made up of vibrations of particles arranged in a regular lattice. This results in overlap as the wave can be described in terms of different wavelengths. By convention, the longest wavelength that fits the wave is used. The wavelength spectrum that describes all possible waves in a crystalline medium corresponds to the wave vectors confined to the Brillouin zone. This indeterminacy of the wavelength in solids is important in the analysis of phenomena such as energy bands, and network vibrations.

Wavelength associated with particles

Louis-Victor de Broglie postulated that all particles that possessed a momentum were associated with a certain wavelength. It is the so-called De Broglie Hypothesis, the basis of quantum mechanics.

λ λ =hp{displaystyle lambda ={frac {h}{p}}}}

Symbol	Name
λ λ {displaystyle lambda }	Wave length associated with particles
h{displaystyle h}	Constant of Planck
p{displaystyle p}	Number of motion of particle

This wavelength associated with a particle is known as the De Broglie wavelength. The de Broglie wavelength of an electron in a cathode tube is about 10⁻¹³ m. Wave packets are used to represent subatomic particles located at a point in space. The length of the wave packet and the extent of the wave numbers of the waves that make up the packet correspond to the uncertainty of the position and momentum of the particle respectively, whose product is given by the Heisenberg uncertainty principle.

Wavelength multiplexing

Electromagnetic waves (such as light) have a certain wavelength in relation to their frequency. For example, the wavelength of red light is around 645-700 nm; frequencies lower—and therefore longer wavelengths—than red are called infrared and are not visible by the human eye.

It is possible to transmit information through a certain wavelength and mix it with other similar transmissions in the same medium, differentiating all of them through their original wavelength. In fact, it is what we do when tuning a radio device: we choose one of the many emissions that exist in the electromagnetic spectrum. This principle is used in optical fibers where various pieces of information are transmitted over the same fiber in a process called wavelength multiplexing, which can be "dense" or "thick" depending on the number of channels and the precision required for the multiplexing, and of course the cost of implementation. This is widely used in submarine fiber optic cables, an evolution of the frequency division multiplexing systems previously used in coaxial cables.

Wavelength converter

A wavelength converter is a device that is responsible for converting the wavelength of the data carrier into a different carrier, that is, changing the frequency of the input signal into a different and desired one at the exit. In the field of telecommunications, it is very useful since it allows the connection between uncoordinated optical networks and also makes it possible to make the most of the available optical frequencies in an efficient manner.

Depending on the type of converter, the device consists of one or two input signals. These signals will always be optical given the purpose of the device. However, it will always consist of an output signal, also optical. There are different types of wavelength converters:

• Optoelectronic wavelength converter: This converter consists in its first stage of an optoelectric receiver that transforms the λ signal_in of entry into an electrical signal. This electrical signal is used in the electron transmitter as a source to create a copy of the input signal to a different and desired wavelength, λ_conv.
• All-optical wavelength converter (all-optical): This converter is based on non-linear optical effects to transfer the input signal modulation λ₁ (data signal to which you want to change the wavelength) to an unmodulated continuous signal, λ₂. Therefore, at the output you have the information of the data input signal to the wavelength of the continuous signal. This type of converter can be subdivided according to its main operating methods in two categories: consistent wavelength converters and cross modulation wavelength converters. Last Cross Modulation Wavelength Converter, it is again subdivided into four other categories depending on the properties of the nonlinear optical medium and the modulation of the optical signal: modulation of cross profit (XGM, cross-gain modulation), cross-phase modulation (XPM, cross-phase modulation), cross absorption modulation (XAM, cross-absorption modulation) and differential polarization modulation (DPM, differential polarization modulation).

One of the big differences between the two converters is the speed they can achieve. In the case of optoelectronic converters, rates of 2.5 Gbps can be reached, due to the limitations imposed by the electronic components, while in the case of all-optics, up to 40 Gbps can be reached. Another disadvantage of these (optoelectronic) converters is that they are not transparent to the modulation of the input signal. This is because they are not capable of processing different modulations and therefore the information contained in the intensity, frequency, phase or polarization of the signal must be reprocessed for wavelength conversion or it will be lost.