Wave Propagation

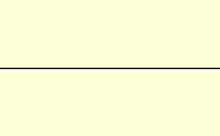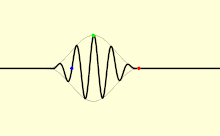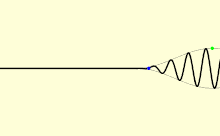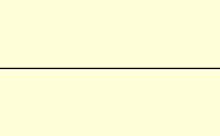
The propagation of a wave can be interpreted using the linear chain model. This chain is composed of a series of particles of equal mass separated from equally equal springs. This model allows us to explain the behavior of elastic bodies and therefore the propagation of mechanical waves.

In the case of sound and light waves, it is customary to analyze a wave as the sum of simple sine waves. This is the principle of linear superposition. In contrast, when one carefully observes waves on the surface of water, one sees that this principle cannot be applied in general to their description, except when small amplitudes occur. The study of small amplitude waves in water was one of the main topics of physics in the 19th century. During the middle of the 20th century, the study of many non-linear phenomena gained special importance; For example, laser beams in nonlinear optics and waves in gases in plasmas exhibit nonlinear phenomena.

The importance of such phenomena has led to more careful studies, which has revealed that the propagation of nonlinear waves is considered fundamental entities in wave waves. Stable waves in a nonlinear and dispersive response medium are known as solitons.

The above problem motivated Enrico Fermi, John Pasta and Stanislam Ulam (FPU) to carry out numerical experiments in chains of oscillators with non-harmonic interaction potentials in the early 1950s. They thought that if the energy was placed in the lowest oscillation mode (longest wavelength mode), the equipotentialization of the energy would eventually take place. The relaxation time for this to occur would provide a measure of the diffusion coefficient. To the surprise of Fermi and his colleagues, the energy of the system was not 'thermalized'. Only a fraction of the energy was distributed among the other modes and, in a later, long but finite time, almost the same amount of energy was re-concentrated in the lowest mode. This is known in mechanics as a recurrence phenomenon, similar to that observed in the movement of two coupled pendulums, in which the oscillation energy remains in one mode for a certain time and then passes to another. It turns out that the recurrence time for a sufficiently large number of coupled oscillators exceeds any physical observation time

The explanation for this discovery remained a mystery until Norman Zabusky and Martin Kruskal began studying this system again in the early 1960s. the lowest order modes (long wavelength), led them to propose a continuous approximation of the system and study the partial differential equation called KdV.

This equation had been obtained in 1885 by D.J. Korteweg and Gustav de Vries in the description of the propagation of long wavelength waves in shallow waters.