Vigesimal system

The vigesimal system is one of the positional numeral systems for naming, writing and counting numbers, whose base is the number twenty. The decimal number system and the vigesimal number system are the systems most frequently used in the world's languages for counting. Celtic languages, Euskera or Mesoamerican languages used counting systems based on the vigesimal system.

The representation of numbers

In the same way that in the decimal system the base is the number 10, in the vigesimal system the base is the number 20. In the vigesimal system 20 units of lower order are equivalent to one unit of immediate higher order. The numbers are counted by twenty. It is speculated that this system would have had its origin in the number of all the fingers and toes of a human being.

In the decimal system we count units (from one to nine), tens (10 X 1 = 10, 10 X 2 = 20, 10 X 3 = 30...), hundreds (100 X 1 = 100, 100 X 2 = 200, 100 X 3 = 300..), thousands (1000 X 1 = 1000, 1000 X 2 = 2000...), ten thousands (10000 X 1 = 10000, 10000 X 2 = 20000...), hundreds of thousands (100000 X 1 = 100000, 100000 X 2 = 200000...), millions... etc. Ten units make a ten. Ten tens make a hundred and so on.

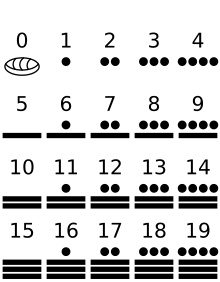
In the vigesimal system, the class of simple units contains a set of twenty elements. And when counting by having 20 units, it is assumed that they form the class of twenty, the class of second order. Twenty scores make up the third-order class. And then there are different series that are counted by twenty. That means that the first count goes from the number zero to nineteen.

When typing 835_v, 5 indicates 5 hats; 3 shows 3 boxes of 20 hats each; 8 indicates 8 warehouses each with 20 boxes, in total 160 boxes = 3200 hats.

Twenties are counted from number one to 19, starting with the first twenty up to the 19th twenty.

The following series is based on the number 400 (400 X 1 = 400, 400 X 2 = 800...). The series based on the number 400 is computed with the help of the nineteen units.

The following series is based on the number 8000 (8000 X 1 = 8000, 8000 X 2 = 16000, 8000 X 3 = 24000...).

So the decimal number two thousand and eleven (2011) in the vigesimal system is 05.00.11. That is, 5 series of four hundred, zero series of twenty, 11 units.

2011 = (5 X 400) + (0 X 20) + 11 units.

The representation through glyphs

The representation of numbers can be through glyphs. The ancient Mexicans used a flag to represent the scores and a feather to represent the series based on the number 400; a sack to represent the series based on the number 8000.

20 →

400 →

8000 →

It can happen that a glyph is repeated several times, in a way analogous to the repetition of dots to indicate a plurality of units.

60 →

Representation by numbers

The numerical representation has variants:

A) The western representation (which is not typical of the American peoples, because they did not use Arabic numerals or use points to separate the series).

In the first variant we use dots to separate the different series. Each series has two digits to account for the 19 units that fit in each series:

00.00.00.00.00.00.00

So 112 million would be 01.15.00.00.00.00.00, a number that represents a series of 64 million, 15 series of 3,200,000, zero series of 160,000, zero series of 8,000, zero series of 400, zero series of 20 and zero units.

B) The Mexican representation (Mayas, Nahuas).

The Mayas and Nahuas did not separate the series by points. The separation of the series was achieved by writing vertically, from top to bottom. The units occupied the bottom place. One line above was the series based on the number 20. One line above the series based on the number 400... etc.

Thus, the figure 112 million was represented as follows.

Mayan numeration.

01

15

00

00

00

00

00

And they did not use Arabic numerals but their own system of dots and dashes, in which each dot represented one unit and each dash five units. The number zero (ahtle) was represented by a shell.

Representation through words

In the same way that in Spanish we have words that designate decimal quantities, the speakers who used the vigesimal system used their own terminology. Most Indo-European languages use a decimal number system, which means that number names are grouped in series of ten, and that there are roots for the numbers one through nine, ten, one hundred, one thousand, and the other names are derived from the roots for the cited numerals. Other families of languages also use the decimal system and there are families of languages where vigesimal systems are used (Basque, Mayan languages, Utoaztec languages, etc.). Some languages have base five subsystems, within a decimal or vigesimal system.

Speakers of the Nahuatl language used the word pohualli for the series based on the number 'twenty':

Cempohualli (20), ompohualli (40), epohualli (60), nauhpohualli (80), macuilpohualli (100)...

In the above forms ce(m) is '1', om(e)-/on- is '2&# 39;, e(i)- is '3', nahui > nauh- is '4& #39; etc

They used the word tzontli for the series based on the number four hundred:

Centzontli (400), ontzontli (800) etzontli (1200)...

The word xiquipilli was chosen for the series based on the number 8000:

Cenxiquipilli (8000), onxiquipilli (16000), exiquipilli (24000)...

Other words were poalxiquipilli (8,000 X 20 = 160,000), tzonxiquipilli (160,000 X 20 = 3,200,000), poaltzonxiquipilli (3,200,000 X 20 = 64,000,000)...

When saying a number orally, they inserted the preposition «ipan» (on) between the different series, because that was how they represented it, the larger series on the smaller ones.

If they wanted to multiply 4 ones by 2 ones, they would say "nappa ome" (four times two).

If you wanted to divide 4 units by 2, "nahui itzalan ome" (four by two).

If they wanted to add 4 plus 2, they would say "nahui ihuan ome" (four plus two).

If they wanted to subtract 4 minus 2, they would say "nahui iyoh ome" (four minus two).

If they wanted to say 4 comma two, they would say "nahui ica ome" (four with two).

The = sign was called "inamic", which means equal to, equivalent to.

16 + 42 = 58 → caxtolli once ihuan ompohualli omome inamic ompohualli ipan caxtolli omeyi.

The decimal series of the vigesimal system have their own name in Spanish: twentyths, tetrahundredths and eightthousandths. Below will be his name in Nahuatl.

The decimal quotient expressed vigesimally and the vigesimal quotient expressed decimally

Decimal quotient or decimal is a non-integer number and represents a fraction or part of an integer, but not of any integer but of unity. Decimals exist in the decimal system and in other number systems, such as the vigesimal system.

0.25 (twenty-five hundredths)

0.05 (five hundredths)

0.5 (five tenths)

1,000,000.5 (one million units with a decimal ratio of five tenths)

In non-technical language, we often express these quantities in loose language. For example:

0.12 (zero comma twelve)

But this non-technical language does not help us to indicate if we are in a decimal system or in another system.

Decimal numbers are subdivided into decimal units and decimal quotient.

The logic of the concept of the decimal quotient is so characteristic that if in the vigesimal system we want to write 23,23 (= 01.03,04.12) we observe that we cannot write it as 01.03,01.03.

Similarly, if we write a zero to the right of a decimal unit, the quantity increases.

10 (units) → 100 (units)

But if we write a zero to the right of a decimal quotient, the amount doesn't increase but only changes the paradigm.

0.1 (one tenth) = 0.10 (ten hundredths) → the amount is the same but otherwise expressed — with another model or paradigm.

This justifies dedicating a specific section to the decimal quotient within decimal numbers.

In the vigesimal system, tenths, hundredths or thousandths are not expressed as decimals, but there are decimals. The tenths, hundredths and thousandths are expressed vigesimally. Because when a mathematician says in the decimal system that 0.5 is five tenths, or fifty hundredths, or five hundred thousandths... he is referring to a value that represents half of the unit and the same thing happens when a mathematician in the decimal system vigesimal says that 00.10 is half a unit. Both mathematicians are expressing the same idea.

* 0.5 (five tenths expressed decimally) = 00.10 (five tenths expressed vigesimally).

* 0.06 (six hundredths in the decimal system) = 00,01.04 (six hundredths expressed vigesimally).

* 3.23 (3 units with 23 hundredth expressed decimally) = 03.04.12 (3 units, with 23 hundredth expressed vigesimally).

A Native American will say that Europeans express twentyths as decimals and a Native European that Americans express tenths as vigesimally:

00,04.12—for an American native "four twentieths, twelve tetracentesimas" or "four over twelve tetracentesimas", an expression proper to the vigesimal system—a European native is ninety-two tetracentesimas (4 X 20 + 12 = 92), an expression proper to the decimal system that constitutes another paradigm of the decimal quotient.

The numerical representation in the calendar

Just as Westerners use the decimal system, the Mayans and Nahuas used the vigesimal system. But, like Westerners, the account had modifications to the calendar account.

The Mayans had 20 days (which they called kines). With 20 kines they made a uinal and with 18 uinals they made a tun (of 360 kins) —instead of twenty uinals—

The week of the Nahuas was 5 days long and the month was divided into four weeks of 5 days.

There was another bead, that of the “tonalamatl”. According to which, for example, Tenochtitlan falls into the hands of the Spanish on the day (tonalli) “ce coatl” (one snake), of the month (metztli) “tlaxochimaco », from the year (xihuitl) «yei calli» (three houses) which corresponds to August 13, 1521.

Numeric operations in the vigesimal system

Sum in the vigesimal system

1) An example with figures written vertically.

To add 25 (1.05) plus 25 (1.05), whose result is 50 (2.10), the procedure is simple.

01 + 01 = 02 (two sets of twenty)

05 + 05 = 10 (ten units)

2) An example with figures written horizontally.

In this case we are going to add 75 + 75 = 150.

In the vigesimal system:

03.15 (suming)

+03.15 (suming)

-...

07.10 (total)

Procedure used to find the total:

First add the units (15 + 15 = 30). Since 30 is greater than 20 by 10, we put 10 ones down in the total. And we pass the remaining 20 to the next series, that is, to the series of 20.

In the series of 20 we add 03 + 03 = 06. And we add one more unit that we had from the previous series. 06 + 01 = 07.

Check: (7 X 20) + 10 = 140 + 10 = 150.

Read and write order. Order to Operate

As in the decimal system, in the vigesimal system it is read starting with the series with the highest value and ending with the units. That means that it is read from left to right —and in his case, if the writing is vertical, from top to bottom.

If we want to write a number, we respect that same order.

But we don't respect it if we're operating. In the decimal system, we operate from right to left. That is, first the units are added and then the series with the highest value (tens, hundreds, thousands). This happens to be able to count the carried ones.

Subtraction in the vigesimal system

Let's subtract 150 - 75 = 75.

07.10 (minute)

-03.15 (sustrating)

-...

03.15 (review)

We start with the units. To the 10 units of the minuendo we add 20 units, because the 10 units of the minuendo are less than the 15 units of the subtrahend. 30 - 15 = 15. We write down 15 units on the remainder.

As in the minuendo we have added 20 units to 10 to obtain 30, now we take 20 units, which go on to the next series of 20 of the subtrahend (03 + 01 = 04).

And finally we subtract the series of 20 (07 -04 = 03) and write down the result in the remainder.

Another example 180- 65 = 115.

09.00 (minute)

-03.05 (sustrating)

-...

05.15 (rest)

To the units of the minuendo we add 20, we subtract 05 and it gives us 15 (which we write down in the rest).

And we add 03 + 01 = 04 in the subtrahend and subtract 09 -04 = 05 (which we write down in the remainder).

Peculiarity of the carry in the vigesimal system

Let's go back to the previous example. Let's subtract 150 - 75 = 75.

07.10 (minute)

-03.15 (sustrating)

-...

03.15 (review)

As the units of the minuend are ten and those of the subtrahend are fifteen, in the minuend we are forced to decompose twenty units. That is to say, we subtract twenty from the units: twenty plus ten make thirty.

And so we add a score to the score of the subtrahend.

The procedure is the same as in the decimal system, but with the peculiarity that in one case the series are twenty and in the other ten.

Congruence of the minuend with the subtrahend

To find the result of 00.10 minus 00.01.08, we are forced to put some trailing zeros in the minuend:

00.10.00 (low)

- 00.01.08.

----------------

00.08.12 (return)

This occurs because we have to operate with equivalent units.

Multiplication in the vigesimal system

First we will put a simple example with vertical numbers:

To multiply 25 (01.05) by four (04), whose result is 100 (05.00), you have to start at the bottom, with the units. There are carried when the number 19 units is exceeded, passing to the higher level.

04 X 01 (Series 20) = 04 + 01 (taken) = 05 (series 20)

04 X 05 (units) =.....................

Now a slightly more complicated example with horizontal numbers:

We take 19 scores (19 X 20 = 380) and one unit (= 381).

If we want to multiply 19.01 (381 in the decimal system) by two, we get 01.18.02 (762 in the decimal system). That is, 400 + 360 + 2.

19.01 (multiplicating)

X 02 (multiplier)

----

01.18.02 (product)

If we want to multiply 19.01 (381 in decimal) by three, we get 02.17.03 (1 143 in decimal). That is, 800 + 340 + 3.

19.01 (multiplicating)

X 03 (multiplier)

-...

02.17.03 (product)

The procedure is as follows.

1) We start by multiplying the units (02 X 01) or (03 X 01) and write down the product in each operation.

2) Then we move on to the next series:

02 X 19 = 38 → and since 18 exceeds 20, we put 18. And there are also 20 left for the series of 400 (which are equivalent to 01).

03 X 19 = 57 → And since 17 exceeds 40, we put 17. And there are also 40 left for the series of 400 (which is equivalent to 02).

Time tables in the vigesimal system

They are a very useful accessory when dividing.

Division in the vigesimal system

Division is solved in the same way in the vigesimal system, but a caveat must be made with the decimal part because the numbers do not square with the method of the decimal system:

1) Decimal system.

77.5 (dividendo): 25 (divisor)

025 (partial) 3.1 (quotient or result)

0 (final)

2) Vigesimal system.

03.17, 10 (dividendo): 01.05 (divisor)

03.02 (patient or outcome)

-03.15

02.10 (partial)

-02.10

00 (final)

As we can see, non-integer numbers do not behave as expected. But this is explained below.

The fractional part in the vigesimal system

Let's separate the fractional part from the integer part by a comma.

In the decimal system, the unit is divided into 10 parts (or tenths) so if we add five tenths and five tenths we get the unit. We can also add fifty hundredths plus fifty hundredths: 0.50 + 0.50 = 1.

In the vigesimal system, the unit is divided into 20 parts, so 0.10 is half the unit.

So really, the fractional part of the division in the previous section would be 00.10. Because 00.10 + 00.10 gives 01.00.

Therefore, the decimal quotient 3.10 is equivalent to the vigesimal quotient 03.02.

And it is that 10 parts of 100 (decimal system) are equivalent to 2 parts of 20 (vigesimal system), which is demonstrated with a simple rule of three:

10 --- 100

02 --- X = 20

If by decimal we understand fraction, broken or part, there is no doubt that we are dealing with decimal numbers. In The vigesimal system does not exist tenths, hundredths or thousandths, but there are decimals. Because when a mathematician says in the decimal system that 0.5 is five tenths, or fifty hundredths, or five hundred thousandths... he is referring to a value that represents half of the unit and the same thing happens when a mathematician in the vigesimal system says that 0.10 is half a unit. Both mathematicians are expressing the same idea.

_

Decimal break	Patient decimal system	Vigesimal broken	Recent Vigesimal System
1/100	0.01	01/05.00	00,00.04
2/100	0.02	02/05.00	00,00.08
3/100	0.03	03/05.00	00,00.12
4/100	0.04	04/05.00	00,00.16
5/100	0.05	05/05.00	00,01
6/100	0.06	06/05.00	00,01.04
7/100	0.07	07/05.00	00,01.08
8/100	0.08	08/05.00	00,01.12
9/100	0.09	09/05.00	00.01.16
10/100	0.10	10/05.00	00,02
11/100	0.11	11/05.00	00,02.04
12/100	0.12	12/05.00	00,02.08
13/100	0.13	13/05.00	00.02.12
14/100	0.14	14/05.00	00,02.16
15/100	0.15	15/05.00	00.03
16/100	0.16	16/05.00	00,03.04
17/100	0.17	17/05.00	00,03.08
18/100	0.18	18/05.00	00,03.12
19/100	0.19	19/05.00	00,03.16
20/100	0.20	01.00/05.00	00,04
21/100	0.21	01.01/05.00	00.04.04
22/100	0.22	01.02/05.00	00,04.08
23/100	0.23	01.03/05.00	00,04.12
24/100	0.24	01.04/05.00	00.04.16
25/100	0.25	01.05/05.00	00,05
26/100	0.26	01.06/05.00	00,05.04
27/100	0.27	01.07/05.00	00,05.08
28/100	0.28	01.08/05.00	00,05.12
29/100	0.29	01.09/05.00	00.05.16
30/100	0.30	01.10/05.00	00,06
31/100	0.31	01.11/05.00	00,06.04
32/100	32	01.12/05.00	00,06.08
...	...	...	...
60/100	0.60	03.00/05.00	00.12
61/100	0.61	03.01/05.00	00,12.04
62/100	0.62	03.02/05.00	00.12.08
...	...	..	...
72/100	0.72	03.12/05.00	00,14.08
...	...	..	...
82/100	0.82	04.02/05.00	00,16.08
...	...	..	...
85/100	0.85	04.05/05.00	00,18
...	...	..	...
95/100	0.95	04.15/05.00	00,19
96/100	0.96	04.16/05.00	00,19.04
97/100	0.97	04.17/05.00	00,19.08
98/100	0.98	04.18/05.00	00,19.12
99/100	0.99	04.19/05.00	00,19.16
100/100	1,00	05.00/05.00	01,00

If we take 0.98 (from the decimal system) we can easily convert it to the vigesimal system:

1) We take the last digit after the comma, 8, and multiply it by 4 (= 32). Since it goes from 20 to 12, we write down “.12”. And we have a unit of 20.

2) Then we take the digit 9, which is attached to the comma and multiply it by 2 (= 18) and add the carried one (18 + 1 = 19) and write down the product on the left «00,19.12 ».

So if we want to divide 55/4 (= 13.75), we can represent it like this 02.15/04 = 13.15 in the vigesimal system.

And the development of the division is as follows:

02.15 (dividendo)	: 04 (divisor)
-02.12	13 (because 13 X 04 = 02.12),15 (because 15 X 04 = 03.00)
00.03.00 (partial)
-03.00
00.00 (final)

Note that the decimal is the fraction of the last digit, so 20 + 0.5 = 20.5.

Decimals in the vigesimal system are expressed in base 20, but they do not lose their decimal character, as has been shown. Otherwise the Native American could not divide correctly. Some mistakenly believe that 13.75 (decimal) represents 13.02.15. That is a very serious error that supposes to write the whole numbers and the fractional part with the same criteria. 0.75 indicates 3/4 of the unit of the decimal system. Any decimal quotient, whether expressed decimal or vigesimally, should not lose sight of that, that it is a quotient and that it is related to a fraction of the unit. And it has served to historically present Native American mathematics as inferior. Of that, nothing.

Conversion of the decimal quotient from the decimal system to the vigesimal system and vice versa

We have seen that the decimal quotient in the decimal system has a multiplicity of digits that represent the tenths, hundredths, thousandths... etc. For every tenth of the decimal system there are two units in the vigesimal system. It is logical, because the unit of the decimal system has 10 units and that of the vigesimal system has 20.

For every hundredth in the decimal system there are four in the vigesimal system. So we multiply by four.

For every thousandth in the decimal system there are eight in the vigesimal system. So we multiply by 8.

Decimal break	Patient decimal system	Vigesimal broken	Recent Vigesimal System
9/1000	0.009	09/02.10.00	00,00.03.12

The development of this vigesimal division is as follows:

09.00.00 (dividendo)	: 02.10.00(divisor)
01.10.00.00 (partial)	00,00.03.12 (quotient)
-01.10.00.00
00.00 (final)

Explanation of why we add 12 to the quotient:

01.10.00.00 = (1 X 8000) + (10 X 400) + 0 + 0 = 12000

And that, divided by 02.10.00 = (2 X 400) + (10 X 20) + 0 = 1000, gives 12.

That is, we have searched for a number that multiplied by 02 (of the divisor) is close to 01.10 (of the partial remainder) for the quotient. For this we have taken the auxiliary multiplication tables from 10 to 19, and we have seen that 15 is passed by the divisor. The same goes for 14 and 13.

Since mathematicians are always looking for shortcuts and in the absence of vigesimal calculators on the market, it seems logical to convert a vigesimal division to a decimal and then pass the quotient to the vigesimal system. It's a fair shortcut. To do this, the procedure is as follows:

Vigesimal broken	Decimal break
09/02.10.00	9/(800+200)

Parts of the decimal quotient

In the base ten decimal system, we call the first number after the comma a tenth. But if there are two numbers after the comma (0'45) tenths that there are forty-five hundredths. In other words, the four has a value of forty hundredths or four tenths. Or what is the same, the first number after the comma can express both tenths and hundredths or thousandths..., etc.

The same thing happens in the vigesimal system:

* 0.60 (base decimal system 10: six tenths, zero hundredths or 60 hundredths) → 00,01.04 (one on four tetracentesimas or a twentieth, four tetracentesimas).

The tenths, hundredths and thousandths, when expressed in vigesimal terms, are represented in another way. For each of the ten parts of the unit, in the vigesimal system there are twenty. That is why we multiply the first number after the comma by two. For every hundredth there are four hundred parts of units in the vigesimal system, so we multiply them by four. For every thousandth there are eight thousand parts of the unit, so we multiply them by eight when converting. The multiplication is done starting from right to left, to adequately compute the carried.

* 0.5 + 0.5 = 1 (decimal system)

* 00.10 + 00.10 = 1 (vigesimal system)

* 6/100 → 0.06

* 06/05.00→ 00,01.04

We can divide the decimal unit into other quantities, so we would have ten thousandths, hundred thousandths, millionths, ten millionths, hundred millionths, billionths, ten billionths, hundred billionths, billionths, ten billionths, hundred billionths..., trillionths..., quadrillionths..., quintillionths... that are written together.

In Nahuatl there is a suffix «-can» which means part.

Ce: One → Ceccan: Part

Matlactli: Ten → Mahtlaccan: Ten parts → Cemmahtlaccan (décima)

Two tenths are said "ommatlaccan".

And each of the 20 parts of the unit, which in Spanish are called «twentyths», is called «cempohualcan».

Value of zero in the decimal quotient expressed in base 20 (or vigesimally)

When we express the decimal quotient in base 10, we find that 0'1 indicates both one tenth, ten hundredths, and one hundred thousandths. We can put as many zeros as we want to the right. This occurs because ten hundredths is one tenth and ten thousandths is one hundredth.

When we express the decimal quotient in base 20, we see that the system does not operate in the same way.

* 0.06 → 00.12 (six hundredths or twelve twentieths)

* 0,60 → 00,01.04 (six tenths, zero hundredths) (veinticuatro tetracentésimas or a twentieth, four tetracentesimas)

But we can say that ten hundredths is one tenth: 10 X 00.00.04 = 00.02. Because ten times four is forty, so we put double zero in that series and we carry two units (of value 20), which we put in the series on the left.

And we can put as many zeros on the right as we want to indicate that there are zero series on the right, which fragment the unit into more units (8000, 16000...).

In the vigesimal system, trailing zeros indicate that there are no more series to the right. In the base 10 decimal system, zeros mean the opposite, that there are more series to the right.

The square root in the vigesimal system

First we will put the decimal version of the problem.

21 X 21 = 441 → 212 = 441 → √441 = 21.

√441 (radiation)	= 21 (result line)
-4	41 X 1
041
-41
0 (chuckles)

And now the same operation in the vigesimal system.

√01.02.01 (radiation)	= 01.01 (result line)
-01	02.01 X 01
00. 02.01
-02.01
00.00 (chuckles)

Flats in the vigesimal system

The mathematical representation of a decimal number is very simple:

1/n

The fractions are decimal numbers. The number one indicates the unit (valid for both the decimal and vigesimal systems). The letter n represents any number.

When a Native American divides a pie among four companions, he does not break 20 pieces and give each one five. When a European divides a cake by four, he does not divide 10 parts or subdivide some parts by 10. Both divide the cake into four parts, into four fractions. We cannot say that the decimal system is superior to the vigesimal system or vice versa. Each one has its advantages and disadvantages.

Same if you split it in half. There is no doubt that the Native Americans operated with bankruptcies.

1/2 = 0.5 (decimal system)

01/02 = 00.10 (vigesimal system)

Sum of fractions

03/05 + 02/07

=

01.01/01.15 + 10/01.15

=

01.11/01.15

The number π (“pi”) in the vigesimal system

Greek letters pi. Symbol adopted in 1706 by William Jones and popularized by Leonhard Euler.

The number π is a coefficient that multiplied by the diameter indicates the length of the circumference. That is, three times the diameter is close to the length of the circumference, but falls short. Actually you have to multiply the diameter by 3.14159...

Decimal system:

π = 3,14159...

Vigesimal system:

π = 03,02.16.08.18.04...

Explanation of its obtaining:

STEP 1.

Decimal quotient	Multiplier	Patient 20simal
0.1 (decimation)	X 2	00,02 (thousands)
0.01 (thousand)	X 4	00,00.04 (thousands)
0.001 (thousand)	X 8	00,00.00.08 (ochomilésimas)
0.0001 (diezmilésima)	X 16	00,00.00.00.16
0.00001 (scientific)	X 32	00,00.00.00.01.12
...	...	...

STEP 2.

We have to take into account the carried ones.

The length of the circumference.

L = 2 X π X r

The area of the circle.

A = π X r2

European languages

• In euskera the numbering system uses the vigesimal system: hogei 'veinte', Hogeita hamar 'veinte and ten', berrogei 'two twenties', Berrogeita hamar 'two and ten'... According to the German linguist Theo Vennemann, the vigesimal system sporadically found in certain languages of Europe would be an influence of a Basque substratum, which would then have spread to other languages, mainly the Celt, and through it to languages such as French and Danish. However, according to Karl Menninger, the vigesimal system originated from the Normans and through them extended to Western Europe.
• Although the numbering system of the indoeuropeo is decimal, in many European languages there are residues of the vigesimal system, attributed to the cellar system, which as mentioned above could have been influenced by pre-indo-European languages of Europe:
  • Twenty.vingt) is the base number in French. For example, quatre-vingts means four times twenty (4×20), that's 80. In the Middle Ages it was said "vint et dis" (30), "deux vins" (40), "trois vins" (60). Saint Louis, IX of France, founded the Hospice of the 300 blind, "l'Ospice des Quinze-vingts". At the end of the Middle Ages the Latin system, "trente", "quarante", "cinquante", "soixante", 30, 40, 50 and 60. Vaugelas and Ménage, in the seventeenth century, achieve that the Academy and Loa authors of dictionaries adopt "soixante-dix", "quatre-vingts", "quatre-vingt-dix" with preference to "septante", "octante", and "nonante", 70, 80 and 90, respectively. Both notions exist in the Dictionary of the French Academy. The first are regular in France, the second are used in some places of the East and the French Middle Ages, and are official in Belgium, French-speaking Switzerland and Quebec, and even all the official instructions of 1945 for the learning of the calculation were advised throughout France. It is the use that has prevailed.
  • Twenty is also the base number in the Danish language. Three. (abbreviation of 3indstyve) is three times twenty (3×20), or 60; firs (abbreviation of firsindstyve) means four times twenty (4×20), or 80. Halvtreds means (3 – 1⁄2) × 20, that is, 50; halvfjerds means (4 – 1⁄2) × 20, that is, 70; and halvfems means (5 – 1⁄2) × 20, that is, 90.
  • Twenty.ugain) is also a base number in the Welsh language, although in the end of the 20th century the decimal system was preferred, making the vigesimal system become "traditional". Deugain is twice twenty (2×20), i.e. 40. Same way trigain It's 3 by 20, that's 60.
  • In the old British monetary system, there were twenty shillings in every sterling pound. Similarly, in English, people have counted for twenty (scoreshistorically, as in the famous Gettysburg Speech of Abraham Lincoln, who begins with the quote "Four score and seven years ago..."Four twenty-seven years ago..."),

Asian languages

• In santali, one of the worldly languages of India, "five" is expressed by bār isī gälliterally "two twenty ten." Similarly, in Didei, another worldly language in India, complex numerals use the decimal system until 19 and a decimal-vigesimal system up to 399.

South American languages

• The Muiscas used a base system 20

Mesoamerican languages

• In the Mesoamerican linguistic area, there are several linguistic families such as the utoaztec languages, the Mayan languages, the Otomanguean languages or the non-genetically related mixed-zoquean languages that nevertheless present several typical traits as a result sprachbund For long contact. One of the typical traits actually shared is the 20.
• The Maya numeration was a base system twenty.

The Zero

Traditionally, the use of zero has been granted to the Mayans, who have been considered more advanced than the Nahuas.

• Mayan civilization was the first in America to devise zero. This was necessary for their numbering because the Mayas had a positional system, that is, a numbering system in which each symbol has a different value according to the position it occupies. The zero symbol is represented by a snail (sheet or seed), which indicates that there are no units.

But perhaps credit should be given to Mesoamerican man and not to the Maya. Because samples have been found in different sites that prove that Mesoamerican cultures had a common heritage. The vigesimal numbering system is part of that common heritage.

Vigesimal powers in Mayan and Nahuatl language

Vigesimal Powers in Mayan and Nahuatl
Number	Spanish	Maya	Nahuatl (modern spelling)	Classical Nahuatl	Raíz náhuatl	Mexica Pictogram
1	One	Hun	Separate	Ce	Ce
20	Twenty	K'áal	Sempouali	Cempohualli (Cempoalli)	Pohualli
400	Four hundred	Bak	Sentzontli	Centzontli	Tzontli
8000	Eight thousand	Pic	Senxikipili	Cenxiquipilli	Xiquipilli
160,000	One hundred and sixty thousand	Calab	Sempoualxikipili	Cempohualxiquipilli	Pohualquipilli
3,200,000	Three million two hundred thousand	Kinchil	Sentzonxikipili	Centzonxiquipilli	Tzonxiquipilli
64,000.000	Sixty-four million	Alau	Sempoualtzonxikipili	Cempohualtzonxiquipilli	Pohualtzonxiquipilli

Numbering in units of twenty

This table shows Mayan numbering and numerals in the Mayan language, Nahuatl in modern orthography, and in Classical Nahuatl.

From one to ten (1 - 10)
1 (one)	2 (two)	3 (three)	4 (four)	5 (Cinco)	6 (six)	7 (seven)	8 (eight)	9 (nine)	10 (ten)
Hun	Ka'ah	Oil	Kan	Ho'	Wak	Uk	Waxak	Bolon	Lahun
Separate	Ome	Yeyi	Naui	Makuili	Chikuasen	Chikome	Chikueyi	Chiknaui	Majtlaktli
Ce	Ome	Yei	Nahui	Macuilli	Chicuace	Boy me	Chicuei	Chicnahui	Matlactli
From eleven to twenty (11 - 20)
11	12	13	14	15	16	17	18	19	20
Buluk	Lahka'a	Oox lahun	Kan lahun	Ho' lahun	Wak lahun	Uk lahun	Waxak lahun	Bolon lahun	Hun k'áal
Majtlaktli onse	Majtlaktli omome	Majtlaktli omeyi	Majtlaktli onnaui	Kaxtoli	Kaxtoli onse	Kaxtoli omome	Kaxtoli omeyi	Kaxtoli onnaui	Sempouali
Matlactli huan ce	Matlactli huan ome	Matlactli huan yei	Matlactli huan nahui	Caxtolli	Caxtolli huan ce ce	Caxtolli huan ome	Caxtolli huan yei	Caxtolli huan nahui	Cempohualli
From twenty-one to thirty (21 - 30)
21	22	23	24	25	26	27	28	29	30
Hump'éel katak hun k'áal	Ka'ah katak hun k'áal	Óox katak hun k'áal	Kan katak hun k'áal	Ho' katak hun k'áal	Wak katak hun k'áal	Uk katak hun k'áal	Waxak katak hun k'áal	Bolon katak hun k'áal	Lahun katak hun k'áal
Sempouali onse	Sempouali omome	Sempouali omeyi	Sempouali onnaui	Sempouali ommakuili	Sempouali onchikuasen	Sempouali onchikome	Sempouali onchikueyi	Sempouali onchiknaui	Sempouali ommajtlaktli
Cempohualli huan ce	Cempohualli huan ome	Cempohualli huan yei	Cempohualli huan nahui	Cempohualli huan macuilli	Cempohualli huan chicuace	Cempohualli huan chicome	Cempohualli huan chicuei	Cempohualli huan chicnahui	Cempohualli huan matlactli
From thirty-one to forty (31 - 40)
31	32	33	34	35	36	37	38	39	40
Buluk katak hun k'áal	Lahka'a katak hun k'áal	Óox lahun katak hun k'áal	Kan lahun katak hun k'áal	Ho' lahun katak hun k'áal	Wak lahun katak hun k'áal	Uk lahun katak hun k'áal	Waxak lahun katak hun k'áal	Bolon lahun katak hun k'áal	Ka' k'áal
Sempouali ommajtlaktli onse	Sempouali ommajtlaktli omome	Sempouali ommajtlaktli omeyi	Sempouali ommajtlaktli onnaui	Sempouali onkaxtoli	Sempouali onkaxtoli onse	Sempouali onkaxtoli omome	Sempouali onkaxtoli omeyi	Sempouali onkaxtoli onnaui	Ompouali
Cempohualli huan matlactli huan ce	Cempohualli huan matlactli huan ome	Cempohualli huan matlactli huan yei	Cempohualli huan matlactli huan nahui	Cempohualli huan caxtolli	Cempohualli huan caxtolli huan ce ce	Cempohualli huan caxtolli huan ome	Cempohualli huan caxtolli huan yei	Cempohualli huan caxtolli huan nahui	Ompohualli
From twenty to two hundred in steps of twenty (20 - 200)
20	40	60	80	100	120	140	160	180	200
Hun k'áal	Ka' k'áal	Oox k'áal	Kan k'áal	Ho' k'áal	Wak k'áal	Uk k'áal	Waxak k'aal	Bolon k'áal	Lahun k'áal
Sempouali	Ompouali	Yepouali	Naupouali	Makuilpouali	Chikuasempouali	Chikompouali	Chikuepouali	Chiknaupouali	Majtlakpouali
Cempohualli	Ompohualli	Yeipohualli	Nauhpohualli	Macuilpohualli	Chicuacepohualli	Chicomepohualli	Chicueipohualli	Chicnahuipohualli	Matlacpohualli
From two hundred and twenty to four hundred in steps of twenty (220 - 400)
220	240	260	280	300	320	340	360	380	400
Buluk k'áal	Lahka'a k'áal	Oox lahun k'áal	Kan lahun k'áal	Ho' lahun k'áal	Wak lahun k'áal	Uk lahun k'áal	Waxak lahun k'áal	Bolon lahun k'áal	Hun bak
Majtlaktli onse pouali	Majtlaktli omome pouali	Majtlaktli omeyi pouali	Majtlaktli onnaui pouali	Kaxtolpouali	Kaxtolli onse pouali	Kaxtolli omome pouali	Kaxtolli omeyi pouali	Kaxtolli onnaui pouali	Sentsontli
Matlactli huan ce pohualli	Matlactli huan ome pohualli	Matlactli huan yei pohualli	Matlactli huan nahui pohualli	Caxtolpohualli	Caxtolli huan ce pohualli	Caxtolli huan ome pohualli	Caxtolli huan yei pohualli	Caxtolli huan nahui pohualli	Centzontli