Vectorial space

This article is aimed at providing rigorous and abstract treatment of the concept of vector space. For a more accessible introduction to the concept, see Vector

Artistic representation of a vector space.

In linear algebra, a vector space (or also called a linear space) is an algebraic structure created from a non-empty set, an inner operation (called sum, defined for the elements of the set) and an external operation (called product by a scalar, defined between said set and another set, with field structure) that satisfies 8 properties fundamental.

Elements of a vector space are called vectors and elements of the field are called scalars.

History

Historically, the first ideas that led to modern vector spaces date back to the 17th century: analytic geometry, matrices, and systems of linear equations.

Vector spaces are derived from affine geometry through the input of coordinates in plane or three-dimensional space. Around 1636, the French mathematicians Descartes and Fermat laid the foundations of analytic geometry by linking the solutions of an equation in two variables to the determination of a plane curve. To achieve a geometric solution without using coordinates, Bernhard Bolzano introduced in 1804 certain operations on points, lines, and planes, which are predecessors of vectors. This work made use of August Ferdinand Möbius's 1827 concept of barycentric coordinates.

The first modern and axiomatic formulation is due to Giuseppe Peano, at the end of the XIX century. The next advances in the theory of vector spaces come from functional analysis, mainly of spaces of functions. Functional Analysis problems required solving problems about convergence. This was done by endowing the vector spaces with a suitable topology, allowing issues of proximity and continuity to be taken into account. These topological vector spaces, in particular the Banach spaces and the Hilbert spaces have a richer and more elaborate theory.

The origin of the definition of the vectors is the definition of bipoint by Giusto Bellavitis, which is an oriented segment, one end of which is the origin and the other an objective. Vectors were reconsidered with the introduction of Argand and Hamilton's complex numbers and the creation of quaternions by the latter (Hamilton was also the one who invented the name vector). They are elements of R² and R⁴; treatment by linear combinations dates back to Laguerre in 1867, who also defined systems of linear equations.

In 1857, Cayley introduced matrix notation which allows for a harmonization and simplification of linear maps. Around the same time, Grassmann studied the barycentric calculus pioneered by Möbius. He envisioned sets of abstract objects endowed with operations.In his work, the concepts of linear independence and dimension, as well as scalar product are present. Actually Grassmann's work of 1844 exceeds the framework of vector spaces, since taking multiplication into account, too, led him to what are today called algebras. The Italian mathematician Peano gave the first modern definition of vector spaces and linear maps in 1888.

An important development of vector spaces is due to the construction of function spaces by Henri Lebesgue. This was later formalized by Banach in his 1920 doctoral thesis and by Hilbert. At this time, algebra and the new field of functional analysis began to interact, in particular with key concepts such as spaces of p-integrable functions and Hilbert spaces. Also at this time, the first studies on vector spaces of infinite dimensions were made.

Vector spaces have applications in other branches of mathematics, science, and engineering. They are used in methods such as Fourier series, which is used in modern image and sound compression routines, or provide the framework for solving partial differential equations. In addition, vector spaces provide a coordinate-free abstract way of dealing with geometric and physical objects, such as tensors, which in turn allow the study of local properties of manifolds by linearization techniques.

Notation

Given a vector space V{displaystyle V} on a body K{displaystyle K}, the elements of V{displaystyle V} and those of K{displaystyle K}.

The elements of V{displaystyle V} They tend to score.

u,v,w{displaystyle mathbf {u}mathbf {v}mathbf {w}}

and are called vectors.

Depending on the sources that are consulted, it is also common to denote them by

u! ! ,v! ! ,w! ! {displaystyle {bar {u}},{bar {v}},{bar {w}

and if the text is about physics then they are usually denoted by

u→ → ,v→ → ,w→ → {displaystyle {vec {u}},{vec {v}},{vec {w}}}}

While the elements of K{displaystyle K} denotes as

a,b,α α ,β β {displaystyle a,b,alphabeta }

and are called scalars.

Definition

A vector space on a body K{displaystyle K} (like the body of real numbers or complex numbers) is a non-empty set, let's say V{displaystyle V}with two operations for which it will be closed:

Summa+:V× × V→ → V(u,v) u+v{displaystyle {begin{array}{llccl}{mbox{Suma}}{mbox{Suma}}{Vtimes V}{rightarrow &{V}{V} expose(mathbf {u}mathbf {v}}{v}}}{mathbf}}{mathbf {v}}}}}}}}}}}}}}}}{end

internal operation such that:

• Have the commutative property:

u+v=v+u,Русский Русский u,v한 한 V{displaystyle mathbf {u} +mathbf {v} =mathbf {v} +mathbf {u}quad forall ;mathbf {u}mathbf {v} in V}

• Have the associative property:

u+(v+w)=(u+v)+w,Русский Русский u,v,w한 한 V{displaystyle mathbf {u} +(mathbf {v} +mathbf {w})=(mathbf {u} +mathbf {v})+mathbf {w}quad forall ;mathbf {u}mathbf {v}mathbf {w}mathbf {w}{w}mathbf {w}{w}mathbf {w}

• Exist the neutral element:

consuming consuming e한 한 V:{displaystyle exists ;mathbf {e} in {}V:} u+e=u,{displaystyle mathbf {u} +mathbf {e} =mathbf {u}} Русский Русский u한 한 V{displaystyle forall ;mathbf {u} in V}

• Exist the opposite element:

Русский Русский u한 한 V,consuming consuming − − u한 한 V:{displaystyle forall ;mathbf {u} in V,quad exists -mathbf {u} in {V:} u+(− − u)=e{displaystyle mathbf {u} +(-mathbf {u})=mathbf {e} }

And have the operation product by a scalar:

Output⋅ ⋅ :K× × V→ → V(a,u) a⋅ ⋅ u{displaystyle {begin{array}{llccl}{mbox{{Product}}}{cdot {}: fake{Ktimes V}{rightarrow &{V} pretend(a,mathbf {u}}}}{mapsto &acdot mathbf {u} end{array}}}}}}}}}}}}}}}}}}

outer operation such that:

• Have the associative property:

a⋅ ⋅ (b⋅ ⋅ u)=(a⋅ ⋅ b)⋅ ⋅ u,{displaystyle {mathit {a}}cdot ({mathit {b}cdot mathbf {u})=({mathit {a}}}cdot {mathit {b}})cdot mathbf {u}}} Русский Русский a,b한 한 K,{displaystyle forall ;{mathit {a}},{mathit {b}in {}K,} Русский Русский u한 한 V{displaystyle forall ;mathbf {u} in V}

• Exist the neutral element:

consuming consuming e한 한 K:{displaystyle exists ein {K}:} e⋅ ⋅ u=u,{displaystyle ecdot mathbf {u} =mathbf {u} Русский Русский u한 한 V{displaystyle forall ;mathbf {u} in V}

• Have the distribution property regarding the vector sum:

a⋅ ⋅ (u+v)=a⋅ ⋅ u+a⋅ ⋅ v,{displaystyle {mathit {a}}cdot (mathbf {u} +mathbf {v}={mathit {a}}cdot mathbf {u} +{mathit {a}}}cdot mathbf {v}} Русский Русский a한 한 K,{displaystyle forall ;{mathit {a}}in K,} Русский Русский u,v한 한 V{displaystyle forall ;mathbf {u}mathbf {v} in V}

• Have the distribution property with respect to the sum scaling:

(a+b)⋅ ⋅ u=a⋅ ⋅ u+b⋅ ⋅ u,{displaystyle ({mathit {a}}+{mathit {b}})cdot mathbf {u} ={mathit {a}}cdot mathbf {u} +{mathit {b}}}cdot mathbf {u}} Русский Русский a,b한 한 K,{displaystyle forall {}{mathit {a}},{mathit {b}in {}K,} Русский Русский u한 한 V{displaystyle forall ;mathbf {u} in V}

Observations

The name of the two operations does not condition the definition of a vector space, so it is common to find translations of works in which multiplication is used for the product and addition for addition, using the distinctions of arithmetic.

To demonstrate that a set V{displaystyle V_{}^{}{}}} is a vector space:

• It is if your two operations, for example Δ Δ (V,V){displaystyle odot (V,V)} and ↓ ↓ (V,K),{displaystyle ast (V,K),} support a redefinition of the type +(V,V)=Δ Δ (V,V){displaystyle +(V,V)=odot (V,V)} and ⋅ ⋅ (K,V)=↓ ↓ (V,K){displaystyle cdot (K,V)=ast (V,K)} complying with the 8 conditions required.
• If we knew that V{displaystyle V_{}^{}{}}} is a commutative or abelian group regarding the sum we would already have tested the sections 1, 2, 3 and 4.
• If we know that the product is an action on the left V{displaystyle V_{}^{}{}}} We'd have tested the sections. 5 and 6.
• If not, the opposite is said:

avI was. I was. va{displaystyle {mathit {a}}mathbf {v} neq mathbf {v} {mathit {a}}}}.

Properties

Unicity of the neutral vector of the property 3

Suppose the neutral is not unique, that is, 01{displaystyle mathbf {0_{1}} } and 02{displaystyle mathbf {0_{2}} } Two neutral vectors, then: u+01=uu+02=u!⇒ ⇒ {displaystyle left.{begin{array}{l}mathbf {u} +mathbf {0_{1}} =mathbf {u} \mathbf {u} +mathbf {0_{0}}} =mathbf {u} end{array}rightRightarrow } u+01=u+02⇒ ⇒ {displaystyle mathbf {u} +mathbf {0_{1}}} =mathbf {u} +mathbf {0_{2}}}} ¶¶ 01=02⇒ ⇒ {displaystyle mathbf {0_{1}} =mathbf {0_{2}}}} ¶¶ consuming consuming !0한 한 V{displaystyle exists};mathbf {0} in V}

Unique of the opposite vector of the property 4

Suppose the opposite is not unique, i.e. − − u1{displaystyle mathbf {-u_{1}} } and − − u2{displaystyle mathbf {-u_{2}}} } two opposite vectors u{displaystyle mathbf {u} }, then, as the neutral is unique: u− − u1=0u− − u2=0!⇒ ⇒ {displaystyle left.{begin{array}{l}mathbf {u} -mathbf {u_{1}} =mathbf {0} \mathbf {u} -mathbf {u_{u_{2}} =mathbf {0} end{array}rightRightarrow } u− − u1=u− − u2⇒ ⇒ {displaystyle mathbf {u} -mathbf {u_{1}}} =mathbf {u} -mathbf {u_{2}}}} ¶¶ − − u1=− − u2⇒ ⇒ {displaystyle -mathbf {u_{1}} =-mathbf {u_{2}}} ¶¶ consuming consuming !− − u한 한 V{displaystyle exists}-mathbf {u} in V}

Oneness of the element 1{displaystyle}{}{}{displaystyle} in the body K{displaystyle K_{}^{}{}}}

Suppose 1 is not unique, i.e. 11{displaystyle {mathit {1_{1}}}{;} and 12{displaystyle {mathit {1_{2}}}}{;} Two units, then: a⋅ ⋅ 11=aa⋅ ⋅ 12=a!⇒ ⇒ {displaystyle left.{begin{array}{l}{mathit {a}{cdot {mathit {1_{1}}}}{mathit {a}}}{mathit {a}}{mathit {a}}}{cdot {mathit {1}}}}{{right}{end{array}} a⋅ ⋅ 11=a⋅ ⋅ 12⇒ ⇒ {displaystyle {mathit {a}}cdot {mathit {1_{1}}}}{mathit {a}}{cdot {mathit {1_{2}}}}}}{Rightarrow } 11=12⇒ ⇒ {displaystyle {mathit {1_{1}}}}={mathit {1_{2}}}}{Rightarrow } consuming consuming !1한 한 K{displaystyle exists}{mathit {1}in K}

Unicity of the reverse element in the body K{displaystyle K_{}^{}{}}}

Suppose the reverse a− − 1{displaystyle a_{}^{-1}} from a, it's not unique, that is, a1− − 1{displaystyle a_{1⁄2}{-1}} and a2− − 1{displaystyle a_{2}{-1}} two opposites of a{displaystyle a_, then, as the neutral is unique: a⋅ ⋅ a1− − 1=1a⋅ ⋅ a2− − 1=1!⇒ ⇒ {displaystyle left.{begin{array}{l}{mathit {a}{cdot {mathit {a_{1}{1}{mathit {1}}{mathit {a}}}{mathit {a}}}{cdot {mathit {a_{2}{1}{math}}}{math}}}}}{mathre}}}}{ a⋅ ⋅ a1− − 1=a⋅ ⋅ a2− − 1⇒ ⇒ {displaystyle {mathit {a}}{cdot {mathit {a_{1⁄2}}}}}}}{{mathit {a}}cdot {mathit {a_{2}{1⁄2}}}{Rightarrow }} a1− − 1=a2− − 1⇒ ⇒ {displaystyle {mathit {a_{1}{1}}}{mathit {a_{2}{1}{1}}}{Rightarrow } consuming consuming !a− − 1한 한 K{displaystyle exists}{mathit {a^{-1}}}in K}

Product of a scale by the neutral vector

a⋅ ⋅ u={displaystyle {mathit {a}}cdot mathbf {u} = a⋅ ⋅ (u+0)={displaystyle {mathit {a}}cdot (mathbf {u} +mathbf {0})=} a⋅ ⋅ u+a⋅ ⋅ 0⇒ ⇒ {displaystyle {mathit {a}}cdot mathbf {u} +{mathit {a}cdot mathbf {0} ¶¶ a⋅ ⋅ 0=0{displaystyle {mathit {a}}cdot mathbf {0} =mathbf {0} }

Climbing product 0 by a vector

u={displaystyle mathbf {u} =} 1⋅ ⋅ u={displaystyle {mathit {1}}cdot mathbf {u} = (1+0)⋅ ⋅ u={displaystyle ({mathit {1}}+{mathit {0}}})cdot mathbf {u} =} 1⋅ ⋅ u+0⋅ ⋅ u={displaystyle {mathit {1}}cdot mathbf {u} +{mathit {0}cdot mathbf {u} =} u+0⋅ ⋅ u⇒ ⇒ {displaystyle mathbf {u} +{mathit {0}}cdot mathbf {u} Rightarrow } 0⋅ ⋅ u={displaystyle {mathit {0}}cdot mathbf {u} = 0{displaystyle mathbf {0} }

Yeah. a⋅ ⋅ u=0⇒ ⇒ {displaystyle {mathit {a}}cdot mathbf {u} =mathbf {0} ¶¶ a=0 u=0.{displaystyle {mathit {a}}={mathit {0}}}quad lor quad mathbf {u} =mathbf {0}. !

• Yeah. a=0,{displaystyle a_{}^{}=0,} That's right.
• Yeah. aI was. I was. 0,{displaystyle aneq 0,} Then:

consuming consuming !a− − 1한 한 K:{displaystyle exists};a^{-1}in K:} a− − 1a=1⇒ ⇒ {displaystyle a^{-1}a=1Rightarrow } u={displaystyle u=} 1u={displaystyle 1u=} (a− − 1a)u={displaystyle (a^{-1}a)u=} a− − 1(au)={displaystyle a^{-1}(au)=} a− − 10=0⇒ ⇒ {displaystyle a^{-1}0=0Rightarrow } u=0.{displaystyle u_{}^{}=0. !

Notation

− − au=− − (au){displaystyle -au=-(au),}.

Observation

− − au=(− − a)u=a(− − u){displaystyle -au=(-a)u=a(-u),}

• Yeah. au+a(− − u)=a(u− − u)=a0=0⇒ ⇒ {displaystyle au+a(-u)=a(u-u)=a0=0Rightarrow } a(− − u)=− − au{displaystyle a(-u)=-au,}
• Yeah. au+(− − a)u=(a− − a)u=0u=0⇒ ⇒ {displaystyle au+(-a)u=(a-a)u=0u=0Rightarrow } (− − a)u=− − au{displaystyle (-a)u=-au,}

First example with demo

You want to prove that R2{displaystyle mathbb {R} ^{2}} It's a vector space over R{displaystyle mathbb {R} }

Yeah. R2{displaystyle mathbb {R} ^{2}} play the role V{displaystyle V;} and R{displaystyle mathbb {R} } of K{displaystyle K;}:

The elements:

u한 한 V=R2=R× × R{displaystyle mathbf {u} in V=mathbb {R} ^{2}=mathbb {R} times {mathbb {R} }

are, generically:

u=(ux,uand){displaystyle mathbf {u} =(u_{x},u_{y}}}

that is, pairs of real numbers. For clarity, the name of the vector is kept, in this case u, in its coordinates, adding the subscript x or y to name its component in the x or y axis respectively

In V{displaystyle V;} the sum operation is defined:

+:V× × VΔ Δ V(u,v) w=u+v{displaystyle {begin{array}{ccll}+: stranger{Vtimes} {VV}{longrightarrow {}{longrightarrow {}{v}{v}{mathbf {u}mathbf {v}{v}{v}{mathbf}{w} =mathbf {v}{v}}}{mathbf}}{v}}{v}}}{mathbf}}{v}}{mathbf

where:

u=(ux,uand){displaystyle mathbf {u} =(u_{x},u_{y}}}

v=(vx,vand){displaystyle mathbf {v} =(v_{x},v_{y}}}

w=(wx,wand){displaystyle mathbf {w} =(w_{x},w_{y}}}

and the sum of u and v would be:

u+v=(ux,uand)+(vx,vand)=(ux+vx,uand+vand)=(wx,wand)=w{displaystyle mathbf {u} +mathbf {v} =(u_{x},u_{y})+(v_{x},v_{y})=(u_{x},u_{x},u_{y}+v_{y})=(w_{x},w_{y}

where:

wx=ux+vxwand=uand+vand{displaystyle {begin{array}{l}w_{x}=u_{x} +v_{x}w_{y}=u_{y}+v_{y}end{array}}}}}}}}

this implies that vector addition is internal and well defined.

The inner operation addition has the properties:

1) The commutative property, that is:

u+v=v+u,Русский Русский u,v한 한 V{displaystyle mathbf {u} +mathbf {v} =mathbf {v} +mathbf {u}quad forall {mathbf {u}mathbf {v} in {V}}

u+v=v+u{displaystyle mathbf {u} +mathbf {v} =mathbf {v} +mathbf {u} }

(ux,uand)+(vx,vand)=v+u{displaystyle (u_{x},u_{y})+(v_{x},v_{y})=mathbf {v} +mathbf {u} }

(ux+vx,uand+vand)=v+u{displaystyle (u_{x}+v_{x},u_{y}+v_{y})=mathbf {v} +mathbf {u} }

(vx+ux,vand+uand)=v+u{displaystyle (v_{x}+u_{x},v_{y}+u_{y})=mathbf {v} +mathbf {u} }

(vx,vand)+(ux,uand)=v+u{displaystyle (v_{x},v_{y})+(u_{x},u_{y})=mathbf {v} +mathbf {u} }

v+u=v+u{displaystyle mathbf {v} +mathbf {u} =mathbf {v} +mathbf {u} }

2) The associative property:

(u+v)+w=u+(v+w){displaystyle (mathbf {u} +mathbf {v})+mathbf {w} =mathbf {u} +(mathbf {v} +mathbf {w}}}}}

((ux,uand)+(vx,vand))+(wx,wand)=(ux,uand)+((vx,vand)+(wx,wand)){displaystyle {Big (}(u_{x},u_{y})+(v_{x},v_{y}){Big)}+(w_{x},w_{y})=(u_{x},u_{y}){Big(}(v_{x},v_{y}{w){x},

(ux+vx,uand+vand)+(wx,wand)=(ux,uand)+(vx+wx,vand+wand){displaystyle (u_{x}+v_{x},u_{y}+v_{y})+(w_{x},w_{y})=(u_{x},u_{y})+(v_{x},v_{x},v_{y}+w_{y});}

(ux+vx+wx,uand+vand+wand)=(ux+vx+wx,uand+vand+wand){displaystyle (u_{x}+v_{x}+w_{x},u_{y+v_{y}+w_{y})=(u_{x}+v_{x}},u_{x},u_{y}+v_{y}+w_{y});}

3) has neutral element 0{displaystyle mathbf {0} }:

u+0=u{displaystyle mathbf {u} +mathbf {0} =mathbf {u} }

(ux,uand)+(0,0)=(ux+0,uand+0)=(ux,uand){displaystyle (u_{x},u_{y})+(0,0)=(u_{x}+0,u_{y}+0)=(u_{x},u_{y});}

4) has opposite element:

u=(ux,uand){displaystyle mathbf {u} =(u_{x},u_{y}}}

− − u=(− − ux,− − uand){displaystyle mathbf {-u} =(-u_{x},-u_{y}}}}}}

u+(− − u)=(ux,uand)+(− − ux,− − uand)=(ux− − ux,uand− − uand)=(0,0)=0{displaystyle mathbf {u} +(mathbf {-u})=(u_{x},u_{y})+(-u_{x},-u_{y})=(u_{x}-u_{x},u_{y}-u_{y})=(0,0)=mathbf {0}}}}}

The operation product by a scalar:

⋅ ⋅ :K× × VΔ Δ V(a,u) v=a⋅ ⋅ u{displaystyle {begin{array}{ccll}cdot: fakeKtimes V fakelongrightarrow &V fake({mathit {a},mathbf {u}) strangermathbf} {v} ={mathit {a}}}cdot mathbf {u}{u end}{

The product of a and u will be:

a⋅ ⋅ u=a⋅ ⋅ (ux,uand)=(a⋅ ⋅ ux,a⋅ ⋅ uand)=(vx,vand)=v{displaystyle {mathit {a}}cdot mathbf {u} =acdot (u_{x},u_{y})=(acdot u_{x},acdot u_{y})=(v_{x},v_{y}}

where:

vx=a⋅ ⋅ uxvand=a⋅ ⋅ uand{displaystyle {begin{array}{l}v_{x}=acdot u_{x}v_{y}=acdot u_{y}end{array}}}}}}}}

this implies that vector-by-scalar multiplication is external and yet well defined.

5) has the associative property:

a⋅ ⋅ (b⋅ ⋅ u)=(a⋅ ⋅ b)⋅ ⋅ u,Русский Русский a,b한 한 K,Русский Русский u한 한 V{displaystyle {mathit {a}}cdot ({mathit {b}cdot mathbf {u})=({mathit {a}}{cdot {cdot} {b}}}{bdot mathbf {u}quad forall {cd}{cdot}{b }{b }, {b }{b }{b }{cdot}{b }}{b }{b }}{b }{b }{b }}{b }}{b }}{b }{b }{b }}}}{b }

This is:

a⋅ ⋅ (b⋅ ⋅ u)=(a⋅ ⋅ b)⋅ ⋅ u{displaystyle {mathit {a}}cdot ({mathit {b}cdot mathbf {u})=({mathit {a}}}cdot {mathit {b}})cdot mathbf {u} }

a⋅ ⋅ (b⋅ ⋅ (ux,uand))=(a⋅ ⋅ b)⋅ ⋅ (ux,uand){displaystyle {mathit {a}}cdot ({mathit {b}cdot (u_{x},u_{y}))=({mathit {a}}}}{cdot {mathit {b}}})cdot (u_{x},u_{y})}

a⋅ ⋅ (b⋅ ⋅ ux,b⋅ ⋅ uand)=(a⋅ ⋅ b)⋅ ⋅ (ux,uand){displaystyle {mathit {a}}cdot ({mathit {b}cdot u_{x},{mathit {b}}cdot u_{y})=({mathit {a}}}{cdot {mathit {b})cdot (u_{x},u_{y}}}}}}}

(a⋅ ⋅ b⋅ ⋅ ux,a⋅ ⋅ b⋅ ⋅ uand)=(a⋅ ⋅ b⋅ ⋅ ux,a⋅ ⋅ b⋅ ⋅ uand){cdot}{cdot}{cdot {b}{cdot u_{x},{mathit {a}}{cdot {mathit {b}{b}}{cdot u_{y}{cdot}{cdot}{cdot}{cdot}{cdot}{c}{cdot}{cdot}}{cdot}{cdot}{cdot}{c}}{c}{cdot}{cdot}{c}{cdot}{c

6) 1한 한 R{displaystyle {mathit {1}in {1}R} be neutral in the product:

1⋅ ⋅ u=u,Русский Русский u한 한 V{displaystyle {mathit {1}}cdot mathbf {u} =mathbf {u}quad forall {mathbf {u}{u}}

What results:

1⋅ ⋅ u=u{displaystyle {mathit {1}}cdot mathbf {u} =mathbf {u} }

1⋅ ⋅ (ux,uand)=u{displaystyle {mathit {1}}cdot (u_{x},u_{y}}}=mathbf {u} }

(1⋅ ⋅ ux,1⋅ ⋅ uand)=u{displaystyle ({mathit {1}}cdot u_{x},{mathit {1}}}cdot u_{y})=mathbf {u} }

(ux,uand)=u{displaystyle (u_{x},u_{y})=mathbf {u} }

That has the distributive property:

7) left distributive:

a⋅ ⋅ (u+v)=a⋅ ⋅ u+a⋅ ⋅ v,Русский Русский a한 한 R,Русский Русский u,v한 한 V{displaystyle {mathit {a}}cdot (mathbf {u} +mathbf {v}={mathit {a}}cdot mathbf {u} +{mathit {a}}}cdot mathbf {v}quad forall {cd}{bf}{bf}{

In this case we have:

a⋅ ⋅ (u+v)=a⋅ ⋅ u+a⋅ ⋅ v{displaystyle {mathit {a}}cdot (mathbf {u} +mathbf {v}={mathit {a}}cdot mathbf {u} +{mathit {a}}}cdot mathbf {v} }

a⋅ ⋅ ((ux,uand)+(vx,vand))=a⋅ ⋅ (ux,uand)+a⋅ ⋅ (vx,vand){displaystyle {mathit {a}}cdot ((u_{x},u_{y})+(v_{x},v_{y}))={mathit {a}}}{cdot (u_{x},u_{y})+{mathit {a}}cdot (v_{x},v_{y}{y}

a⋅ ⋅ (ux+vx,uand+vand)=(a⋅ ⋅ ux,a⋅ ⋅ uand)+(a⋅ ⋅ vx,a⋅ ⋅ vand){displaystyle {mathit {a}}cdot (u_{x}+v_{x},u_{y+v_{y})=({mathit {a}}{cdot u_{x},{mathit {a}}}{cdot u_{y}{cdot}{cdot v

a⋅ ⋅ (ux+vx,uand+vand)=(a⋅ ⋅ ux+a⋅ ⋅ vx,a⋅ ⋅ uand+a⋅ ⋅ vand){displaystyle {mathit {a}}cdot (u_{x}+v_{x},u_{y+v_{y})=({mathit {a}}}{cdot u_{x}}{mathit {a}}}{cdot v_{x},{cdot}{cdot u_{y

(a⋅ ⋅ (ux+vx),a⋅ ⋅ (uand+vand))=(a⋅ ⋅ (ux+vx),a⋅ ⋅ (uand+vand)){displaystyle ({mathit {a}cdot (u_{x}+v_{x}}),{mathit {a}cdot (u_{y}+v_{y})}{({mathit {a}}{cdot (u_{x}),{mathit {a}{cdot}{

8) right distributive:

(a+b)⋅ ⋅ u=a⋅ ⋅ u+b⋅ ⋅ u,Русский Русский a,b한 한 R,Русский Русский u한 한 V{displaystyle}{mathit {a} +{mathit {b}}})cdot mathbf {u} ={mathit {a}}cdot mathbf} {uthit {b}{bd}{bd}{bdot mathbf}{b }{b }{b }{b }{b }{b }{b }}{b }{b }{b }{b }}{b }}{b, }{b }}{b }{b }{b }{b }{b }{b }}}{b }{b }{b }{b }{b }}{b }{b, }{b }{b }{b }{b }}}}{b

Which in this case we have:

(a+b)⋅ ⋅ u=a⋅ ⋅ u+b⋅ ⋅ u{displaystyle ({mathit {a}}+{mathit {b}})cdot mathbf {u} ={mathit {a}}cdot mathbf {u} +{mathit {b}}}cdot mathbf {u}}}

(a+b)⋅ ⋅ (ux,uand)=a⋅ ⋅ (ux,uand)+b⋅ ⋅ (ux,uand){displaystyle ({mathit {a} +{mathit {b}}})cdot (u_{x},u_{y})={mathit {a}}}cdot (u_{x},u_{y})+{mathit {b}cdot (u_{x},u_{y}}}}}}}}}}}}}}

(a+b)⋅ ⋅ (ux,uand)=(a⋅ ⋅ ux,a⋅ ⋅ uand)+(b⋅ ⋅ ux,b⋅ ⋅ uand){displaystyle ({mathit {a}+{mathit {b}})cdot (u_{x},u_{y})=({mathit {a}}{cdot u_{x},{mathit {a}}}{cdot u_{y}{cdot}{cdot u_

(a+b)⋅ ⋅ (ux,uand)=(a⋅ ⋅ ux+b⋅ ⋅ ux,a⋅ ⋅ uand+b⋅ ⋅ uand){displaystyle ({mathit {a} +{mathit {b}}})cdot (u_{x},u_{y})=({mathit {a}}{cdot u_{x}}{b}{mathit {b}{b}{b }{b }{b }{b }{b }{b }{b }{b }{b }{b }{b }{b

((a+b)⋅ ⋅ ux,(a+b)⋅ ⋅ uand)=((a+b)⋅ ⋅ ux,(a+b)⋅ ⋅ uand){displaystyle({mathit {a}+{mathit {b}}})cdot u_{x},({mathit {a}}+{mathit {b}}{cdot u_{y}{y}{cdot u_{y}{cd}{cd}{cd}{cd}{cd}{cd}{cdot}{cd}{cd}}{cd}{cdot}{cd}{cd}{cd }{cd }{cd }{b }{cd }{cd }{cd }{cd }{cd }{cd }{cd }{

It is shown that it is a vector space.

Examples

The bodies

Every field is a vector space over itself, using the product of the field as a scalar product.

• C{displaystyle mathbb {C} } is a dimension one vector space C{displaystyle mathbb {C} }.

• C{displaystyle mathbb {C} } It's a vector space over R{displaystyle mathbb {R} }.
• C{displaystyle mathbb {C} } It's a vector space over Q{displaystyle mathbb {Q} }.

Sequences over a field K

The best known vector space noted as Kn{displaystyle K_{}^{n}}Where n0 is an integer, has as elements n-tuplas, that is, finite successions of K{displaystyle K_{}^{}{}}} length n operations:

(u₁, u₂,... u_n)+(v₁, v₂,... v_n♪u₁+v₁, u₂+v₂,... u_n+v_n).

a(u₁, u₂,... u_n♪au₁, au₂,... au_n).

The infinite successions of K{displaystyle K^{} are vectorial spaces with operations:

(u₁, u₂,... u_n,...)+(v₁, v₂,... v_n,...)=(u₁+v₁, u₂+v₂,... u_n+v_n...).

a(u₁, u₂,... u_n,...)=(au₁, au₂,... au_n...).

The space of the matrices n× × m{displaystyle ntimes m}, Mn× × m(K){displaystyle M_{ntimes m}(K)}About K{displaystyle K^{}with operations:

(x1,1 x1,m xn,1 xn,m)+(and1,1 and1,m andn,1 andn,m)=(x1,1+and1,1 x1,m+and1,m xn,1+andn,1 xn,m+andn,m)##### ###########################################################################################################################################################################################################################################################

a(x1,1 x1,m xn,1 xn,m)=(ax1,1 ax1,m axn,1 axn,m){displaystyle a{begin{pmatrix}x_{1,1}{cdots > }{1,mvdots > ultimatevdots \xx_{n,1}{n,1}{nx}{nx}{n, i mean, i'm}{n, i mean, i'm}{n, i mean, i mean, i mean, i don't.

Also vectorial spaces are any grouping of elements of K{displaystyle K_{}^{}{}}} in which the sum and product operations are defined between these groups, element to element, similar to that of matrices n× × m{displaystyle ntimes m}, so for example we have the boxes n× × m× × r{displaystyle ntimes mtimes r} on K{displaystyle K_{}^{}{}}} which appear in the development of Taylor in order 3 of a generic function.

Application spaces over a body

The whole F{displaystyle F_{}^{}{}}} applications f:M→ → K{displaystyle f:Mrightarrow K}, K{displaystyle K^{} a body and M{displaystyle M_{}^{}{}} a set, they also form vector spaces through the sum and the usual multiplication:

Русский Русский f,g한 한 F,Русский Русский a한 한 K{displaystyle forall f,gin F,;forall ain K}

(f+g)(w):=f(w)+g(w),(af)(w):=a(f)(w).{displaystyle {begin{matrix}(f+g)(w) alien:=f(w)+g(w)_{{},\;;;;;(af)(w)(w)(f)(w)(w)_{}{^{}{}.;;;;;;;;;;;

Polynomials

Amount of f(x)=x+x² and g(x)=-x².

The vector space K[chuckles]x]{displaystyle K[x]} formed by polynomial functions, let's see:

General expression: p(x)=rnxn+rn− − 1xn− − 1+...+r1x+r0{displaystyle p(x)=r_{n}x^{n}+r_{n-1}x_{n-1}{n-1}{n-1}+r_{1}x+r_{0}}}}}Where rn,...,r0한 한 K{displaystyle r_{n},;...r_{0}in K}Consider it. n;r_{i}=0}" xmlns="http://www.w3.org/1998/Math/MathML">Русский Русский i▪nri=0{displaystyle forall i rigidn;r_{i}=0}n;r_{i}=0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b58bde634187f988fe6e7b0f7edce560e43ed2" style="vertical-align: -0.671ex; width:13.343ex; height:2.509ex;"/>.

p(x)+q(x)=(rnxn+rn− − 1xn− − 1+...+r1x+r0){displaystyle p(x)+q(x)=(r_{n}x^{n}+r_{n-1}x^{n-1}+...+r_{1}x+r_{0}{0}{}}}} +(smxm+sm− − 1xm− − 1+...+s1x+s0){displaystyle +(s_{m}x^{m}+s_{m-1}x^{m-1+}...+s_{1}x+s_{0}^{}{s}}}}}} =...{displaystyle} =(tMxM+tM− − 1xM− − 1+...+t1x+t0)=(p+q)(x){displaystyle =(t_{M}x^{M}+t_{M-1}x^{M-1+}...+t_{1}x+t_{0}^{}{}(p+q)(x)}}Where M=max{m,n!{displaystyle M=max{m,;n}_{}{}{^{} and ti=ri+si{displaystyle t_{i}=r_{i}+s_{i}^{i}{i}},

a(p(x))=a(rnxn+rn− − 1xn− − 1+...+r1x+r0){displaystyle a(p(x))=a(r_{n}x^{n}+r_{n-1}x^{n-1}+...+r_{1}x+r_{0}^{}{})} =(arnxn+arn− − 1xn− − 1+...+ar1x+ar0){displaystyle =(ar_{n}x^{n}+ar_{n-1}x^{n-1+}...+ar_{1}x+ar_{0}{0}^{}{}}} =tnxn+tn− − 1xn− − 1+...+t1x+t0=(ap)(x){displaystyle =t_{n}x^{n}+t_{n-1}x^{n-1}+t_{1}x+t_{0}^{}=(ap)(x)}}.

Power series are similar, except that infinitely many nonzero terms are allowed.

Trigonometric functions

Trigonometric functions form vector spaces with the following operations:

General expression: f(x)=af␡ ␡ i=1n(bf,isen(ix)+cf,i# (ix))한 한 L2{displaystyle f(x)=a_{f}^{}sum _{i=1}^{n}(b_{f,i}{mbox{sen}}}(ix)+c_{f,i}cos(ix)}in L^{2}}}}

(f+g)(x):=f(x)+g(x){displaystyle (f+g)(x):=f(x)+g(x)_{}^{}}} =af␡ ␡ i=1n(bf,isen(ix)+cf,i# (ix))+ag␡ ␡ i=1n(bg,isen(ix)+cg,i# (ix)){displaystyle =a_{f}sum _{i=1}^{n}(b_{f,i}{mbox{sen}}}(ix)+c_{f,i}cos(ix)))+a_{g}sum _{i=1^}{n}(b_{g,i}{mbox{sen}(ix)+c_cos{g,} =(af+ag)␡ ␡ i=1n((bf,i+bg,i)sen(ix)+(cf,i+cg,i)# (ix))한 한 L2{displaystyle =(a_{f}+a_{g})sum _{i=1}^{n}(b_{f,i}+b_{g,i}){mbox{sen}}}(ix)+(c_{f,i}+c_{g,i})cos(ix)in L^{2}}}},

(af)(x):=af(x){displaystyle (af)(x):=af(x)_{}^{}} =a(af␡ ␡ i=1n(bf,isen(ix)+cf,i# (ix))){displaystyle =a_{f}sum _{i=1}{n}(b_{f,i}{mbox{sen}}}(ix)+c_{f,i}cos(ix))}}} =aaf␡ ␡ i=1n(abf,isen(ix)+acf,i# (ix))한 한 L2{displaystyle =aaa_{f}sum _{i=1}{n}(ab_{f,i}{mbox{sen}}}(ix)+ac_{f,i}cos(ix))in L^{2}}.

Systems of linear homogeneous equations

System of 2 equations and 3 variables

{a1,1x1+...... +a1,nxn=0 am,1x1+...... +am,nxn=0{displaystyle {begin{cases}{begin{matrix}a_{1,1x_{1}{1}{1}{1}{1,n}x_{n}{n}{n}{0vdots " #vdots " {vdots \a_{m,1}{1}{1}{1}{1}{1}{1}{1}{1⁄2}{x}{1⁄2⁄2}{dox1}{x}{nx}{nx}{nx or equivalent (a1,1+...... +a1,n am,1+...... +am,n)(x1 xn)=(0 0){dotsplaystyle {begin{pmatrix}a_{1,1}{dots > }{1,nvdots &vdots &vdots '{a_{m,1}{dots > {m, n}{pmatrix}{bs}{x#x simplified as Ax=0{displaystyle A_{}{}x=0}

A homogeneous linear equation system (linear sequences in which x=0{displaystyle x=0_{}{}{}{}{}} is always a solution, that is, (x1,...... ,xn)=(0,...... ,0){displaystyle (x_{1},;dots;x_{n})=(0,dots;0)}) has solutions that form a vector space, can be seen in its two operations:

Yeah. Ax=0,Aand=0⇒ ⇒ Ax+Aand=0⇒ ⇒ {displaystyle Ax=0,Ay=0Rightarrow Ax+Ay=0Rightarrow } A(x+and)=0{displaystyle A(x+y)=0_{}^{}{}

Yeah. Ax=0,a한 한 K⇒ ⇒ a(Ax)=0⇒ ⇒ {displaystyle Ax=0,ain KRightarrow a(Ax)=0Rightarrow } A(ax)=0{displaystyle A(ax)=0_{}^{}}.

Also that equations themselves, rows of the matrix A{displaystyle A_{}^{}{}}} notated as a matrix 1× × n{displaystyle 1times n}I mean, Ei=(ai,1,...... ,ai,n){displaystyle E_{i}=(a_{i,1},;dots;a_{i,n}}}}, they are a vector space, as you can see in your two operations:

Yeah. Eix=0,Ejx=0⇒ ⇒ {displaystyle E_{i}x=0,;e_{j}x=0Rightarrow } Eix+Ejx=0⇒ ⇒ (Ei+Ej)x=0{displaystyle E_{i}{}x+e_{j}x=0Rightarrow (E_{i}+E_{j})x=0}

Yeah. Eix=0,a한 한 K⇒ ⇒ {displaystyle E_{i}x=0,;ain KRightarrow } a(Eix)=0⇒ ⇒ (aEi)x=0{displaystyle a(E_{i}^{}x.

Vector subspace

Definition

Sea V{displaystyle V} a vectorial space K{displaystyle K} and U V{displaystyle Usubseq V} a non-empty subset V{displaystyle V}It's said that U{displaystyle U} is a vector subspace V{displaystyle V} Yes:

1. u+v한 한 U{displaystyle u+vin U}
2. β β u한 한 U{displaystyle beta uin U}

Русский Русский u,v한 한 U{displaystyle forall ;u,vin U} and β β 한 한 K{displaystyle beta in K}.

Consequences

U{displaystyle U} inherits the operations of V{displaystyle V} as well-defined applications, i.e. they do not escape U{displaystyle U}and as a consequence we have to U{displaystyle U} It's a vector space over K{displaystyle K}.

With any subset of elements selected in the previous vector spaces, not empty, vector subspaces can be generated, for this it would be useful to introduce new concepts that will facilitate the work on these new vector spaces.

Internal results

To detail the internal behavior of all vector spaces in a general way, it is necessary to expose a series of tools chronologically linked to each other, with which it is possible to construct valid results in any structure that is a vector space.

Linear Combination

Each vector u is a unique linear combination

Given a vector space E{displaystyle E_{}^{}{}}We'll say a vector u한 한 E{displaystyle uin E} That's it. linear combination of vectors S={v1,...... ,vn! E{displaystyle S={v_{1},dotsv_{n}subseq E} if they exist a1,...... ,an한 한 R{displaystyle a_{1},dotsa_{n}in mathbb {R} } such that

u=a1v1+ +anvn{displaystyle u=a_{1}v_{1}+cdots +a_{n}v_{n}}

We'll denote how S E{displaystyle langle S_{}^{}{rangle _{E}}} the resulting set of all linear combinations of vectors S E{displaystyle S_{}{}subset E}.

Proposition 1

Done E{displaystyle E_{}^{}{}} a vectorial space S E{displaystyle Ssubset E_{}^{}} a set of vectors, the set F= S E{displaystyle F=langle S_{}^{}rangle _{E}} is the smallest vectorial subspace contained in E{displaystyle E_{}^{}{}} and containing a S{displaystyle S_{}^{}{}}.

Note. In this case it is said that S{displaystyle S_{}^{}{}} It's a generator system that generates F{displaystyle F_{}^{}{}}}.

Linear independence

We'll say a set S={v1,...... ,vn!{displaystyle S_{}^{}={v_{1},;dots;v_{n}}}} of vectors is linearly independent if vector 0 cannot be expressed as a non-nul linear combination of vectors S{displaystyle S_{}^{}{}}I mean,

Yeah. 0=a1v1+ +anvn⇒ ⇒ a1= =an=0{displaystyle 0=a_{1}v_{1}+cdots +a_{nv_{n}{n}Rightarrow a_{1}=cdots =a_{n}=0}.

We'll say a set S{displaystyle S_{}^{}{}} of vectors is linearly dependent if it's not linearly independent.

Proposition 2

v1,...... ,vn{displaystyle v_{1},;dots;v_{n}} are linearly dependent Δ Δ consuming consuming viI was. I was. 0:vi=␡ ␡ iI was. I was. j≥ ≥ 1najvj{displaystyle Leftrightarrow exists v_{i}neq 0:v_{i}=sum _{ineq jgeq 1}^{n}a_{j}v_{j}}}

Basis of a vector space

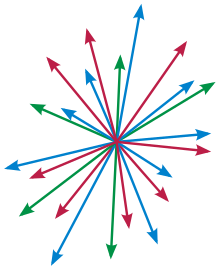
The bases reveal the structure of vector spaces in a concise way. A basis is the smallest set (finite or infinite) B = {v_i}_{i ∈ I} of vectors spanning the entire space. This means that any vector v can be expressed as a sum (called a linear combination) of elements of the basis

a₁v_i1 + a₂v_i2 +... + a_nv_in,

where the a_ks are scalars and v_{i k} (k = 1,..., n) elements of base B. Minimality, on the other hand, is made formal by the concept of linear independence. A set of vectors is said to be linearly independent if none of its elements can be expressed as a linear combination of the others. Equivalently, an equation

a₁v_i1 + a_i2v₂ +... + a_nv_in = 0

only achieved if all scalars a₁,..., a_n are equal to zero. By definition of the basis each vector can be expressed as a finite sum of the elements of the basis. Due to linear independence this type of representation is unique. Vector spaces are sometimes introduced from this point of view.

Basis formally

v₁ and v₂ they are the basis of a plane, if there were linear dependence (aligned), the grid could not be generated.

Given a system of generators, we say that it is a basis if they are linearly independent.

Proposition 3. Given a vector space E,{v1,...... ,vn!=F E{displaystyle E,;{v_{1},;dotsv_{n}=Fsubset E} It's a base. Δ Δ {displaystyle Leftrightarrow } Русский Русский u한 한 E,consuming consuming !ai한 한 K,i한 한 1,...... ,n:{displaystyle forall uin E,;exists !a_{i}in K,;iin {1,dotsn}:} u=␡ ␡ i=1naivi{displaystyle u=sum _{i=1}{n}a.

Proposal 4. Given a vector space E,S={v1,...... ,vn!{displaystyle E,;S={v_{1},;dots;v_{n}}}} linearly independent and u S ⇒ ⇒ {displaystyle unotin langle Srangle Rightarrow } {u! S={u,v1,...... ,vn!{displaystyle {u}cup S={u,;v_{1},;dots;v_{n}} They are linearly independent.

Generator Base Theorem

Every system of generators has a base.

Steinitz Theorem

Every basis of a vector space can be partially changed by linearly independent vectors.

Corolary. If a vector space E{displaystyle E_{}^{}{}} has a base n{displaystyle n_{}^{}{}}} vectors ⇒ ⇒ {displaystyle Rightarrow } any other base has n{displaystyle n_{}^{}{}}} vectors.

Observation

Every vector space has a basis. This fact is based on Zorn's lemma, an equivalent formulation of the axiom of choice. Given the other axioms of Zermelo-Fraenkel set theory, the existence of bases is equivalent to the axiom of choice. The ultrafilter lemma, which is weaker than the axiom of choice, implies that all bases of a vector space have the same "size", that is, cardinality. If the space is generated by a finite number of vectors, all of the above can be demonstrated without the need to resort to set theory.

Dimension

Given a vectorial space K{displaystyle K_{}^{}{}}}:

• If you have a finite base, we'll say dimension to the number of elements of that base.
• If you have no finite base, we'll say it's from infinite dimension.

Notation

Given a vector space E{displaystyle E_{}^{}{}} and a subspace F E{displaystyle F_{}^{}subset E}We have to:

• Yeah. E{displaystyle E_{}^{}{}} dimension n{displaystyle n_{}^{}{}}} We will indicate it as dim (E)=n{displaystyle dim(E)=n_{}^{}.
• Yeah. F{displaystyle F_{}^{}{}}} dimension m{displaystyle m_{}^{}{}}} as subspace E{displaystyle E_{}^{}{}} We will indicate it as dimE (F)=m{displaystyle dim _{E}(F)=m_{}^{}}}.

Intersection of vector subspaces

Given two vector subspaces F,G E{displaystyle F,Gsubset E}, intersection is vectorial subspace contained in these and we will note it as:

F G:={u:u한 한 F,u한 한 G!{displaystyle Fcap G:={u:;uin F,;uin G}}.

Comments. For the successive intersection of vectorial spaces it is inductively derived from two in two.

The union of vector subspaces is not in general a vector subspace.

Sum of vector subspaces

Given two vector subspaces F,G E{displaystyle F,Gsubset E}, the sum is a vector subspace that contains these and we will note it as:

F+G:={u=v1+v2:v1한 한 F,v2한 한 G!{displaystyle F+G:={u=v_{1}+v_{2}:;v_{1}in F,;v_{2}in G}}}}.

If F and G are vector subspaces of E, their sum F+G is the smallest vector subspace of E that contains both F and G.

Observation. For the successive sum of vectorial spaces it is inductively derived from two in two.

Grassmann's Formula Theorem

Given two vector subspaces F,G E{displaystyle F,Gsubset E} of finite dimension, we have the following result:

dimE (F+G)=dimE (F)+dimE (G)− − dimE (F G){displaystyle dim _{E}(F+G)=dim _{E}(F)+dim _{E}(G)-dim _{E}(Fcap G)}}}.

Direct sum of vector subspaces

Given two vector subspaces F,G E{displaystyle F,Gsubset E}We'll say F+G{displaystyle F+G_{}{}{}{}} It's a Direct Yeah. F G=0{displaystyle Fcap G={0} and we will denote it as:

F G{displaystyle Foplus G}.

When F{displaystyle F} and G{displaystyle G} are in direct sum, each vector F+G{displaystyle F+G} is expressed uniquely as a sum of a vector F{displaystyle F} and another vector G{displaystyle G}.

Quotient of vector spaces

Given a vector space E{displaystyle E,} and a vector subspace F E{displaystyle Fsubset E}.

Dice u,v한 한 E{displaystyle u,vin E} We'll say they're related module. F{displaystyle F,} Yeah. u− − v한 한 F{displaystyle u-vin F}.

• The previous relationship is an equivalence relationship.

Note by [chuckles]u]=u+F:={u+v:v한 한 F!{displaystyle [u]=u+F:={u+v:vin F}} ={w:w=u+v,v한 한 F!{displaystyle ={w:w=u+v,;vin F}} to class u{displaystyle u,} module F{displaystyle F,}.

We will call the set of equivalence classes above quotient set or quotient space:

Note by E/F{displaystyle E/F_{}{}{}{}} to that quotient space.

Space E/F{displaystyle E/F_{}{}{}{}} is a vector space with the following operations:

[chuckles]u]+[chuckles]v]:=[chuckles]u+v]λ λ [chuckles]u]:=[chuckles]λ λ u]{displaystyle {begin{matrix}[u]+[v] alien:= fake[u+v];;;;;;;;;lambda [u] fantasy:= stranger[lambda u];;;;end{matrix}}}}}

Basic Constructions

In addition to what was exposed in the previous examples, there are a series of constructions that provide us with vector spaces from others. In addition to the concrete definitions below, they are also characterized by universal properties, which determine an object X by specifying the linear maps of X to any other vector space.

Direct addition of vector spaces

Given two vectorial spaces E,F{displaystyle E,;F_{}^{}} on the same body K{displaystyle K_{}^{}{}}}, we'll call a direct sum to the vector space E× × F={displaystyle Etimes F=}{u:=(u1,u2):u1한 한 E,u2한 한 F!{displaystyle {u:=(u_{1},;u_{2}):u_{1}in E,;u_{2}in F}}}Let's see that the two operations are well defined:

u+v=(u1,u2)+(v1,v2)={displaystyle u+v=(u_{1},;u_{2})+(v_{1},;v_{2})=}(u1+v1,u2+v2){displaystyle (u_{1}+v_{1},;u_{2}+v_{2}}}}},

au=a(u1,u2)={displaystyle au=a(u_{1},;u_{2})=}(au1,au2){displaystyle (au_{1},;au_{2}}}}.

Vector spaces with additional structure

From the point of view of linear algebra, vector spaces are fully understood insofar as any vector space is characterized, except for isomorphisms, by its dimension. However, ad hoc vector spaces do not offer a framework to address the fundamental question for the analysis of whether a sequence of functions converges to another function. Also, linear algebra is not adapted per se to deal with infinite series, since addition only allows a finite number of terms to be added. The needs of functional analysis require considering new structures.

Norminated spaces

A vector space is normed if it is endowed with a norm.

Proposed 5. A standard space is a metric space, where the distance is given by:

d(x,and)= x− − and {displaystyle d(x,y)=associatedx-yassociated}

Every distance induced by the norm is a distance.

Topological Vector Spaces

Given a topology Δ Δ {displaystyle tau _{}{}{displaystyle tau} about a vector space X{displaystyle X_{}^{}{}}} where the points are closed and the two operations of the vector space are continuous with respect to those topology, we will say that:

• Δ Δ {displaystyle tau _{}{}{displaystyle tau} It's a vectorial topology on X{displaystyle X_{}^{}{}}},
• X{displaystyle X_{}^{}{}}} It's a vectorial topological space.

Proposition 6.. All topological vector space endowed with a metric is standard space.

Proposal 7.. All standard space is a topological vector space.

Banach spaces

A Banach space is a normed and complete space.

Prehilbertian spaces

A prehilbertian space It's a pair. (E, ⋅ ⋅ 日本語⋅ ⋅ ){displaystyle (E_{}{},langle cdot Δcdot rangle)}Where E{displaystyle E_{}^{}{}} It's a vector space. ⋅ ⋅ 日本語⋅ ⋅ {displaystyle langle cdot ⋅cdot rangle } is a product to scale.

Hilbert spaces

A Hilbert space is a pre-Hilbert space complete by the norm defined by the scalar product.

Morphisms between vector spaces

They are applications between vector spaces that maintain the structure of vector spaces, that is, they preserve the two operations and their properties from one to another of these spaces.

Linear maps

Given two vectorial spaces E{displaystyle E_{}^{}{}} and F{displaystyle F_{}^{}{}}}on the same body, we will say that an application f:E→ → F{displaystyle f:Erightarrow F} That's it. linear Yes:

f(u+Ev)=f(u)+Ff(v){displaystyle f(u+_{E}v)=f(u)+_{F}f(v)_{}{}{}{}{},

f(a⋅ ⋅ Eu)=a⋅ ⋅ Ff(u){displaystyle f(acdot _{E}u)=acdot _{F}f(u)}.