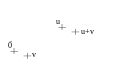Vector subspace

In linear algebra, a vector subspace is the subset of a vector space, which by itself satisfies the definition of a vector space with the same operations as V the original vector space.

Definition of a vector subspace

Sea V{displaystyle V_{}^{}{}}} a vectorial space K{displaystyle K_{}^{}{}}} and U V{displaystyle Usubset V} not empty, U{displaystyle U_{}^{}{}}} It's a vector subspace of V{displaystyle V_{}^{}{}}} Yes:

i)Русский Русский u,v한 한 U,u+v한 한 U{displaystyle i);forall u,vin U,u+vin U}

ii)Русский Русский u한 한 U,Русский Русский k한 한 K,ku한 한 U{displaystyle ii);forall uin U,forall kin K,kuin U}

Consequences

• A subset of vectors that meets the two previous conditions is a vector subspace and therefore a vector space.

Notations

Done F{displaystyle F,} a vector subspace, you have:

To (i) abuse of language F+F F{displaystyle F+Fsubset F}and even F+F=F{displaystyle F+F=F} That's right.

Demonstration

You want to see that Русский Русский w한 한 F+FΔ Δ w한 한 F{displaystyle forall win F+FLeftrightarrow win F}: ⇒ ⇒ )w한 한 F+F⇒ ⇒ consuming consuming u,v한 한 F:w=u+v⇒ ⇒ w한 한 F.{displaystyle Rightarrow)win F+FRightarrow exists u,vin F:w=u+vRightarrow win F.}   )w한 한 F⇒ ⇒ w=w+0→ → ⇒ ⇒ w한 한 F+F{displaystyle Leftarrow)win FRightarrow w=w+{vec {0}}Rightarrow win F+F}

(ii) abuse of language λ λ F F{displaystyle lambda Fsubset F}and even λ λ F=F,Русский Русский λ λ 한 한 K− − {0!{displaystyle lambda F=F,;forall lambda in K-{0}} That's right.

Demonstration

w한 한 FΔ Δ 1λ λ w한 한 FΔ Δ λ λ 1λ λ w한 한 λ λ FΔ Δ w한 한 λ λ F{displaystyle win FLeftrightarrow {frac {1}{lambda }w}in FLeftrightarrow lambda {frac {1}{lambda }}win lambda FLeftrightarrow win lambda F}

Verification criteria

It is possible to synthesize i) and ii) in a single condition:

Examples

Given the vector space R2{displaystyle mathbb {R} ^{2}}, its elements are the type (a,b)한 한 R2{displaystyle (a,b)in mathbb {R} ^{2}}.

• 

  0→ → ,u{displaystyle {vec {0},u} and λ λ u{displaystyle lambda u} They're aligned, Русский Русский u한 한 R2{displaystyle forall uin mathbb {R} ^{2}}, Русский Русский λ λ 한 한 K.{displaystyle forall lambda in K.}

• 

  0→ → ,u,v{displaystyle {vec {0},u,v} and u+v{displaystyle u+v} form a parallelogram if they are not aligned, Русский Русский u,v한 한 R2.{displaystyle forall u,vin mathbb {R} ^{2}. !

• 

  Amount of 3 elements.

The subset

U={(a,b):a+b=0!{displaystyle U={(a,b):a+b=0}.

is a vector subspace.

Demonstration

By definition of U the elements are of the form x=(x1,− − x1){displaystyle x=(x_{1},-x_{1})}. Suma+:R2× × R2Δ Δ R2(u,v) (u1,− − u1)+(v1,− − v1)=((u1+v1),− − (u1+v1)){display} {begin{matrix}Suma style+: stranger{mathbb} {R ^{2}{2}mathbb {R} ^{2}{2}{longrightarrow}{mathbb} {R}{2}{2}{2}{mathbf {u}{1mathbf}}{ Prorductor⋅ ⋅ :K× × VΔ Δ V(a,u) a⋅ ⋅ (u1,− − u1)=((a⋅ ⋅ u1),− − (a⋅ ⋅ u1)){displaystyle {begin{matrix}Producto fakecdot {}: fake{Ktimes {}V}{longrightarrow {}{longrightarrow {}{v}{pos(a,mathbf {u}}{a}{mathbf}{amapsto &acdot}{u_{1}{1}{1}{1}{cdot}}{cdot}{cdot}}{cdot}}{cdot}{cdot}{cdot}}{cdot as operations are well defined then U is in itself a vectorial space, that is, satisfying the conditions of vector subspace R2{displaystyle mathbb {R} ^{2}}.

The subset

C={(a,b):b=a2!{displaystyle C={(a,b):b=a^{2}}}}

is not a vector subspace.

Operations with subspaces

Sea (V,+,K,↓ ↓ ){displaystyle (V,+,K,*)} a vector space; (S,+,K,↓ ↓ ){displaystyle (S,+,K,*)} and (W,+,K,↓ ↓ ){displaystyle (W,+,K,*)} vectorial subspaces V{displaystyle V}the following operations are defined:

Union

S W={v한 한 V:: v한 한 Sorv한 한 W!{displaystyle Scup W=left{mathbf {v} in Vcolon mathbf {v}in S {text{o}mathbf {v} in Wright}}}}
In general, the union of subspaces is not a subspace.

Intersection

S W={v한 한 V:: v한 한 Sandv한 한 W!{displaystyle Scap W=left{mathbf {v} in Vcolon mathbf {v} in S {text{y}mathbf {v} in Wright}}}}}
The intersection of two subspaces is a subspace.

Sum

S+W={v한 한 V:: v=(u1+u2)∧ ∧ u1한 한 S∧ ∧ u2한 한 W!{displaystyle S+W=left{mathbf {v} in Vcolon mathbf {v} =(mathbf {u_{1}} +mathbf {u_{2}}}})wedge mathbf {u_{u_{1}}wedge swedge mathbf {u_{u_{u_right}}}}{u_{u_{u_{wright}}}}
The sum of two subspaces is a subspace V.

Direct addition

If the intersection between S and W is the trivial subspace (i.e., the null vector), then the sum is called "direct sum".
I mean, yeah. S W={0→ → !⇒ ⇒ S W{displaystyle Scap W=left{vec {0}right}Rightarrow Soplus W}
This means all vectors S+W, it is written in a way unique as the sum of a vector S and another W.

Supplementary Subspaces

It is said that the subspaces S{displaystyle S} and W{displaystyle W}They are. Supplementary when they verify that their direct sum is equal to the vector space V{displaystyle V}:

S W=V▪ ▪ {S+W=VS W={0→ → !{displaystyle Soplus W=;V;leftrightarrow ;{begin{cases}S+W=;VScap W=leftlbrace {overset {rightarrow }{0}{0}{rightrbrace end{cases}}}}}

Dimensions of subspaces

Grassmann's formula resolves that the sum dimension of subspaces S{displaystyle S} and W{displaystyle W} will be equal to the dimension of subspace S{displaystyle S} plus the subspace dimension W{displaystyle W} less the dimension of the intersection of both, i.e.:

dim (S+W)=dim (S)+dim (W)− − dim (S W){displaystyle dim(S+W)=dim(S)+dim(W)-dim(Scap W)}

For example, being dim (S)=3{displaystyle dim(S)=3} and dim (W)=2{displaystyle dim(W)=2} and having as intersection a subspace dimension 1.
Then, dim (S+W)=4{displaystyle dim(S+W)=4}.

In direct addition

In the particular case of the direct sum, as S W={0→ → !⇒ ⇒ dim (S W)=0{displaystyle Scap W=left{vec {0}}right}Rightarrow dim(Scap W)=0}.
Grassmann's formula is:

dim (S W)=dim (S)+dim (W){displaystyle dim(Soplus W)=dim(S)+dim(W)}

Then in the previous example, it would be dim (S W)=5{displaystyle dim(Soplus W)=5}.