Universal quantizer

In logic, the symbol is used Русский Русский {displaystyle forall }, called universal quantificationa variable to say that "for everything" element of a certain set is fulfilled the proposition given below.

Русский Русский x한 한 B{displaystyle forall xin B}

Example

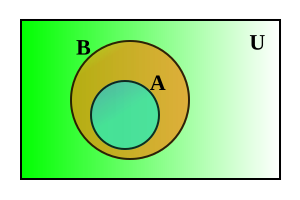
If we have two different sets A and B, and A is a subset of B:

A B∧ ∧ AI was. I was. B∧ ∧ AI was. I was. ∅ ∅ {displaystyle Asubset B;land ;Aneq B;land ;Aneq varnothing }

Every element x of A belongs to B:

Русский Русский x한 한 A⇒ ⇒ x한 한 B{displaystyle forall xin A;Rightarrow ;xin B}

Since A and B are different sets as indicated in the diagram, we can say that not all elements and of B belong to A, this being a sufficient guarantee that two sets can be different:

¬ ¬ Русский Русский and한 한 B:and한 한 A{displaystyle lnot forall yin B:;yin A,}

That is: not for every element y of B it is true that y also belongs to A.

Relation universal quantifier and existential quantifier

Given an expression P(x), according to the universal quantifier it can be transformed into another equivalent one with the existential quantifier:

Русский Русский xP(x)Δ Δ ¬ ¬ consuming consuming x¬ ¬ P(x){displaystyle forall x P(x);Leftrightarrow ;lnot exists x lnot P(x),}

that we could read: if for all x P(x) holds, there is no x that does not hold P(x).

Based on the example above:

Русский Русский x한 한 A:x한 한 B{displaystyle forall xin A:;xin B,}

For every x that belongs to A, it is true that x belongs to B. What can we express:

¬ ¬ consuming consuming x한 한 A:x B{displaystyle lnot exists xin A:;xnotin B,}

There is no x of A, which satisfies that x is not in B.