Tunnel effect

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Reflection and "tune" of an electron aimed at a potential barrier. The glowing point moving from right to left is the reflected section of the wave pack. A glimpse can be seen at the right of the barrier. This small fraction of the wave pack crosses the tunnel in an impossible way for classic systems. The interference of the contours between emission and reflection waves is also remarkable.

In quantum mechanics, the tunneling effect is a quantum phenomenon whereby a particle violates the principles of classical mechanics by penetrating a barrier of potential or impedance greater than the kinetic energy of the particle itself. A barrier, in quantum terms applied to tunneling, is a quality of the energetic state of matter analogous to a "hill"; or classic slope, composed of alternating crests and flanks, which suggests that the shortest path of a mobile between two or more flanks must cross its corresponding intermediate crest. If the object does not have enough mechanical energy to pass through the barrier, classical mechanics states that it can never appear in a state belonging to the other side of the barrier.

At the quantum scale, objects exhibit wavelike behavior; in quantum theory, a quantum moving in the direction of a "hill" The potentially energetic can be described by its wave function, which represents the probable amplitude of the particle if found in the position beyond the structure of the curve. If this function describes the position of the particle belonging to the flank adjacent to the one it assumed its starting point, there is a certain probability that it has moved "through" of the structure, instead of overcoming it by the conventional route that crosses the relative energetic peak. This is known as the tunnel effect.

The tunneling effect plays an essential role in many physical phenomena, such as the nuclear fusion that occurs in the main sequence of stars like the Sun. The energy possessed by the hydrons (hydrogen cation) in the core of the Sol is not enough to overcome the potential barrier that produces the electromagnetic repulsion between them. Thanks to the tunneling effect, there is a small probability that some hydrons will pass it, causing the fusion of the same and releasing energy in the form of electromagnetic radiation. Although the probability of this tunneling effect is very small, the immense amount of particles that make up the Sun causes this effect to occur constantly. This explains why the more massive a star (such as a blue supergiant) is, the shorter its main sequence, since the kinetic energy of hydrons is higher and consequently the tunneling probability is higher.

History

In about 1928, George Gamow solved the theory of Alpha decay of atomic nuclei through tunneling properties. Classically, the particle is confined to the nucleus due to the enormous amount of energy required to escape its potential. Similarly, an enormous input of energy is necessary to break them from the nucleus. In quantum mechanics, however, there is a reasonable probability that the particle will pass through the energetic potential described by the nucleus and manage to escape its influence. Gamow solved a potential model for atomic nuclei and derived a relationship between particle half-life and emission energy.

The alpha decomposition was also solved at the same time by Ronald Gurney and Edward Condon. From then on, it was considered that the particles could enter an energetic tunnel that even crossed the atomic nucleus itself, giving the energetic model complete validity for any application of the "tunnel effect".

After Max Born attended the Gamow seminar, the former recognized the generalities or basics of the mechanics of the effect. He realized that the & # 34; tunnel effect & # 34; It was not restricted solely to nuclear physics, but provided a general result that applies to a very heterogeneous set of systems governed by the laws of quantum mechanics. Nowadays, the theory of energetic tunnels or "tunnel effect" it is being applied to the physics of the cosmology of the universe. Its uses are also being transferred to other areas of technological progress, such as the cold transmission of electrons, and perhaps, more importantly and recognized, to the physics of semiconductors and superconductors. Phenomena such as field emission, vital for flash memories, are elucidated quantum through the consequences of the tunneling effect. This effect is also a resource for amplifying the leak in Very High Scale Integration or VLSI electronics and results in the substantial power drain and heating effect that undermines high speed mobile technology.

Other applications are the scanning tunneling microscope (electron-tunneling) which can present and resolve objects that are too small to be viewed through conventional microscopes. These devices exceed the limitations of light microscopes; visual aberration, wavelength limits by scanning the surface of the object with "tunneling" electrons.

It is notable to verify that it has been shown to be an effect that is carried out naturally by enzymes to catalyze chemical reactions, and it has been shown that these same ones are used to their use when transferring their respective electrons and atoms nuclear, such as hydrogen and deuterium. It has also been observed in the enzyme (GOx) (EC 1.1.3.4) that oxygen nuclei can go through energetic tunnels under physiological conditions.

Simplified explanation

Fig.2

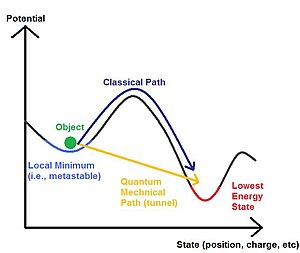
The diagram (Fig.2) compares the tunneling effect with the classical movement of an object. By analogy with gravity, the object tends to move in the direction of the center of the earth. Classically, to reach the minimum state, it must be provided with additional energy. Under the law of quantum mechanics, however, the object can occasionally "go through" the energy state represented by the two slopes and the crest until a minimum state of energy potential is achieved. Considering a mobile that circulates along the trajectory that describes a trough (For the purposes of elucidation, discriminate forces additional to gravity). It is said that it is 500 meters above sea level, the top of the mountain, symbolized by an energetic ridge, reaches 1000 meters, and the plane beyond it is at sea level.. Every instance or material entity that we know tends to its minimum energy level (that is, greater entropy, so the object will try to descend as much as possible). In classical mechanics, as long as a position on the plane is energetically less than that occupied by the mobile, without further compromise with the forces added to the system, it will not have the capacity on its own to reach that position. However, if there were a connecting tunnel between both flanks of the mountain, the mobile would move through it without the need for additional energy at the same gravity. In application to a particle that abides by the precepts of classical mechanics, this is considered "quantum tunneling". Note that this is a valid effect on extremely minimal phenomenological scales, generally, it can only be observed when there is an energetic exchange between particles of atomic size or smaller, in which the potential of the exchange or transfer with the forces that this involves, it transforms it into a notably more complex phenomenon, and in which there are no communicating vessels between tunnels of increasing length. This phenomenon, as it has been exposed before, only allows to graduate the energy of the space that the particle travels in a decreasing way and in accordance with the second law of thermodynamics.

Calculus in semiclassical systems

Consider the timeless form of Schrödinger's equation for a one-dimensional particle, under the influence of a potential "coline." ${displaystyle V(x)}$ .

${displaystyle -{frac {hbar ^{2}}{2m}}{frac {d^{2}}{dx^{2}}}Psi (x)+V(x)Psi (x)=EPsi (x)}$

Now, let's recover the wave function ${displaystyle Psi (x)}$ as an exponential of a function.

${displaystyle Psi (x)=e^{Phi (x)}, mathrm {con} quad Phi ''(x)+Phi '(x)^{2}={frac {2m}{hbar ^{2}}}left(V(x)-Eright).}$

Separate ${displaystyle Phi '(x)}$ in real and imaginary parts, using for this the functions of real variable A and B.

${displaystyle {begin{cases}Phi '(x)=A(x)+iB(x)\A'(x)+A(x)^{2}-B(x)^{2}={frac {2m}{hbar ^{2}}}left(V(x)-Eright)end{cases}}}$ ,

because the pure imaginary part disappears due to the real evaluation of the right hand side:

${displaystyle ileft(B'(x)-2A(x)B(x)right)=0}$

The following is to take the semi-classical approach to resolve the equation. This means we'll have to expand every function as a superserie in $hbar$ . From the equations, we infer that the superseries should begin, at least an order of ${displaystyle hbar ^{-1}}$ to satisfy the real part of them. But when the calculation requires a reasonably more accurate classic limit, we will also need to start with an order of magnitude superior to Planck's constant as possible.

${displaystyle A(x)={frac {1}{hbar }}sum _{k=0}^{infty }hbar ^{k}A_{k}(x),qquad B(x)={frac {1}{hbar }}sum _{k=0}^{infty }hbar ^{k}B_{k}(x).}$

The limitations on the terms of least order are:

${displaystyle A_{0}(x)^{2}-B_{0}(x)^{2}=2mleft(V(x)-Eright), mathrm {con} A_{0}(x)B_{0}(x)=0}$

If the amplitude varies slowly compared to the phase, we specify ${displaystyle A_{0}(x)=0}$ and we get:

${displaystyle B_{0}(x)=pm {sqrt {2mleft(E-V(x)right)}}}$

which is only valid when more energy is available than potential - classical movement. Then the same procedure is applied in the following order of the expansion and we obtain:

${displaystyle Psi (x)approx C{frac {e^{iint dx{sqrt {{frac {2m}{hbar ^{2}}}left(E-V(x)right)}}+theta }}{sqrt[{4}]{{frac {2m}{hbar ^{2}}}left(E-V(x)right)}}}}$

On the other hand, if the phase varies slowly compared to the amplitude, we can adjust ${displaystyle B_{0}(x)=0}$ and get:

${displaystyle A_{0}(x)=pm {sqrt {2mleft(V(x)-Eright)}}}$

which is valid only if it has greater power than energy - tunneling movement. Solving the following expansion with a higher order, we get:

${displaystyle Psi (x)approx {frac {C_{+}e^{+int dx{sqrt {{frac {2m}{hbar ^{2}}}left(V(x)-Eright)}}}+C_{-}e^{-int dx{sqrt {{frac {2m}{hbar ^{2}}}left(V(x)-Eright)}}}}{sqrt[{4}]{{frac {2m}{hbar ^{2}}}left(V(x)-Eright)}}}}$

It is apparent by the denominator that both approximate solutions are removed from the classic curvature point ${displaystyle E=V(x)}$ . What we have are the approximate solutions beyond the potential of "colina" and below it. Beyond this, the particle behaves like a free wave - the phase is oscillating. Below, the particle suffers exponential changes in the amplitude.

In a specific tunneling problem, we should suspect that the amplitude of the transition is proportional to

${displaystyle e^{-int dx{sqrt {{frac {2m}{hbar ^{2}}}left(V(x)-Eright)}}}}$

, so, in this way, the effect is exponentially complicated by long deviations from the classic motor permissivity. But to complete it, we must find the approximate solutions somewhere and link the coefficients to achieve a global approach to the problem. We use for this the solutions that are approached on the basis of those found before the classic curvature points ${displaystyle E=V(x)}$ .

Yeah. $x_{1}$ designates a curvature point, and because they are near ${displaystyle E=V(x_{1})}$ , you can expand ${displaystyle 2m/hbar ^{2}left(V(x)-Eright)}$ in a Taylor series:

${displaystyle {frac {2m}{hbar ^{2}}}left(V(x)-Eright)=v_{1}(x-x_{1})+v_{2}(x-x_{1})^{2}+cdots }$

Let's approach only the linear order ${displaystyle {frac {2m}{hbar ^{2}}}left(V(x)-Eright)=v_{1}(x-x_{1})}$

${displaystyle {frac {d^{2}}{dx^{2}}}Psi (x)=v_{1}(x-x_{1})Psi (x)}$

This differential equation looks suspiciously and deceptively simple. Their solutions are Airy functions:

${displaystyle Psi (x)=C_{A}Aileft({sqrt[{3}]{v_{1}}}(x-x_{1})right)+C_{B}Bileft({sqrt[{3}]{v_{1}}}(x-x_{1})right)}$

Supposedly, this solution should connect the solutions found for space points beyond the ridges and under the system. Given two coefficients on one side of the curvature point, we should be able to determine two other coefficients, on the other hand using this local solution that connects them. For this reason, we have now found a relationship between ${displaystyle C,theta }$ and ${displaystyle C_{+},C_{-}}$ .

Fortunately, Airy functions are asymptotic to sines, cosines, and exponential functions, within the very limits that define them. The relation, then, is determined as follows:

${displaystyle C_{+}={frac {1}{2}}Ccos {left(theta -{frac {pi }{4}}right)}}$
${displaystyle C_{-}=-Csin {left(theta -{frac {pi }{4}}right)}}$

Now, we can build global solutions and solve "tunneling" problems. The transmission coefficient,

${displaystyle left|{frac {C_{mbox{transmitida}}}{C_{mbox{reflejada}}}}right|^{2}}$

for a "tunnel-boring" through an energetic potential or barrier, we obtain that it must be:

${displaystyle T^{2}={frac {e^{-2int _{x_{1}}^{x_{2}}dx{sqrt {{frac {2m}{hbar ^{2}}}left(V(x)-Eright)}}}}{left(1+{frac {1}{4}}e^{-2int _{x_{1}}^{x_{2}}dx{sqrt {{frac {2m}{hbar ^{2}}}left(V(x)-Eright)}}}right)^{2}}}}$

Where, ${displaystyle x_{1},x_{2}}$ are but the two classic curve points defined by the potential barrier. If we take the classic limit of all other parameters greater than Planck constant, abbrevied as ${displaystyle hbar rightarrow 0}$ , we can see that the transmission coefficient tends to zero. This classic limit can virtually fail, but it is easier to solve, as is the case of quadratic potential.

In popular culture

In the "Drama-Future" ("Future-Drama") episode The Simpsons, Homer and Bart cross a mountain where you can read "Quantum tunnel" (quantum tunnel)
In the science fiction series SlidersThe main characters travel to parallel universes using the "tunel effect through an Einstein-Rosen-Podolsky door."

In the science fiction series Zeta Disconnect, the gate that the main characters use to travel through time is referred to as a quantum tunnel.
In the video game Supreme Commanderhumans use the tunnel effect as a means of teleportation, which means they can colonize very distant areas.

In the novel Rescue in time by Michael Crichton, the characters make use of the tunnel effect as an experiential medium for time travel.

Kitty Pryde, a character of the Marvel comics, uses it to cross the walls.

Contenido relacionado

Más resultados...