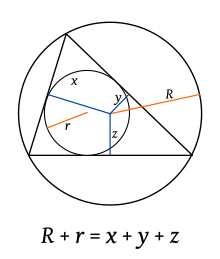Triangle
In plane geometry, a polygon with three sides is called a triangle, trigon or trigonoid. The points common to each pair of sides are called the vertices of the triangle.
A triangle has three interior angles, three congruent parts of exterior angles, three sides, and three vertices, among other elements.
Triangles that are not in a plane
If it is contained in a flat surface it is called a triangle or trigon, a less common name for this type of polygon. If it is contained in a spherical surface it is called a spherical triangle. Represented, in cartography, on the earth's surface, it is called a geodetic triangle.
Elements
Vertices
Each of the points that determine a triangle. Like the vertices of a polygon, they are usually denotated by Latin capital letters: A,B,C,...... {displaystyle A,B,C,dots }. Yeah. AB+BC=AC{displaystyle AB+BC=AC}, there is no triangle to determine A,B{displaystyle A,B} and C{displaystyle C}.
A triangle is named, then, like any other polygon, successively designating its vertices, for example ABC. In the case of the triangle, the vertices can occur in any order, by any of the 6 possible ways (ABC, ACB, BAC, BCA, CAB, CBA), corresponds to a tour of its perimeter. This is no longer true for polygons with more vertices.
Sides
Each pair of vertices determines a segment, known as a side of the triangle. No matter the order of the vertices to name a side so AB, BA name the same side.
The sides of the triangle are denoted, like all segments, by their endpoints: AB, BC and AC.
To name the length on one side, the name of the opposite vertex is usually used, converted to a Latin miniscula: a{displaystyle a} for BC, b{displaystyle b} for AC, c{displaystyle c} for AB.
The sum of the sides of a triangle is known as perimeter, denoted by p or 2sfulfills the equation p=2s=AB+BC+CA{displaystyle p=2s=AB+BC+CA}
Angles
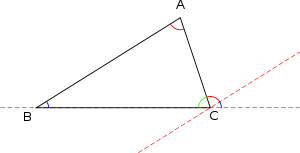
Each pair of sides with a common origin at the vertex of a triangle and containing two of those concurrent sides is called a angle of the triangle or -occasionally- an interior angle.
The general notation for the angle between two segments OP and OQ long and at the end O That's it. POQ^ ^ .{displaystyle {widehat {POQ}}.
It is also possible to use a lowercase letter -usually a Greek letter- surmounted by a circumflex (strictly speaking, angles must be designated by uppercase letters and their measure by lowercase, but often the same names are used for both in order to simplify the notation). In the case of a triangle, the angle between two sides can still, for tolerance and in the absence of ambiguity, be designated by the name of the common vertex, surmounted by a circumflex accent. In summary, in the example you can see the angles:
- α α ^ ^ =a^ ^ =A^ ^ =BAC^ ^ ,β β ^ ^ =b^ ^ =B^ ^ =ABC^ ^ ,γ γ ^ ^ =c^ ^ =C^ ^ =ACB^ ^ .{widehat {widehat {alpha}}={widehat {a}}={widehat {a}}={widehat {BAC}}, {widehat {beta}}}{widehat {b}}{widehat {b}{b}}{widehat {b}}{widehat}}{cHFFFF}}}{cHFFFFFFFFFFFFFF}}}}}{cHFFFF}}{cHFFFFFF}}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}}}}}}}}}{cHFFFFFFFFFFFF}}}{cHFFFFFFFFFFFF}}}}}}}{cHFF}{cHFFFF}{cHFFFFFFFFFFFFFF}{cHFFFFFF}}}}{cHFF}}{cHFFFFFFFF}}{cHFF}}}}}{
An angle whose vertex coincides with one of the vertices of the triangle and its sides: are the extension of a triangular side and the other angular side contains a triangular side, is called external angle. At each triangular vertex there are two exterior angles.
| Vetices | A{displaystyle {text{A}}} | B{displaystyle {text{B}}} | C{displaystyle {text{C}}} |
| Side (as a segment) | BC{displaystyle {text{BC}}} | AC{displaystyle {text{AC}}} | AB{displaystyle {text{AB}}} |
| Side (as length) | a{displaystyle a} | b{displaystyle b} | c{displaystyle c} |
| Angles | α α ^ ^ =a^ ^ =A^ ^ =BAC^ ^ {displaystyle {widehat {alpha}}={widehat {a}}={widehat {a}}}={widehat {BAC}}}}} | β β ^ ^ =b^ ^ =B^ ^ =ABC^ ^ {displaystyle {widehat {beta}}={widehat {b}}={widehat {b}}}{widehat {b}}}{widehat {bb}}}}}}} | γ γ ^ ^ =c^ ^ =C^ ^ =ACB^ ^ {displaystyle {widehat {gamma}}={widehat {c}}={widehat {c}}={widehat {ACB}}}} |
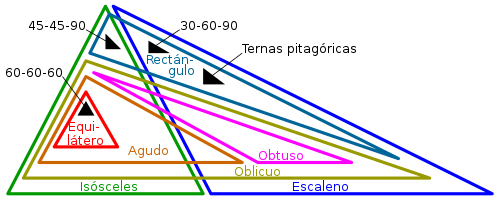
Classification of triangles
Triangles can be classified by the ratio of the lengths of their sides or by the width of their angles.
By the measure of its sides
By the measure of its sides, every triangle is classified as:
- equilateral triangle(Latin) aequilatěrus, composed of aequus, 'equal' and latus, 'late', in Greek: σόπλευρον, romanized: isopleuron, literally 'like sides') when the three sides of the triangle have the same length (the three inner angles measure 60 degrees or π π /3{displaystyle pi /3,} radian).
- Triangle isosceles (from the Greek.σος "equal" and σκιλη "piernas", that is, "with two equal legs"), are those that have at least two congruent sides, that is, the same. The angles that oppose these sides have the same measure. (Tales de Mileto, Greek philosopher, showed that an isosceles triangle has two equal angles, thus establishing a relationship between lengths and angles; equal sides, equal angles).
- A triangle is isosceles when it has two equal sides; this does not rule out that the three sides are equal, so that every equilateral triangle is isosceles, but the reciprocal phrase is not fulfilled.
- Be the triangle ABC isosceles, where b = c then the opposite angles are equal, i.e B = C. It is also fulfilled that B' = C' being these external angles. In addition, equality is met
- A + 2B = A +2C = 180o;
- A' + 2B' = A' + 2C' = 360o; A' = 2C = 2B; B'= C'=A+B = A+C
- ma=ha=vA=124b2− − a2{displaystyle m_{a}=h_{a}=v_{a}={frac {1}{2}}}}{sqrt {4b^{2}-a^{2}}}}}}}}}}}{displaystyle m_{a} where ma,ha,vA{displaystyle m_{a},h_{a},v_{a}}}} It's the middle, the side height a and his angle bisectr A opposite.
- Bathing triangle (from the Greek σκαληνός "desigual"), if all its sides have different lengths (in an escalen triangle there are no two angles that have the same measure).
 |  |  |
|---|---|---|
| Equilateral | You know what? | Bathing ladder |
By the width of its angles
|
By the amplitude of their angles, triangles are classified as:
- Triangle rectangle: if you have a straight inner angle (90°). On both sides that make up the right angle are called Catetos and the other side hypotenuse.
- Dark triangle: when none of its inner angles is straight (90°). Therefore, the obtussangle and acutanguous triangles are oblique. Any triangle is either rectangle or oblique.
- Dark triangle: if one of its inner angles is obtuso (over 90°); the other two are acute (under 90°).
- Triangle acutángulo: when its three interior angles are less than 90°.
 |  |  |
|---|---|---|
| Rectangle | Obtussant | Accutangle |
| {displaystyle underbrace {qquad qquad qquad qquad qquad qquad } _{}} | ||
| Oblique | ||
Classification according to the sides and angles of the triangle
Acute triangles can be:
- Triangle acutanus isosceles: with all the sharp angles, being two equals, and the other different. This triangle is symmetrical about its height on the different side.
- Acutaneous triangle: with all its sharp angles and all different, it has no axis of symmetry.
- Triangle equatedrongue: its three sides and its three angles are equal. The three heights are axis of symmetry (divide the triangle in two equal triangles).
Right triangles can be:
- Triangle rectangle isosceles: with a straight angle and two equal sharps (45° each), two sides are equal and the other different: the equal sides are the ghettos and the different is the hypotenuse. It is symmetrical regarding the height of the hypotenuse, which passes through the right angle.
- Bathing ladder rectangle triangle: it has a straight angle, and all its sides and angles are different.
Obtuse triangles can be:
- Triangle isosceles: it has an obtuse angle, and two equal sides that are those that form the obtuse angle; the other side is greater than these two.
- Bathing ladder obtangle triangle: it has an obtuso angle and all its sides are different.
| Triangle | equilateral | isosceles | Bathing ladder |
|---|---|---|---|
| acutangule |  |  |  |
| Rectangle |  |  | |
| obstruction |  |  |
Qualitative classification of a triangle
The measure of the quality of a triangle (abbreviated as CT) is determined by the product of three factors that are obtained from the sum of two of its sides minus the third in a cyclical way, divided by the product of its three sides; and is represented by the following formula:
- CT=(a+b− − c)(b+c− − a)(c+a− − b)abc{displaystyle CT={frac {(a+b-c)(b+c-a)(c+a-b)}{abc}}}}
where a, b, c are the lengths of the sides of the triangle.
So, if
- CT = 1 is an equilateral triangle.
- CT = 0 is a degenerate triangle.
- CT 0.5 is a good quality triangle.
In other words, the quality of the triangle approaches zero when the Euclidean distance of one of its sides is close to zero or when the three points of the triangle tend to be collinear.
The quality of triangles has many applications in triangulation methods such as Delaunay triangulation because a series of points in space need to be generated so that the mesh generated is of good quality due to the number of points that are well distributed in a two-dimensional space because when a value or magnitude is assigned to each point of the mesh, the triangle approximation will have a greater error and the solution would be to continue assigning points in the space of two dimensions so that the approximation is better and the error decreases.
Triangle Congruence
Two triangles are congruent if there is a correspondence between their vertices in such a way that the angle of the vertex and the sides that compose it, in one of the triangles, are congruent with those of the other triangle.
Postulates of Congruence
Congruence Theorems
| Triangle | Theorems of congruence |
|---|---|
| Theorem AAL (Language, Angle, Side)
Two triangles are congruent if two angles and one side, not understood between the angles, have the same measure and length, respectively. |
Congruence of Right Triangles
- Criterion HC (Hipotenusa, Cateto). Two rectangles triangles are congruent if the hypotenuse and the cathet of one of the triangles have the same measure as the corresponding ones of the other.
- Criteria CC (Cateto, Cateto). Two rectangle triangles are congruent if one of the triangles have the same measure as the corresponding caetos of the other.
- Criteria HA (Hipotenusa, Angle). Two rectangles are congruent if the hypotenuse and a sharp angle of one of the triangles have the same measure as the corresponding ones of the other.
- Criteria CA (Cateto, Angle). Two rectangles are congruent if the cathet and a sharp angle (the adjacent or the opposite) of one of the triangles have the same measure as the corresponding ones of the other.
Similar triangles
- Criteria AA (Angle, Angle). If two of their angles are similar.
- LAL Criterion (Lado, Angle, Side). If two of their sides are proportional and the angle between them is congruent.
- LLL Criterion (Lado, Lado, Lado). If their three sides are proportional.
Similarity of Right Triangles
Two right triangles are similar if they meet at least one of the following criteria:
- If one has a sharp angle of equal magnitude than a sharp angle of the other.
- If one has the two proportional to each other.
- If one has a caeto and the proportional hypotenuse with the other.
Triangle crown
Two similar triangles with parallel sides and a common circumcenter (center of the circumscribed circle) are considered. The intersection of the exterior of the triangle with the smallest area with the interior of the triangle with the largest area joined with the two triangles forms a region in the plane called the triangular crown.
The border of this region is the union of the two triangles. A point is interior if it is between the intersections determined by a ray originating from the circumcenter with the homologous sides. The set of interior points is the interior of the region. A point is on the outside of the region if it is neither on the boundary nor on the interior. The interior is convex, open and connected. The border is the disjoint union of two closed traverses. The exterior is a disconnected, open and non-convex set. The triangular corona is a closed, connected and convex set. The triangular corona is homeomorphic with the circular corona, they have the same topological properties.
Properties of triangles
A triangle can be defined as a polygon with three sides, or as a polygon with three vertices. The triangle is the simplest polygon and the only one that does not have a diagonal. Three non-aligned points always define a triangle (both in the plane and in space).
If we add a fourth point coplanar and not aligned, we obtain a quadrilateral that can be divided into triangles like the one in the figure on the left. On the other hand, if the fourth added point is not coplanar and not aligned, a tetrahedron is obtained, which is the simplest polyhedron and is made up of 4 triangular faces.
Every polygon can be divided into a finite number of triangles, this is achieved by triangulation. The minimum number of triangles needed for this division is n-2, where n is the number of sides of the polygon. The study of triangles is essential for the study of other polygons, for example for the demonstration of Pick's Theorem.
In Euclidean geometry the sum of the three internal angles of a triangle is always 180°, which is equal to π radians:
α α +β β +γ γ =180 =π π {displaystyle alpha +beta +gamma =180{}^{circ}=pi } |
Euclid had demonstrated this result in his Elements (proposition I-32) in the following way: draw a line parallel to the line (AB) that passes through C. Being parallel, this line and the line (AB) forms equal angles with the line (AC), coded in red in the figure on the right (alternate-internal angles). Similarly, angles coded in blue are equal (corresponding angles). On the other hand, the sum of the three vertex angles C is the straight angle. So the sum of the measures of the red, green, and blue angles is an angle of 180° (or π radians). In conclusion, the sum of the angles of a triangle is 180°.
This property is the result of Euclidean geometry. It does not hold in general in non-Euclidean geometry.
Other properties
- The sum of the lengths of two sides of a triangle is always greater than the length of the third side.
- The value of the average base of a triangle (segment that unites two midpoints of two sides) is equal to half the side parallel.
- The triangles (three-sided polygons) are the only polygons always convex, cannot be concaves, since none of their three angles can exceed 180 degrees or π π {displaystyle pi } radian.
- For any triangle the Theorem of the bosom is verified: "The sides of a triangle are proportional to the boobs of opposite angles":
- awithout (α α )=bwithout (β β )=cwithout (γ γ ){displaystyle {frac {a}{sin(alpha ,)}}}={frac {b}{sin(beta ,)}}={frac {c}{sin(gamma ,)}}}}}}}}
- Any convex polygon of n sides can be broken into n-2 triangles with disjoint interiors, considering a vertice of which n-3 segments are traced to non-contiguous vertices.
- For any triangle the Theorem of the Cosine is verified: "The square of one side is equal to the sum of the squares of the other side less than the double of the product of these sides by the cosine of the angle understood":
- a2=b2+c2− − 2bc⋅ ⋅ # (α α ){displaystyle a^{2}=b^{2}+c^{2}-2bccdot cos(alpha ,),}
- b2=a2+c2− − 2ac⋅ ⋅ # (β β ){displaystyle b^{2}=a^{2}+c^{2}-2accdot cos(beta ,),}
- c2=a2+b2− − 2ab⋅ ⋅ # (γ γ ){displaystyle c^{2}=a^{2}+b^{2}-2abcdot cos(gamma ,),}
- For any rectangle triangle, whose cathets measure a and band whose hypotenuses measure cthe Theorem of Pythagoras is verified:
- c2=b2+a2{displaystyle c^{2}=b^{2}+a^{2},}
From the previous equation, 3 practical application formulas can be easily deduced:
| a=c2− − b2{displaystyle a={sqrt {c^{2}-b^{2}}}}} | b=c2− − a2{displaystyle b={sqrt {c^{2}-a^{2}}}}}} | c=a2+b2{displaystyle c={sqrt {a^{2}+b^{2}}}}} |
- Through rotation, translation, axial symmetry and punctual symmetry the image of a triangle is a triangle congruent to the proposed one.
- Given a triangle in the Cartesian plane you can find the equation of a circumscribed parable of horizontal or vertical axis
Notable Points
Geometrically, several cases can be defined that are linked to a triangle:
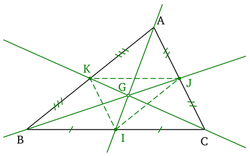
- Baricentro: is the point that is at the intersection of the medians, and it is equivalent to the ideal center of gravity of a triangle.
- Circuncent: it is the center of the circumscribed circle, the one that passes through the three vertices of the triangle. It is at the intersection of the mediatric sides.
- Incenter: it is the center of the inscribed circle, that which is tangent to the sides of the triangle. It is located at the intersection of the angles bisectrices.
- Ortocentro: is the point that is at the intersection of heights.
- Exincentives are the centers of the extruded circles. It is located at the intersection of an internal bisectr and two external angles.
The only case in which the centroid, incenter, orthocenter, and circumcenter coincide is in an equilateral triangle.
Calculating the sides and angles of a triangle
In general, there are several accepted methods for calculating the length of a side and the measure of an angle. While certain methods may be suitable for calculating the values of a right triangle, others may be required in more complex situations.
To solve triangles (in general) the theorems of sine and cosine are usually used, for the special case of right triangles the Pythagorean Theorem is generally used.
Trigonometric ratios in right triangles
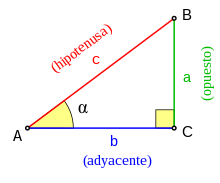
In right triangles, the trigonometric ratios of sine, cosine, and tangent can be used to find unknown angles and side lengths. The sides of the triangle are named as follows, with respect to one of the acute angles:
- The hypotenuse is the opposite side to the right angle. It is the longest side of a rectangle triangle.
- The opposite cathet is the opposite side to the sharp angle considered.
- The adjacent cathet is the cathet that forms the sharp angle considered.
Sine, Cosine, and Tangent
The sine of an angle is the quotient between the length of the opposite leg and the length of the hypotenuse.
- senα α =oppositehypotenuse=ac.{displaystyle {text{sen}}alpha ={frac {color {ForestGreen}{textrm {opposed}}}}{color {Red}{textrm {hipotenusa}}}}}}{frac {a}{c}}}{. !
The cosine of an angle is the quotient between the length of the leg of the adjacent side and the length of the hypotenuse.
- # α α =adjacenthypotenuse=bc.{displaystyle cos alpha ={frac {color {Blue}{textrm {adyacente}}}}{color {Red}{textrm {hipotenusa}}}}}}}}{{frac {b}{c}{c}}}}}}}{. !
The tangent of an angle is the quotient between the length of the opposite leg and the length of the adjacent leg.
- So... α α =oppositeadjacent=ab.{displaystyle tan alpha ={frac {color {ForestGreen}{textrm {oppos}}}{color {Blue}{textrm {adyacente}}}}}}}}{{frac {a}{b}}}}}}}. !
Note: The quotients of the three relationships above do not depend on the size of the right triangle.
Inverse functions
The inverse trigonometric functions can be used to calculate the interior angles of a right triangle having the length of any two sides.
Arcsin (arcosine) can be used to calculate an angle with the length of the opposite leg and the length of the hypotenuse.
- θ θ =arcsin (oppositehypotenuse){displaystyle theta =arcsin left({frac {color {ForestGreen}{textrm {oppos}}}{color {Red}{textrm {hipotenusa}}}}}}}{right}
Arccos (arc cosine) can be used to calculate an angle with the length of the adjacent leg and the length of the hypotenuse.
- θ θ =arccos (adjacenthypotenuse){displaystyle theta =arccos left({frac {color {Blue}{textrm {adyacente}}}{color {Red}{textrm {hipotenusa}}}}}}}{right}
Arctan (arctangent) can be used to calculate an angle with the length of the opposite leg and the length of the adjacent leg.
- θ θ =arctan (oppositeadjacent){displaystyle theta =arctan left({frac {color {ForestGreen}{textrm {opposed}}}{color {Blue}{textrm {adyacente}}}}}}}{right)}
In introductory geometry and trigonometry courses, the notation sin−1, cos−1, etc., is often used instead of arcsin, arccos, etc.. However, the notation of arcsin, arccos, etc., is standard in higher mathematics where trigonometric functions are commonly raised to powers, as this avoids confusion between the multiplicative inverse and the inverse function.
Notable elements of a triangle
Inside
Given a point in the Euclidean plane, we will say that this is interior of a triangle if, when drawing a line through it, said point is between the cuts with the sides of the triangle. Otherwise, a point is an interior point of a triangle, if it is inside each angle of the triangle. If we consider a triangular region, its interior coincides with the defined interior according to the usual topology of the plane.
Border and exterior
The three sides of a triangle make up its borderline and the points in the plane that are neither inside nor on the border are on the outside of the triangle. The union of the interior, of the triangle (border) and of the exterior is equal to the plane of the triangle. Each pair of the aforementioned sets has an empty intersection or they are mutually disjoint sets.
Topological Equivalence
Any triangle is equivalent to a simple closed curve; especially to a circle. That is, between a circle and a triangle a bijective and bicontinuous application can be established.
Cevian
Ceviana is a line that passes through a vertex of a triangle and through the line that contains the opposite side; some authors include the sides of the triangle as cevians. They are considered interior cevians, if they contain points of the triangular interior; and exterior cevians, when it passes through the exterior of the triangle.
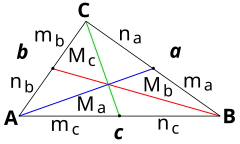
Median
The line segment from a vertex to the midpoint of the opposite side of a triangle is called the median. In some countries (for example: Chile) are called gravity transversals, reserving in those places the term median for what is usually called median parallel.
Some properties of medians are:
- The three medians of a triangle converge at a point -point G- Called. downtown or ♪ of the triangle.
- Each of the three medians divides the triangle into two triangles of equal areas. The distance between the baricentro and a vertex is 2/3 of the length of the median.
- The three medians divide the triangle into 6 triangles of equal areas.
From Apolonio's theorem, also called "theorem of the median", several practical formulas can be deduced (valid for any triangle), these allow calculating from the knowledge of three elements, a fourth element unknown (the elements in question are sides and medians). The following table shows a summary of them (with notation according to the figure in the table itself):
- By joining the feet of the medians (middle point of each side) you get a triangle similar to the original and its area is 1/4 of the area of this.
- ma2 + mb2 + mc2 = 3/4(a)2 + b2 +c2), link between the three mediums and the respective sides of a triangle.
Perpendicular bisector and circumcircle
It is called mediatrix on one side of a triangle to the perpendicular straight to that side drawn by its midpoint (also called simetral). The triangle has three mediatrines, one on each side [chuckles]AB]{displaystyle [AB]}, [chuckles]AC]{displaystyle [AC]} and [chuckles]BC]{displaystyle [BC]}.
The three mediatrics of a triangle are concurrent at a point O{displaystyle O} the three vertices. The centre circumference O{displaystyle O} and radio OA{displaystyle OA} which passes through each of the three vertices of the triangle is the circumscribed the triangle, and its center is called circumcentro.
- In an acutaneous triangle, the center of the circumscribed circumference is within the triangle.
- In an obtussangle triangle, the center of the circumscribed circumference is outside the triangle.
- In a rectangle triangle, the center of the circumscribed circumference is the midpoint of the hypotenuse.
- Property
A triangle is right-angled if and only if the center of its circumcircle is the midpoint of its hypotenuse.
Bisector, incircle, and excircle
The bisectors of a triangle are the bisectors of its angles. There are internal (usual) and external bisectors to these angles.
The three internal bisectors of a triangle are concurrent at a point O. The incircle of the triangle is the only circle tangent to the three sides of the triangle and is inside the triangle. Its central point is the incenter, which is the center of the inscribed circle in the triangle.
Furthermore, the exterior bisectors of two angles concur with the interior bisector of the remaining angle at points called exincenters, which are the centers of the exincircles of the triangle. There are 3 exincenters, as well as 3 exincircles. The excircles are tangent to one side and to the extension of the other two.
The distance from a vertex of the triangle to the points of intersection of the circle inscribed in the triangle with the sides that intersect at said vertex by power of a point is the same, therefore the lengths of the sides of a triangle are a=x+y, b=y+z, c=z+x, this way of denoting the sides of a triangle is known as Ravi transformation, in a right triangle the sides are x+r, r+y, y+x with r the radius of the incircle of the triangle.
Length of a bisector
vA=2b+cbcp(p− − a){displaystyle vA={frac {2}{b+c}}{sqrt {bcp(p-a)}}}}where vA is the angle bisector A; a, b, c, sides of the triangle and p the semiperimeter; being
p=a+b+c2{displaystyle p={frac {a+b+c}{2}}}}}
Steiner's Theorem
Being ra,rb,rc{displaystyle r_{a},r_{b},r_{c}}} radius of the circumferences exinscribed from a triangle ABC; R and r radios of the circumscribed circle and inscribed in the same triangle, respectively, then the equation follows:
4R+r=ra+rb+rc{displaystyle 4R+r=r_{a}+r_{b}+r_{c}
Comparison with height
For any triangle, where es = the smallest height, el = the smallest bisector and S the area, the following is true
- h23≤ ≤ l23≤ ≤ S{displaystyle {frac {h^{2}{sqrt {3}}}}{leq {frac {l^{2}{sqrt {3}}}}{leq S}}
Symedian
The line (cevian) that is symmetric to the median is called symedian, the axis of symmetry being the bisector with the same vertex.
Propositions
- the simedian divides the corresponding side of the triangle directly proportional to the squares of the other two sides.
- the simedian is the set of the points for which the distances to the sides that understand it are proportional to the lengths of these.
- Lemoine Point
The Lemoine point is an interior point of a triangle for which the sum of the squares of their distances to the sides is the minimum. It is also named point of Lemoine- L' Huiller
- The Lemoine point matches the intersection of the simedians.
Altitudes and orthocenter
His name is height of a triangle to the perpendicular straight segment that unites a vertex of the triangle with the opposite side of this or its prolongation. The opposite side is called base of the triangle. All triangles have three heights. These 3 heights are cut at a single point H{displaystyle H} (son) concurrent), called ortocentro of the triangle.
- Properties
- A triangle is rectangle if and only if its orthocenter is the right vertex of the triangle.
- A triangle is obtussive if and only if its orthocentre is outside the triangle.
- A triangle is acutaneous if and only if its orthocentre is within the triangle.
Heights times the length of their sides
For any triangle ΔABC, given the length of its sides (a, b, c), the respective lengths of the heights (h a, hb, hc) applying the following formulas:
- ha=Δ Δ a{displaystyle h_{a}={frac {tau }{a}}}}
- hb=Δ Δ b{displaystyle h_{b}={frac {tau }{b}}}}
- hc=Δ Δ c{displaystyle h_{c}={frac {tau }{c}}}}
Where ha is the corresponding height on the side a, hb is the corresponding height on the side b, hc is the corresponding height on the side c and the term Δ Δ {displaystyle tau } is:
Δ Δ =12(a+b− − c)(a− − b+c)(− − a+b+c)(a+b+c){displaystyle tau ={frac {1}{2}}{sqrt {(a+b-c)(a-b+c)(-a+b+c)(a+b+c)}}}}}}}}The height of side a can be found using the following formula
ha=2ap(p− − a)(p− − b)(p− − c)::↓ ↓ {displaystyle h_{a}={frac {2}{a}}{sqrt {p(p-a)(p-b)}}:where ha is the height indicated; a, b, c sides and sides p the semiperimeter of the triangle. For the other two heights it is enough to change the denominator on the respective side in the formula ↓ ↓ {displaystyle}.
Relation to the inradius
Given a triangle and its three altitudes ha, hb and hc and the radius r of its inscribed circle (inradius), holds the following equality:
- 1ha+1hc+1hc=1r{displaystyle {frac {1}{h_{a}}}} +{frac {1{h_{c}}}}}{frac {1}{h_{c}}}}}}}{frac {1}{1}{r}}}}}
Euler line
The three points H{displaystyle H}, G{displaystyle G} and O{displaystyle O} are lined up in a straight line called Straight from Euler of the triangle and verifies the relationship of Euler:
- OH=3OG{displaystyle OH=3OG,}
The midpoints of the three sides, the three feet of the heights and the midpoints of the segments [chuckles]AH]{displaystyle [AH]}, [chuckles]BH]{displaystyle [BH]} and [chuckles]CH]{displaystyle [CH]} are in the same circumference called Euler circumference or circumference of the nine points of the triangle.
Carnot's Theorem
The Carnot theorem states that, for an acutaneous triangle of ABC vertices, the sum of the respective distances x,and,z{displaystyle x,y,z} from the circumcenter to the sides of the triangle is equal to the sum of the radios R,r{displaystyle R,r} of the circumscribed and inscribed circles, respectively, of the triangle:
R+r=x+and+z{displaystyle R+r=x+y+z}.Area of a triangle
Usual and elementary formula
Using a side that is called, in this context, base and its height, perpendicular (and measure) drawn from the vertex placed on said side or its prolongation. The corresponding height is subscripted with a letter on the side.
The area of a triangle is equal to the semiproduct of the base times its respective height.
A=b× × hb2{displaystyle A={frac {btimes h_{b}}{2}}}}
A=a× × ha2{displaystyle A={frac {atimes h_{a}}{2}}}}
A=c× × hc2{displaystyle A={frac {ctimes h_{c}{2}}}}
This is true for any rectilinear triangle. The area is the measure of a triangular region, that is, the union of the three segments and its interior. It is deduced based on the area of a parallelogram.
Area with Heron's formula
Knowing the length of the three sides a, b and c, we can calculate the area for any Euclidean triangle. First, the semi-perimeter s is calculated and then Heron's formula is applied, (it is not required to know the height).
s=12(a+b+c){displaystyle s={frac {1}{2}}(a+b+c)}
A♪ ♪ rea=s(s− − a)(s− − b)(s− − c){displaystyle mathrm {{acute {A}rea} ={sqrt {s(s-a)(s-b)}}}}
- If the perimeter of a triangle is considered constant, the one with the largest area is the equilateral triangle.
If the Ravi Transformation is applied to the sides of the triangle we have that the sides are x+y, y+z, z+x and the area of the triangle is
A♪ ♪ rea=xandz(x+and+z){displaystyle mathrm {{acute {A}rea} ={sqrt {xyz(x+y+z}}}}}}
Areas with side lengths
Knowing the length of the three sides a, b and c, we can calculate the area for any Euclidean triangle, (these formulas do not require pre-calculating the semi-perimeter or knowing the height).
A♪ ♪ rea=14(a+b− − c)(a− − b+c)(− − a+b+c)(a+b+c){displaystyle mathrm {{acute {A}rea} ={frac {1{4}}}{sqrt {(a+b-c)(a-b+c)(-a+b+c)(a+b+c)}}}}}}
A♪ ♪ rea=142(a2b2+a2c2+b2c2)− − a4− − b4− − c4{displaystyle mathrm {{acute {A}}rea} ={frac {1{4}}}{sqrt {2left(a^{2}b^{2}+a^{2}c^{2}{2}+b^{2}c^{2}c^{2}c^{2}{2}{2}}{2}{2}{2}{2}{2}{2}{2}{2})})}c^{2}{2})}c^{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}}}}{2}{2}{2}{right)}{right)}{right)})}{right)}
Upper bound for area
If A is the area of a triangle and a,b and c its sides, the following inequality is verified
- A≤ ≤ 2(ab+ac+bc)− − a2− − b2− − c243{displaystyle Aleq {frac {2(ab+ac+bc)-a^{2}-b^{2}-c^{2}}{4{sqrt {3}}}}}}}}}}}}}}}
Area with radii of linked circles and sides
S=abc4R{displaystyle S={frac {abc}{4R}}}S=pr{displaystyle S=pr}S=(p− − a)ra=(p− − b)rb=(r− − c)rc{displaystyle S=(p-a)r_{a}=(p-b)r_{b}=(r-c)r_{c}}}S=rrarbrc{displaystyle S={sqrt {r_{a}r_{b}r_{c}}}}}}S=12Rhahbhc{displaystyle S={sqrt {{frac {1}{2}}{Rh_{a}h_{b}h_{c}}}}}}S=2R2abchahbhc{displaystyle S={frac {2R^{2}}{abc}}{h_{ah}_{b}h_{c}}}}{b}}}}}where S is the area; also a,b,c,p{displaystyle a,b,c,p} are the sides and the semiperimeter of the triangle; Rradius of the circumscribed circle or circumcision; r, radio of the inscribed circle or Indian; ra,rb,rc.{displaystyle r_{a},r_{b},r_{c}. ! radios of exinscribed circles ha,hb,hc{displaystyle h_{a},h_{b},h_{c}}} are the respective heights.
Area with the length of two sides and the included angle
If in the formula area = ah/2, where h is the height measured on the base a, it is taken into account that
- without C = h/b or what is the same h = b without C, you get that:
- A♪ ♪ rea=ah2=abwithoutC2{displaystyle mathrm {{acute {A}rea} ={frac {a;h}{2}{frac {a;b,;sin ,C}{2}}}}}}},
and likewise:
- A♪ ♪ rea=bcwithoutA2{displaystyle mathrm {{acute {A}rea} ={frac {b;c,sin,a}{2}}}}}and
- A♪ ♪ rea=acwithoutB2{displaystyle mathrm {{acute {A}rea} ={frac {a;c,;sin,b}{2}}}}},
Area with the length of a side and the adjacent angles
If in the formula area = a b sin C / 2 it is taken into account that according to the law of sines b = a sin B / sin A, it is obtained that:
- A♪ ♪ rea=a22withoutBwithoutCwithoutA{displaystyle mathrm {{acute {A}rea} ={frac {a^{2}}{2}}{2}{frac {sin,B;sin,C}{sin,a}}}}}}}}{,
and taking into account that A = π π {displaystyle pi } -B + Cand to be(π π {displaystyle pi } - S) = sen(S)
- A♪ ♪ rea=a22withoutBwithoutCwithout(B+C){displaystyle mathrm {{acute {A}rea} ={frac {a^{2}}{2}}{2}{frac {sin ,B;sin,C}{sin ,(B+C)}}}}}}},
and likewise:
- A♪ ♪ rea=b22withoutAwithoutCwithout(A+C){displaystyle mathrm {{acute {A}}rea} ={frac {b^{2}}{2}}{2}{frac {sin , asin, c}{sin ,(A+C)}}}}}}and
- A♪ ♪ rea=c22withoutAwithoutBwithout(A+B){displaystyle mathrm {{acute {A}rea} ={frac {c^{2}}{2}}{2}{frac {sin , asin ,b}{sin ,(A+B)}}}}}}},
Using Cartesian coordinates
If any triangle (in the Euclidean plane ℝ²), has one of its vertices (suppose A) located at (0, 0) — the origin of the Cartesian coordinates—, and the coordinates of the other two vertices (suppose B y C) are given by B = (x B, yB) and C = (xC, yC), then the area can be computed as ½ of the absolute value of the determinant (reduced to the two arbitrary vertices B and C).
A♪ ♪ rea=12日本語det[chuckles]xBxCandBandC]日本語=12日本語xBandC− − xCandB日本語.{displaystyle mathrm {{acute {A}rea} ={frac {1{2}}}}}left implieddet {begin{bmatrix}x_{B}{B}{C}{b}{bmatrix}{bmatrix}{bmatrix}{bm}{frac {1}{b}{B}{B}{B}{bm}{B}}{B}{bm}}{bm. !
A♪ ♪ rea=12日本語xBandC− − xCandB日本語.{displaystyle mathrm {{acute {A}rea} ={frac {1{1{2}}}{B}y_{C}-x_{C}y_{B}. !
If a generic triangle (in the Euclidean plane ℝ²), has its three vertices located arbitrarily (none at the origin), then the equation is:
A♪ ♪ rea=12日本語det[chuckles]xAxBxCandAandBandC111]日本語=12日本語xAandB− − xAandC+xBandC− − xBandA+xCandA− − xCandB日本語{cHFFFFFF}{cHFFFF}{cHFFFFFF}{cHFFFF}{cHFFFF}{cHFFFF}{cHFFFFFF}{cHFFFF}{cHFFFF}{cH}{cHFF}{cHFF}{cHFF}{cHFF}{cH00}{cHFFFFFFFF}{cHFF}{cH00}{cH00}{cH00}{cH00}{cH00}{cHFFFFFFFFFFFF}{cH00}{cHFFFFFFFFFF}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00
A♪ ♪ rea=12日本語(xA− − xC)(andB− − andA)− − (xA− − xB)(andC− − andA)日本語.{displaystyle mathrm {{acute {A}rea} ={frac {1{2}}}{big ⋅}(x_{A}-x_{C})(y_{B}-y_{A})-(x_{A}-x_{B})(y_{C}-y_{A}){bigcult}}}}. !
For a generic triangle (in Euclidean space ℝ³), whose coordinates are { A = (xA, y A, zA), B = (xB, yB, zB) and C = (x C, yC, zC)}, then the area is given by the sum Pythagorean of the areas of the respective projections onto the three principal planes (i.e. x = 0, y = 0 and z = 0):
A♪ ♪ rea=12日本語det[chuckles]xAxBxCandAandBandC111]日本語2+日本語det[chuckles]andAandBandCzAzBzC111]日本語2+日本語det[chuckles]zAzBzCxAxBxC111]日本語2.{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cH00FFFF00}{cH00FFFF00}{cHFFFFFFFF00}{cHFFFF00}{cHFFFF00}{cHFFFF00}{cH00}{cH00FFFFFFFFFFFFFFFFFFFFFFFF00}{cH00}{cH00}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFF00}{cHFFFFFFFFFFFFFFFFFFFF00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00FFFF00}{cH00}{cH00FFFF !
Area of a triangle in space
- They give three points A, B, C of eucliding spaceR3. Vectors can be determined AB and AC, then there is the vector product of such vectors. Half of the module of such a vector product is the area of the triangle ABC.
This formula is still valid in the ℝ2 plane (therefore in the complex plane), taking care to consider the third coordinate equal to 0. However, for ℝn, n > 3, one of the vectors is used as a base, then the cosine of the angle formed by the concurrent sides in A is obtained by means of the scalar product of the vectors corresponding to said sides. Then the sine of such an angle, which leads to find the height of the triangle.
Triangular area in a Euclidean space
In these spaces the scalar (inner) product of vectors is defined. Let a and b be two vectors of any n components of a Euclidean space. The inner product is <a, b> = sum of aibi for i = 1,2,...,n
- has the climbing product of two vectors:a, ba日本語bSPECIAL C. C is the angle between vectors
- knowing the cosine we can calculate sen C = (1-things2 (c) 0.5
- Then the ABC triangle area is A = 0.5×a日本語bΔ×sen C
Area of right triangles with integer sides
When we consider obtaining triangles rectangle with entire sides the general solution of the equation x2+and2=z2{displaystyle x^{2}+y^{2}=z^{2}}}:
{x=m(2uv)and=m(u2− − v2)z=m(u2+v2){displaystyle {begin{cases}x=m(2uv)y=m(u^{2}-v^{2})z=m(u^{2}+v^{2})end{cases}}}}}}}
See also Pythagorean triple
In these formulas, u and v are two arbitrary positive integers of different parity such that u > v and are prime to each other. The positive integer m is any one that covers the cases in which the elements of the Pythagorean triple have a common factor. When m = 1, we have the Pythagorean triples with elements prime to each other two by two. As the reader can appreciate, although these formulas were designed to obtain triples with integer sides, being an identity, they are also valid for real sides, except for the case in which both legs are equal (that the hypotenuse is a diagonal of a square).
If we calculate the area based on the expressions found for the legs, since the surface of a right triangle is equal to the semiproduct of the legs, we are left with a cubic form:
A=xand2;A=m2(u3v− − uv3)=m2uv(u2− − v2){displaystyle textstyle A={frac {xy}{2}};;A=m^{2};(u^{3}v-uv^{3})=m^{2};uv;(u^{2}-v^{2}}}}}}}}}
The numbers of the form uv(u2− − v2){displaystyle uv;(u^{2}-v^{2})}When u and v They are. u ▪ v and unstoppable positive integers and cousins among themselves, are congruent numbers of Fibonacci, introduced in their Liber Quadratorum (1225). There's no known reason for u and v They can't be of different parity. Fibonacci showed that the product of a congruent by a square is also congruent.
Since the area of any triangle can be decomposed into the addition or subtraction of the area of two right triangles, we have two expressions for the area of non-right triangles:
Acutangle: m2uv(u2− − v2)+n2st(s2− − t2){displaystyle m^{2};uv;(u^{2}-v^{2})+n^{2};st;(s^{2}-t^{2})}}Objection: m2uv(u2− − v2)− − n2st(s2− − t2){displaystyle m^{2};uv;(u^{2}-v^{2})-n^{2};st;(s^{2}-t^{2})}}}Not to forget that this is only valid for pairs of right triangles that do not have equal legs. It is a more complicated way of calculating the area of a triangle, and it is also poorly understood. But in some cases, your writing can shed light on issues that otherwise go unnoticed.
Proposition
A triangle with sides a, b and c, inscribed in a circle of radius R, with constant perimeter 2p, reaches its maximum area when all three sides are equal.
In space
The triangle is the shape of the faces of three regular polyhedra:
- tetraedro: four equilateral triangles in the faces and corners formed by the confluence of 3 triangles (is the triangular base pyramid),
- octahedron: eight equilateral triangles on the faces and corners formed by the confluence of 4 triangles (the pyramids of Egypt are half-octahedrons),
- icosaedro: twenty equilateral triangles on the faces and corners formed by the confluence of 5 triangles.
In other cases, the lateral faces of a pyramid are two-by-two triangles with a common edge; likewise, the lateral faces of an antiprism are triangles.
History
The monumental architecture of Egypt's Third and Fourth Dynasty is remarkable evidence that the Egyptians of that time had a relatively sophisticated knowledge of geometry, especially in the study of triangles; although no mathematical documents from the Old Kingdom have come down to us.
The calculation of the area of this figure is discussed in problems R51 of the Rhind papyrus, M4, M7, and M17 of the Moscow papyrus, all of which date to the Middle Kingdom. The R51 problem constitutes in the world history of mathematics, the first written testimony that deals with the calculation of the area of a triangle.
Statement of Rhind papyrus problem R51:
Example of calculation of a triangle of land. If someone says to you: a 10 khet triangle on his mryt and 4 khet base. What's your area? Calculate half of 4, which is 2 to form a rectangle. Multiply 10 by 2. This is your area.
The term mryt probably means height or side. However, the formula used to calculate the area suggests the interpretation in favor of the first solution. The scribe took half of the base of the triangle and calculated the area of the rectangle formed by that side and the height; that is to say
A=base2mrandt{displaystyle A={frac {mathrm {base}{2}}{mathrm {mryt} }}}{equivalent to the common formula used today:
A=bh2{displaystyle A={frac {bh}{2}}}}The fact that a triangle with sides 3-4-5 is a right triangle was also known to the ancient Egyptians and Mesopotamians.
Euclid, in Book I of his Elements , around 300 BC, enunciated the property of the sum of the angles of the triangle.
Contenido relacionado
Thales's theorem
Fundamental Homomorphism Theorem
Logic
































































![{displaystyle [AB]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13e80b9404482bdbe7fe18d8435b3dd42fd39bb0)
![{displaystyle [AC]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49b377aec839d74e0b48a42d2ba192d3efefc575)
![{displaystyle [BC]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd2ee765006b05ac0001c01a206871306f108cbc)






















![{displaystyle [AH]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98621a04b0a0b00e439c7cda9894bf1e184781bf)
![{displaystyle [BH]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2f58a4ff7ecbc9c1f643ed7500daba1612c57b4)
![{displaystyle [CH]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49f6a126a2744c5e2e4a216010592f61ba749447)