Tree (computing)
In computer science and computer science, a tree is a widely used abstract data type (ATD) that mimics the hierarchical structure of a tree, with a value at the root and subtrees with a parent node, represented as a set of linked nodes.
A tree data structure can be defined recursively (locally) as a collection of nodes (starting from a root node), where each node is a data structure with a value, together with a list of references to the nodes (the children), provided that no references are duplicated and no nodes point to the root.
Alternatively, a tree can be abstractly defined as a whole as an ordered tree, with a value assigned to each node. Both perspectives are useful: while a tree can be analyzed mathematically, it is actually represented as a data structure in which each node is worked on separately (rather than as a list of nodes and an adjacency list between nodes, as a graph). Looking at a tree as a set, we can talk about the parent node of a given node, but in general we talk about a data structure of a given node that only contains the list of its unreferenced children. his father (if there is one).
Definition
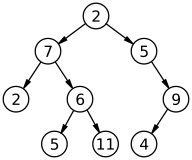
A tree is a (possibly nonlinear) structure of data made up of nodes, vertices, and edges that is acyclic. A tree that has no nodes is called an empty or null tree. A tree that is not empty consists of a root node and potentially many additional levels of nodes that form a hierarchy.
Terminology used in trees
- Raice: The top node of a tree.
- Son: A node connected directly to another when it moves away from the root.
- Father: The reverse notion of son.
- Brothers: A set of nodes with the same father.
- Descendant: A node accessible by repeated descent from father to son.
- Ancestor: A node accessible for repeated promotion from child to father.
- Sheet: A node without children.
- Internal node: A node with at least one son.
- Degree: Number of subtrees of a node.
- Arm: The connection between one node and another.
- Camino: A sequence of nodes and arms connected to a descending node.
- Level: The level of a node is defined by 1 + (the number of arms between the node and the root).
- Height of a node: The height of a node is the number of arms on the longest path between that node and a leaf.
- Height of a tree: The height of a tree is the height of its root node.
- Depth: The depth of a node is the number of arms from the root of the tree to a node.
- Forest: A forest is a set of trees n ≥ 0 disjuntos.
- Rama: A route from the root node to any other node.
Data type vs. data structure
There is a distinction between a tree as an abstract data type and as a concrete data structure, analogous to the distinction between a list and a linked list. As a data type, a tree has a value and children, and the children are themselves subtrees; the value and children of a tree is interpreted as the value of the root node and the subtrees of the children of the root node. To allow trees to be finite, one must either allow the list of children to be empty, or allow trees to be empty, in which case the list of children can be of fixed size (factor of branching, especially 2 or binary), if desired.
As a data structure, a linked tree is a group of nodes, where each node has a value and a list of references to other nodes (its children). This data structure actually defines a directed graph, because it can have loops or multiple references to the same node, just like a linked list. Then there is also the requirement that no two references point to the same node (that each node has at most one parent, and in fact all do, except for the root), and a tree that violates this is treecorrupt.
Due to the use of references to trees in the data structure of a linked tree, trees are often referred to as being implicitly represented by references to the root node, since this is, normally, the way in which they are actually applied. For example, instead of an empty tree, one can have a null reference: a tree is never empty, rather a reference to a tree can be null.
Recursion
Recursively, a tree as a data type is defined as a value (of a certain data type, possibly empty), together with a list of the trees (possibly an empty list), the subtrees of their children:
t: v [t[1], t[k]
(A t tree consists of a v value and a list of other trees.)
More elegantly, through mutual recursion, of which a tree is one of the most basic examples, a tree can be defined in terms of a forest (a list of trees), where a tree consists of a value and a forest (the subtrees of its children):
f: [t[1],..., t[k] t: v f
Note that this definition is in terms of values, and is appropriate in functional language (referential transparency is assumed); different trees are unconnected, as they are simply lists of values.
As a data structure, a tree is defined as a node (the root), which itself consists of a value (of some data type, possibly empty), together with a list of references to other nodes (possibly empty list and possibly null references):
n: v [ strangern[1],..., &n[k]
(An n node consists of a v value and a list of references to other nodes.)
This data structure defines a directed graph, and for it to be a tree, a condition must be added to its global structure (in its topology), and this is that at most one reference can point to any given node (a node has at most one parent), and no node in the tree can point to the root. In fact, all nodes (other than the root) must have exactly one parent, and the root must not have any parents.
In fact, given a list of nodes, and for each node in a list of references to its children, one cannot know whether this structure is a tree or not without analyzing its global structure, as defined below.
Theory of types
As an abstract data type (ADD), the abstract tree type T with values of some type E is defined using the abstract type of forests F (tree list), for functions:
- value: T → E
- son: T → F
- null: () → F
- node: E × F → T
with the axioms:
- value(node(e, f) = e
- son(node(e, f) = f
In terms of type theory, a tree is an inductive type defined by the constructors null (empty forest) and node (rooted tree with given value and children).
Mathematically
Viewed as a whole, a tree data structure is an ordered tree, usually with values attached to each node. Specifically, it is (if non-empty is required):
- A tree rooted against the root (a narrower term is a arborescent), means:
- A directed graph.
- Which undirected graphus underlying is a tree (two vertices are connected by exactly a simple path).
- With a prominent root (a vertex is designated as the root).
- What determines the direction in the arms (arrows pointing out of the root; given an arm, the node from where the arrow points is called the father and the node he points to is called the son).
Along with:
- An ordination in the nodes children of a given node, and a value (of some kind of data) in each node.
Trees often have a branching factor of two child nodes (possibly empty, therefore at most two non-empty child nodes). In these cases we speak of a binary tree.
Allowing empty trees makes some simple definitions a bit more complicated: a rooted tree must not be empty, so if empty trees are assigned the above definition, they instead become a empty tree, or a tree rooted in such a way that.... On the other hand, empty trees are simplified by defining a fixed branching factor: with empty trees, a binary tree is a tree such that each node has exactly two children, each of which is a (possibly empty) tree. Sets of operations in a tree must include the fork operation.
Terminology
A node is a structure that can contain a value or condition, or represent a separate data structure (which can be a tree). Each node in a tree has zero or more child nodes, which are arranged below it in the tree (by convention, trees are drawn from top to bottom). A node that has a child is called the parent node of the child (or parent node). All nodes have at least one parent.
An internal node (also known as a child node or branch node) is any node in a tree that has child nodes. Similarly, an external node (also known as an external node, leaf node, or terminal node) is any node that has no child nodes.
The highest node in a tree is called the root node. Depending on the definition, a tree may be forced to have a root node (in which case no tree would be empty), or allowed to be empty, in which case they do not necessarily have a root node. Being the top node, the root node will not have a parent. It is the node in which the algorithms start, since, as the data structure that it is, it can only be passed from parent to child. Note that some algorithms start at the root, but first visit the leaf nodes (accessing the value of the leaf nodes), and access the root last (i.e., accessing the root's children first)., but only access the value of the root as the last step). All other nodes can be accessed by following arms or links. (In the formal definition, each of these paths is unique.) In diagrams, the root node is conventionally drawn at the top. In some trees, such as mounds, the root node has special properties. Each node in a tree can be viewed as the root node of the subtree rooted at that node.
The height of a node is the length of the longest downward path one leaf from that node. The height of the root is the height of the tree. The depth of a node is the length of the path to its root (ie, its path to the root). This is commonly required in the handling of various self-balancing trees (AVL trees, in particular). The root node has zero depth, leaf nodes have zero height, and a tree with only one node (thus both a root and a leaf) has zero depth and height. Conventionally, an empty tree (tree with no nodes, if they are allowed) has depth and height -1.
A subtree of a tree T is a tree consisting of a node in T and all its descendants in T. Then the nodes correspond to the subtrees (each node corresponds to the subtree of itself and all its descendants) - the subtree corresponding to the root node is the whole tree, and each node is the root node of the subtree that determines it; the subtree corresponding to any other node is called the proper subtree (by analogy to a proper set).
Drawing trees
Trees are often drawn on the plane. Ordered trees can be represented essentially and only in the plane, and are therefore called plane trees, in the following way: if one fixes a conventional order (for example, clockwise), and arranges to the child nodes in that order (first incoming parent arm, then first child arm, etc.), this produces an embedding of the tree in the plane. Conversely, such embedding determines an order of the child nodes.
If one places the root at the top (parents above children, like in a family tree) and places all nodes that are a given distance from the root (in terms of number of edges: the level of a tree) on a given horizontal line, a standard drawing of the tree is obtained. Given a binary tree, the first child is on the left (the left node), and the second child is on the right (the right node).
Representations
There are many different ways to represent trees; the most common representations represent nodes dynamically as records with pointers to their children, their parents, or both, or as elements of an array, with relationships between them determined by their positions in the array (for example, a binary heap).
In fact, a binary tree can be implemented as a list of lists (a list where the values are lists): the head of a list (the value of the first term) is the left child, while the tail (the list of the second and following terms) is the right child. This can be modified to allow values, as in symbolic expression (S-expression) lists, where the head (first-term value) is the value of the node, the head of the tail (second-term value) is the left child, and the tail of the tail (list of succession terms) is the right child.
In general a node in a tree will not have pointers to its parents, but this information can either be included (by extending the data structure to also include a pointer to the vector) or stored separately. Alternatively, the uplinks can be included in the data of the child node, as in a linked binary tree.
Generalizations
Graphs
If arms (to child nodes) are thought of as references, then a tree is a special case of a graph, and the tree data structure can be generalized to represent a directed graph by removing constraints on that a node can only have at most one parent, and that no cycles are allowed. Arms are still considered to be pairs of nodes, however the terms parents and children are generally substituted with different terminology (for example, source and target). There are different implementation strategies: a graph can be represented by the same local data structure as a tree (nodes with value and lists of their children), assuming that "the list of children" either a list of references, or globally by structures such as adjacency lists.
In graph theory, a tree is a connected acyclic graph; Unless otherwise stated, in graph theory, trees and graphs are assumed to be undirected. There is no one-to-one correspondence between such trees and trees as data structures. We can take an arbitrary tree with no direction, and arbitrarily choose one of its vertices as the root, and make all of its arms point away from the root - producing an arborescence - and assign an order to all of them. the nodes. The result corresponds to a tree data structure. Choosing a different root or a different order produces a different graph.
Given a node in a tree, its children define an ordered forest (the union of subtrees given by all its children, or what is equivalent, take the subtree given by the node itself and delete the root). Just as subtrees are fond of recursion (as in a depth search), forests are fond of corecursion (as in a breadth search).
Through mutual recursion, a forest can be defined as a list of trees (represented by root nodes), where a node (of a tree) consists of a value and a forest (its children):
f: [n[1],..., n[k] n: v f
Traversal methods
Passing through the elements of a tree via parent-child connections is called traversing the tree, and the action is a path through the tree. Often, an operation can be performed when a pointer reaches a particular node. A path in which each parent node is traversed before its children is called a preorder path; a path in which the children are traversed before their respective parents is called a post-order path; a path in which a node's left subtree, the node itself, and finally its right subtree are traversed is called a traversal order. (The latter situation, in reference to exactly two subtrees, a left subtree and a right subtree, is specifically a binary tree.) A level-ordered path performs an effective-width search on the entire tree; nodes are traversed level by level, with the root node being visited first, followed by its direct child nodes and its siblings, followed by its grandchild nodes and its siblings, etc., until all nodes in the tree have been traversed.
Common operations
- List all elements
- List the section of a tree
- Find an element
- Add a new element in a certain position of the tree
- Delete an element
- Pod: Delete an entire section of a tree
- Graft: Add an entire section to a tree
- Find the root of some node
- To represent each node as a variable in the mound with pointers.
- Represent the tree with a vector
Common uses
- Representing a hierarchical data
- Store a data so that your search is efficient (see search for binary trees and tree paths)
- Represent orderly data lists
- As a workflow for the composition of digital images
- Coating algorithms
Contenido relacionado
Stress test (computer)
KWin
XHTML