Topology

ImprimirCitar

Illustration of the theorem of the four colors.

The topology (from the Greek τόπος, 'place', and λόγος, 'study') is the branch of mathematics dedicated to the study of those properties of geometric fields that remain unchanged by continuous transformations. It is a discipline that studies the properties of topological spaces and continuous functions. Topology is concerned with concepts such as proximity, number of holes, the type of consistency (or texture) that presents an object, compare objects and classify multiple attributes where connectivity, compactness, metricity or metrizability stand out, among others.

Mathematicians use the word topology with two meanings: informally it is the meaning specified above, and formally it is the reference to a certain family of subsets of a given set, a family that fulfills certain rules on union and intersection —this second sense can be seen developed in the article topological space—.

Intuitive idea

Colloquially, topology is referred to as the "gum page geometry". This refers to the fact that, in Euclidean geometry, two objects will be equivalent as long as we can transform one into the other through isometries (rotations, translations, reflections, etc.), that is, through transformations that preserve the measures of angle, area, length, volume and others.

In topology, two objects are equivalent in a much broader sense. They must have the same number of pieces, holes, intersections, etc. In topology it is allowed to bend, stretch, shrink, twist, etc., objects, but as long as it is done without breaking or separating what was joined, or gluing what was separated. For example, a triangle is topologically the same as a circle, since we can transform one into the other continuously, without breaking or gluing. But a circle is not the same as a segment, since it would have to be divided (or glued) at some point.

This is why it is called the "rubber page geometry", because it is as if we were studying geometry on a rubber paper that could contract, stretch, etc.

A cup transforming into a doughnut.

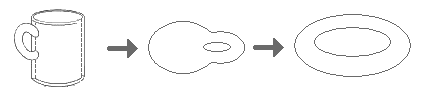
A common joke among topologists (mathematicians who do topology) is that "a topologist is a person who can't tell a cup from a donut." But this vision, although very intuitive and ingenious, is biased and partial. On the one hand, it can lead one to think that topology deals only with geometric objects and concepts, being quite the contrary, it is geometry that deals with a certain type of topological objects. On the other hand, in many cases it is impossible to give an intuitive picture or interpretation of topological problems or even of some concepts. It is common among first-time students to hear that they "don't understand topology" and that they don't like that branch; generally it is because they remain in this graphic attitude. Finally, topology is also largely nourished by concepts inspired by mathematical analysis. It can be said that almost all of the concepts and ideas of this branch are topological concepts and ideas.

A clarifying example

Madrid Metro Plan.

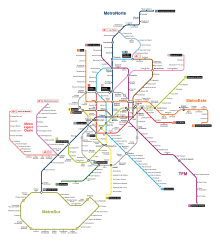
Let's look at a map of the Madrid metro. It shows the stations and the metro lines that connect them, but it is not geometrically exact. The curvature of the subway lines does not match, nor does their length to scale, nor the relative position of the stations... But even so, it is a perfectly useful map. However, this map is exact in a certain sense, since it faithfully represents a certain type of information, the only one we need to decide our way through the metro network: topological information.

History of topology

Historically, the first topological ideas concern the concept of limit and the completeness of a metric space, and they manifested themselves mainly in the crisis of the incommensurables of the Pythagoreans, before the appearance of non-rational real numbers. The first concrete approach to the concept of limit and also to the integral appears in the method of exhaustion of Archimedes. The appearance of mathematical analysis in the XVII century highlighted the need to formalize the concepts of proximity and continuity, and the inability of geometry to deal with this topic. It was precisely the foundation of the infinitesimal calculus, as well as the attempts to formalize the concept of variety in Geometry, that prompted the appearance of topology at the end of the century XIX and early XX century.

The origin of topology is usually dated to Euler's solution of the Königsberg bridge problem in 1735. Indeed, Euler's solution of the problem uses a fully topological way of thinking, and the solution of the problem It brings us to the Euler characteristic, the first invariant of algebraic topology, but it would be very risky and arbitrary to date the appearance of the topology at that moment. The situation is exactly analogous to that of the calculation of the area of the ellipse by Archimedes.

The term topology was first used by Johann Benedict Listing in 1836 in a letter to his former primary school teacher, Müller, and later in his book Vorstudien zur Topologie ('Studies prior to topology'), published in 1847. Previously it was called analysis situs. Maurice Fréchet introduced the concept of a metric space in 1906.

**Chronology**
Year	Development
300 a. C.	Euclides defines the conical sections and studies the regular polyhedrons, one of the most basic forms studied by topologists.
250 a. C.	Archimedes investigates the spiral curves and truncated polyhedrons.
1735 AD.	Leonhard Euler solves the problem of the Königsberg Bridges.
1858	The Germans August Möbius and Johann Benedict Listing independently discover the now-called Möbius band.
1890	Giuseppe Peano applying the definition of Jordan shows that a square filled is also a curve.
Decade of 1920	Pável Urysón and Karl Menger define the concept of curve from topology.

Formal development

A collection of topology terms with their meanings can be found in the Topology Glossary article. Here and now we will limit ourselves to giving some basic notions.

As we have said, the fundamental concept of topology is the "relationship of proximity", which may seem ambiguous and subjective. The great achievement of topology is to give a precise, objective and useful formulation of this concept. To do this we take a reference set $X$ which will be the atmosphere in which we will move, and to which we will call space. We'll take an element. $x$ of $X$ . Space elements are called points, so $x$ will be called a point, no matter what $x$ be a function, a vector, a set, a maximal ideal in a commutative and unitary ring... A subset $V$ of $X$ It will be a environment of $x$ Yeah. $V$ includes an open set $G$ so that $x$ is element of $G$ . What will we understand by open set? Here is the quid of the question: a collection $T$ of subsets $X$ will be said to be a topology about $X$ Yeah. $X$ is one of the elements of that collection, if $varnothing$ is an element of the collection, if the union of elements of the collection results in an element of the collection and if the finite intersection of elements of the collection is also an element of the collection. To the elements of the collection $T$ are called open topology $T$ and the pair $(X,T)$ it is called topological space.

The conditions for $T$ be topology about $X$ are then these:

{displaystyle (1)quad varnothing in T,Xin T}

{displaystyle (2)quad (O_{1}in T,O_{2}in T)Rightarrow (O_{1}cap O_{2}in T)}

{displaystyle (3)quad forall Ssubset T,cup _{Oin S}Oin T}

It may seem strange that from such a highly formal and conjunctistic definition a precise formulation of the concept of proximity is obtained. The first thing to see is that on the same space $X$ different topologies can be defined, thus generating different topological spaces. On the other hand, precisely the way a topology is determined on a set (i.e., the choice of the criterion that allows us to decide whether or not a given set is open) is what will give "visualizable" character or not to that topological space.

One of the easiest ways to determine a topology is by means of a distance or metric, which is only applicable in some cases (although it is true that many of the most intersing cases of topologies in Geometry and Mathematic Analysis can be determined by some distance). A distance over a set $X$ is an application ${displaystyle d:Xtimes Xlongrightarrow mathbb {R} }$ which verifies the following properties:

{displaystyle d(x,y)geq 0}

;

{displaystyle d(x,y)=d(y,x),}

{displaystyle d(x,y)=0,}

Yes and only if

{displaystyle x=y,}

;

{displaystyle d(x,y)leq d(x,z)+d(z,y)}

Whatever. ${displaystyle x,y,zin X}$ .

If we have defined a distance over $X$ We'll say the couple

{displaystyle (X,d),}

It's a metric space. Given a metric space $(X,d)$ , a topology is determined $X$ in which the open assemblies are the subsets $G$ of $X$ such that whatever the point is $x$ of $G$ There is a number $0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ▪0{displaystyle epsilon } 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/568095ad3924314374a5ab68fae17343661f2a71" style="vertical-align: -0.338ex; width:5.205ex; height:2.176ex;"/>$ in such a way that the whole $<math alttext="{displaystyle {yin X:d(x,y){and한 한 X:d(x,and).ε ε !{displaystyle {yin X:d(x,y)epsilon }} <img alt="{displaystyle {yin X:d(x,y)$ is fully included in $G$ . Altogether $<math alttext="{displaystyle {yin X:d(x,y){and한 한 X:d(x,and).ε ε !{displaystyle {yin X:d(x,y)epsilon }} <img alt="{displaystyle {yin X:d(x,y)$ is called open center ball $x$ and radio $epsilon$ and it will be precisely an environment of the point $x$ .

As noted before, unfortunately not all topology comes from a distance, that is, there are topological spaces that are not metric spaces. When a topological space is also a metric space (that is, when given a topology on a set, a distance can be defined on that set such that the topology generated by the distance coincides with the given topology), the topological space is said to be metrizable.. A classic problem in topology is that of determining what conditions a topological space must satisfy in order to be metrizable.

Branches of the topology

Three branches are usually considered:

the general or joint topology,
algebraic topology and
differential topology.

In addition to these three branches, which we could properly say topological, the involvement to a greater or lesser extent in other mathematical disciplines makes many consider functional analysis, measure theory, knot theory (part of low-dimensional topology), the theory of topological groups, etc. Its contribution to graph theory, mathematical analysis, differential equations, functional equations, complex variable, differential geometry, algebraic geometry, commutative algebra, statistics, chaos theory, fractal geometry... It even has direct applications in biology, sociology., etc.

General or set topology

It forms the basis of studies in topology. In it, topics such as what a topological space is or the surroundings of a point are developed.

Fundamental concepts related to the topology of a set

Topology, topological space, open, closed, subspaces

Sea $X$ a whole. ${displaystyle P(X)}$ the whole of their parts. One topology on $X$ It's a set. ${displaystyle Tsubset P(X)}$ to fulfill ${displaystyle Xin T}$ , ${displaystyle varnothing in T}$ Yeah. ${displaystyle A,Bin T}$ then. ${displaystyle Acap Bin T}$ And if ${displaystyle Ssubset T}$ then. ${displaystyle cup _{Gin S}Gin T}$ . To the elements of $T$ they are called open sets. Al par $(X,T)$ is called Topological space. To the elements of $X$ they are usually called Points.

Note that from the first moment we have specified that the set $X$ is any, not necessarily a set of geometric nature. The denomination of space (topological) and of point remains even though $X$ be a set of numbers, functions, differential equations, geometric figures, vectors, sets...

As can be seen, the definition is very formal and general, and the first thing that is observed is that a multitude of different topologies can be given over the same set. That's right. But for now, the concepts of open set in $mathbb{R}$ or $mathbb {R} ^{2}$ or ${mathbb {R}}^{3}$ meet the conditions required to a topology. It is precisely to verify that other families of groups in other non-mechanical sets of nature that share these same properties (as in the set of solutions of a differential equation, or the set of zeros of polynomials with ideal coefficients in a commutative ring, for example) that motivates this definition. Thus we can apply to these sets the same (or similar) topological techniques that we apply to the open of the plane, for example. The situation is similar to that in Álgebra Lineal when it comes from working on $mathbb {R} ^{2}$ or ${mathbb {R}}^{3}$ to work in arbitrary vector spaces.

As it follows, $(X,T)$ It will always represent a topological space.

Linked to the concept of open set is the closed set. A set ${displaystyle Fsubset X}$ it is said to be closed if your compliment ${displaystyle Xsetminus F}$ It's a set. Open. It is important to note that a set that is not open should not necessarily be closed, and a set that is not closed is not necessarily to be opened. Thus, they exist sets that are open and closed at once, as $varnothing$ , and there can be sets that are neither open nor closed.

It is immediate to check that the intersection of closures is a closed set, that the union of a finite amount of closed sets is a closed set, and that $X$ Like $varnothing$ They're closed sets.

Yeah. ${displaystyle Zsubset X}$ , the whole ${displaystyle T_{Z}:={Gcap Z:Gin T}}$ is a topology for $Z$ . It will then be said that space ${displaystyle (Z,T_{Z})}$ That's it. topological subspace of $(X,T)$ .

The notion of a topological subspace arises naturally, and is the analogous concept to that of subgroup in Group Theory or the vector subspace in Linear Algebra.

A property relative to topological spaces is said to be heritable when if a space has it, then so does any of its subspaces.

Basis of a topology, neighborhoods, local bases, countability axioms

A family ${displaystyle {mathcal {(}}B)subset T}$ is said to be base (from topology) $T$ ) if for whatever ${displaystyle Gin T}$ There is a set ${displaystyle Msubset {mathcal {(}}B)}$ so that ${displaystyle G=cup _{Bin M}B}$ .

It's not always comfortable to work with a topology. Sometimes it is more difficult to establish a topology than a topology basis (as in metric spaces). In any case, a base is a very convenient way of establishing a topology. Even easier is to establish a subbase, which is a family of sets for which the set of its finite intersections forms a topology basis. One of the most important cases of topology, that of metric spaces, It is given by a base, that of the set of open balls in space.

A topological space is said to satisfy the Second Axiom of Countability (IIAN) if there exists some basis of its topology that has countable cardinality.

Sea $Asubset X$ any set and $xin A$ an arbitrary point. It's said that $A$ That's it. environment of $x$ if there is an open set ${displaystyle G}$ so that ${displaystyle xin Gsubset A}$ . Every open set is an environment of all its points. To all the environments of a point $x$ is called environment system of $x$ .

Note that a neighborhood is not required to be an open set. open environments are a type of very useful environments (especially in Geometry and Analysis) and widely used, so much so that in many times the qualifier open is omitted. This is an abuse of language and should be avoided.

A collection ${displaystyle {mathcal {(}}V)}$ of environments of one point x is said to be a environment base (o) local base) $x$ if given any environment $V$ of $x$ There is a ${displaystyle Bin {mathcal {(}}V)}$ so that ${displaystyle Bsubset V}$ .

A topological space is said to satisfy the First Axiom of Countability (IAN) if every point in the space has some local countable cardinal basis.

Notable subsets associated with a set

Now we can establish a series of definitions of great importance, since they will be the pieces basics of the study of topology and will constitute the raw material of subsequent concepts.

Interior, exterior, border

A point $xin X$ will be said to be a inner point of $A$ if there is an environment $N$ of $x$ such as ${displaystyle Nsubset A}$ . Thus, the set of inner points to $A$ is an open set, called Interior of A, denoted by Int (A) or also ${displaystyle {stackrel { circ }{A}}}$ . It is the largest open set included in A.

A point ${displaystyle yin X}$ will be said to be a outer point a $A$ if there is an environment $N$ of $y$ such as $N$ ${displaystyle Xsetminus A}$ . Also, the set of outer points to $A$ is another open set, called Exterior of A and denoted by Ext (A).

A point ${displaystyle zin X}$ is said to be a border point of $A$ if all environments $V$ of $z$ It's such that ${displaystyle Vcap Aneq varnothing }$ and ${displaystyle Vcap (Xsetminus A)neq varnothing }$ . To the border point set $A$ is called Border of A and denotes Fr(A). In other words, everything with center in $z$ shall have elements belonging to the whole $A$ and other elements outside the whole $A$ . The border $A$ It's a closed set.

Adhesion, accumulation, isolated points

A point $xin X$ is said to be a accession point of $A$ if all environments $V$ of $x$ It's such that ${displaystyle Acap Vneq varnothing }$ . It is thus evident that every inner point and every border point is a point of adherence. To the set of adhesion points of the set $A$ is called adherence or Closing of $A$ and denotes by ${displaystyle Cl(A)}$ or ${displaystyle {bar {A}}}$ . La closure of a set $A$ is a closed set, and is the smallest enclosed set that contains the set.

A point $xin X$ is said to be a accumulation point of $A$ if all environments $V$ of $x$ It's such that ${displaystyle (Vsetminus {x})cap Aneq varnothing }$ . The assembly of the accumulation points of a set is called accumulation of the whole, or derivative joint, and denotes him for ${displaystyle A^{d}}$ or $A'$ .

A point $xin X$ is said to be a point ${displaystyle Omega }$ -accumulation of $A$ if all environments $V$ of $x$ It's such that ${displaystyle (Vsetminus {x})cap A}$ It's an infinite set. To the set of points $Omega$ -accumulation of a set is called $Omega$ -accumulation of the whole, or group $Omega$ -derived., and denotes him for ${displaystyle A_{Omega }^{d}}$ or ${displaystyle A'_{Omega }}$ . All point $Omega$ -accumulation is build-up point, and all build-up point is point of adherence to the same set.

A point $xin X$ is said to be a isolated point of $A$ if there is any perforated environment $V$ of $x$ (i.e., a set ${displaystyle Vsubset X}$ so that ${displaystyle Vcup {x}}$ is an environment $x$ ) so that ${displaystyle Vcap A=varnothing }$ . To the set of isolated points $A$ is called set of isolated points of $A$ , and denotes him for ${displaystyle A^{a}}$ . All isolated point is border point and is also point of adherence to the same set.

In topology, the inner sets and closure of a set are of paramount importance. Its importance lies in being, respectively, the largest open contained in the set and the smallest closed that contains the set. The interior can also be obtained as the union of all the open ones contained in the set, and the closure as the intersection of all the closed ones that contain the set. Not so important in topology but very important in other areas of Mathematics are the accumulation sets, frontier and isolated points of a set.

Fundamental concepts related to continuous applications and convergence

Convergence

The idea of convergence is to "approximate" one object for another, that is, substituting an object for another that is close to it. Obviously, doing so is making a mistake, a mistake that will generally depend on how close the substituted object is to the surrogate object. In order to do this substitution in a systematic way, so that the error can be chosen arbitrarily small, different types of sets appear. Thus, a process of successive approximations is obtained which, if all goes well, would end up leading us to the object, even after an infinite number of approximations. The simplest of these sets is a sequence, that is, an infinite (countable) and ordered collection of objects, although there are other sets with the same character of order that better reflect the concept of convergence.

It is important to note that the topology does not work with errors or approximations. That falls within the scope of Numerical Analysis and even Mathematical Analysis. What topology does in this problem is provide the basic tools and theoretical concepts to correctly face the problem, always from a conceptual and qualitative point of view. It studies what must be understood when we say that a set (such as a sequence) approaches an object (which can be a point, a set, etc.).

Convergence of sequences

A succession is an application in a set whose domain is the set of natural numbers. In particular, a succession to a topological space ${displaystyle (X,T),}$ is an application ${displaystyle (x_{n})_{nin mathbb {N} }:mathbb {N} longrightarrow X}$ .

A sequence is the simplest case of infinite domain application.

It's said that $xin X$ It's a point limit succession ${displaystyle (x_{n})_{nin mathbb {N} }}$ or what? ${displaystyle (x_{n})_{nin mathbb {N} }}$ converge to the point $x,$ if it is fulfilled, whatever the environment ${displaystyle V,}$ of $x,$ There is a natural number $n_0$ so if $n$ is another natural number greater or equal than $n_0$ (I mean, ${displaystyle ngeq n_{0}}$ ) then it is fulfilled that ${displaystyle x_{n}in V}$ .

There are two observations to make about this:

First, the case may be that the succession has no limit points, or even has more than one limit point. To the set of limits of a succession ${displaystyle (x_{n})_{nin mathbb {N} }}$ is called limit of ${displaystyle (x_{n})_{nin mathbb {N} }}$ (and denotes him for ${displaystyle lim _{nin mathbb {N} }x_{n}}$ or also for ${displaystyle ,lim _{nto infty }x_{n}}$ ).
Secondly, the interpretation of this concept is the following: as close as we want from a limiting point we can find all the points of succession, except at most a finite quantity of them (which may or may not be very large, but does not cease to be finite).

A point $xin X$ That's it. agglomeration point succession ${displaystyle (x_{n})_{nin mathbb {N} }}$ if whatever the environment $V$ of $x$ the whole ${displaystyle {nin mathbb {N}:x_{n}in V}}$ It's infinite. Every limit point is a point of agglomeration, but reciprocal is not true. For example, the oscillation limits of an unverging succession of real numbers (such as succession) ${displaystyle (-1)^{n}+{frac {1}{n}}}$ ) are points of agglomeration, but are not limits (there is no limit for such succession, whereas 1 and -1 are points of accumulation).

Application Continuity

Another totally fundamental concept studied in this branch is that of continuous application. An application ${displaystyle f:Xlongrightarrow Y}$ between two topological spaces is said to be continuous if given any set $G,$ open ${displaystyle Y,}$ , the whole ${displaystyle f^{-1}(G)={xin X:f(x)in G}}$ is an open set in ${displaystyle X,}$ .

With the same notation, yes $xin X$ We'll say $f,$ is continuous $x,$ when you get that ${displaystyle ,f^{-1}(V)}$ is an environment $x,$ Whatever the environment $V,$ of $f(x),$ .

It's immediate then to check $f,$ is continuous when and only when it is continuous $xin X$ , whatever this is, that is, when and only when it is continuous at each of the points in your domain.

Informally speaking, a map is continuous if it transforms points that are close to points that are close, that is, if it respects the "closeness relation". This also means that a continuous function does not "break" those that are united and do not "stick" what is separated

Connected sets, path-connected and arc-connected sets

A set is said to be connected if it cannot be expressed as a union of two non-empty open disjoints.

A set $X,$ it is said to be related by paths if all couple of points can join by a path, that is, ${displaystyle ,forall x,yin Xquad exists phi:[0,1]longrightarrow X}$ continue in such a way that ${displaystyle ,phi (0)=x}$ and ${displaystyle ,phi (1)=y}$ . All related road bundles are related, but not all related packages are related by paths (see, for example, the bosom of the topologist).

These outfits are "made in one piece" (the related) or "made in such a way that they do not have totally loose parts" (those connected by roads). Naturally this is just one way of interpreting them. The parts of an assembly (the largest connected subassemblies that the assembly contains) are called "connected components". For example, a handful of sand would be a set in which the connected components are each grain of sand. A broken mirror would be a set in which each piece of mirror is a connected component. An iron ball is a set with only one connected component, that is, a connected set. A grid is also a connected set, formed by a single connected component.

There is another notion of connection, the connection by arcs or arc connection slightly more restrictive than the connection by paths. The path is required to be a homeomorphism on its image. Even so, the connection by arcs and by paths coincide on Hausdorff spaces.

Compactness

Compact sets are a much more difficult type of set to define. A space is compact if for all coverage by open spaces (family of open spaces whose union contains the total space X) there is a finite subcovering (finite family of open spaces, formed only by sets of the previous family, whose union contains X).

In a metric space, a compact set meets two conditions: it is "closed", that is, it contains all its boundary points; and is "bounded", that is, it is possible to draw a ball that contains it, although the converse is not necessarily true. That is, there can be closed and bounded sets that are not compact. Compactness is a very important property in topology, as well as in Geometry and in Mathematical Analysis.

In any topological space, a closed set inside a compact is always compact. Furthermore, in a Hausdorff topological space, a compact is always closed.

Metricization

A topology on a set is metrizable if it is possible to find a distance such that the openings for that distance are exactly the openings of the starting topology. Metrizability is also a very desirable property in a topological space, since it allows us to give a very simple characterization of the topology's open spaces, as well as implying certain other properties.

Separation

Separation properties are certain properties, each one one degree more restrictive than the last, that tell us the "resolution" or "fineness of grain" of a topology. For example, the separation property T2 means that for two distinct points, disjoint neighborhoods can always be found (that is, they do not intersect).

Density

A set is dense in space if it is "close to all points" of that space. More precisely, a set is dense if its topological closure is all of space. Equivalently, a set is dense if its intersection with any non-empty open space is also non-empty. A set is said to be separable if it has some dense and countable subset.

Product topology and quotient topology

The product topology provides us with a way to topology the Cartesian product of several topological spaces in such a way that good properties are preserved, in particular that the projections onto each factor are continuous and open maps. The quotient topology provides us with a way to topology the quotient (class space) of a space by an equivalence relation, so that it has the largest possible number of open sets and yet the projection is continuous (i.e. the reciprocal image of each open is an open).

Algebraic topology

Algebraic topology studies certain properties related to the connection of a space, properties that we could describe as "porosity" of a space, the number of gaps it presents. For this, he uses algebraic instruments, fundamentally group theory and homological algebra, to such an extent that his development is completely algebraic.

In algebraic topology, a great diversity of problems included in knot theory, for example, or in homotopy theory and homology theory, are considered.

To succinctly understand these issues, let's go back to the examples of connected sets. As we have said, a grid, an iron ball or a sponge are connected sets. However, we all understand that it seems that they do not have the same "degrees of connection", to put it in some way. While an iron ball is solid, a sponge and a grid have holes, and it even seems clear that there is a certain difference between them as well. Homotopy and homology address these issues.

Contenido relacionado

Más resultados...