Topological space

Four examples of topologies and two that are not, in the set of three points {1,2,3}.
The lower left example is not a topology because the union {2} and {3}, equal to {2,3}, is not part of the collection.
Neither is the lower right example, because the intersection of {1,2} and {2,3}, equal to {2}, is not part of the collection.

A topological space is a mathematical structure that allows the formal definition of concepts such as convergence, connectivity, continuity, and neighborhood, using subsets of a given set. The branch of mathematics that studies spaces topological is called topology. Manifolds, like metric spaces, are specializations of topological spaces with their own constraints and structures.

History

Around 1735, Leonhard Euler discovered the formula V− − E+F=2{displaystyle V-E+F=2} which relates the number of vertices, edges and faces of a convex polyhedron, and therefore a flat graph. The study and generalization of this formula, specifically by Cauchy (1789-1857) and L'Huilier (1750-1840), led the study of topology. In 1827, Carl Friedrich Gauss published General investigations of curved surfaces, which in section 3 defines the curve surface in a manner similar to the modern topological understanding: "It is said that a curved surface has continuous curvature in one of its points A, if the direction of all the straight lines drawn from A to points of the surface at an infinitely small distance of A deviates infinitely little from the same plane passing through A."

However, "until Riemann's work in the early 1850s, surfaces were always treated from a local point of view (as parametric surfaces) and topological issues were never considered". "Möbius and Jordan seem to be the first to realize that the main problem of the topology of (compact) surfaces is to find invariants (preferably numerical) to decide the equivalence of surfaces, that is, to decide if two surfaces are homeomorphic or not."

The theme is clearly defined by Felix Klein in his "Erlangen Programme" (1872): the geometric invariants of arbitrary continuous transformation, a kind of geometry. The term "topology" was introduced by Johann Benedict Listing in 1847, although he had used the term in correspondence some years earlier in place of "Analysis situs"; previously used. The foundation of this science, for a space of any dimension, was created by Henri Poincaré. His first paper on this topic appeared in 1894. In the 1930s, James Waddell Alexander II and Hassler Whitney first expressed the idea that a surface is a topological space that is locally like a Euclidean plane.

Topological spaces were first defined by Felix Hausdorff in 1914 in his seminal "Principles of Set Theory". Metric spaces had previously been defined in 1906 by Maurice Fréchet, although it was Hausdorff who popularized the term "metric space" (in German, metrischer Raum).

Definition

Formally, the ordered pair (X,T) formed by a set X and a topology T on X is called topological space, that is, a collection of subsets of X that satisfy the three properties following:

1. The empty set and X They're in. T.

   ∅ ∅ 한 한 T,X한 한 T{displaystyle quad varnothing in T,Xin T}

2. The intersection of any finite subcollection of sets of T It's in. T.

   (O1한 한 T,O2한 한 T)⇒ ⇒ (O1 O2한 한 T){displaystyle quad (O_{1}in T,O_{2}in T)Rightarrow (O_{1}cap O_{2}in T)}

3. The union of any subcollection of assemblies T It's in. T.

This condition is also written, formally:

Русский Русский S T, O한 한 SO한 한 T{displaystyle textstyle quad forall Ssubset T,bigcup _{Oin S}Oin T}

The sets belonging to the topology T are called open sets or simply open sets of (X,T); and their complements in X, closed sets.

Examples

• La trivial topology or indiscreet: is formed by ∅ ∅ {displaystyle varnothing } and X{displaystyle X}.
• La discreet topology: is formed by the whole of the parts X{displaystyle X}.
• La topology of finite accessories: is formed by ∅ ∅ {displaystyle varnothing } and sets of X{displaystyle X}whose supplements are finite.
• La topology of numberable add-ons: is formed by ∅ ∅ {displaystyle varnothing } and sets of X{displaystyle X}, whose complements are numberable.
• Given a subset A X{displaystyle Asubset X}, the collection of subsets {∅ ∅ ,A,X!{displaystyle {emptysetA,X}} It's a topology in X.
• R, set of the reals, and T the set of open intervals in the usual sense, and meetings (any) of open intervals. In this case a set is open if for any point of it there is an open interval that contains the point and that open interval is fully contained in the aforementioned set.
• Sorgenfrey Recipe: the real straight along with the topology of the lower limit.
• La Sierpinski topology is the collection T = { ∅, {0}, x} over X = {0.1} and the pair (X,T) is called Sierpinski space.
• A topology T over X, using some parts of A, which is part of X. The pair (X,T) is a topological space whose open are certain parts of A and the X set. For this case, X = {a,b,c,d}; A ={a,b,c}; T = {∅,{a}, {a,b}, {a,b,c}, X} is a topology on X.

Metric-induced topology

In all metric space (X,d) you can naturally define a topology given by the metric of space. In this topology, called metric topology, open sets are arbitrary open ball joints: the open center ball p한 한 X{displaystyle pin X} and radio r{displaystyle r} is the set of points X that are at a distance d of p{displaystyle p} strictly lower than r{displaystyle r}

<math alttext="{displaystyle quad B(p,r)={qin Xmid d(p,q)B(p,r)={q한 한 X d(p,q).r!.{displaystyle quad B(p,r)={qin Xmid d(p,q) ingredientr}. !<img alt="{displaystyle quad B(p,r)={qin Xmid d(p,q)

Metric topology generalizes the usual notion of an open set on the real line and in 2- or 3-dimensional Euclidean spaces, allowing a local approach to topology.

Instead of considering the whole set, the local point of view consists in asking: what relation must there be between a point to any of A, and A for A to be an open?

If one considers the best-known example, that of intervals, one realizes that open intervals are those that do not contain points on their frontier or edge, which are points in contact with both A and its complementary R - A.

In other words, a point of an open is not directly in contact with the "outside".

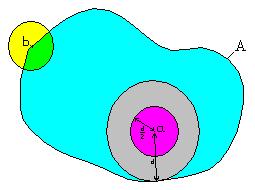
Not being in contact intuitively means that there is a certain distance between the point and the exterior; let's call it d. Then ball B (a, d/2), with radius d/2 and center a, is included in A and does not touch the complementary ball. In the figure, a is in the interior of A, while b is on its boundary, because any neighborhood of b finds R - A.

Not all topologies come from a metric: there are spaces that are metrizable and others that are not. The Nagata-Smírnov Theorem, among others, allows us to determine if a topological space is metrizable or not.

Topology is intended to abstract familiar concepts from metric spaces, but without reference to a distance. For this reason, the concept of open ball is replaced by the more general one of environment or neighborhood. A neighborhood of a point x is this point with something around it. There is some freedom in defining the meaning of "around" and "neighborhood" in order to satisfy the following axioms:

1. x belongs to all its neighbours.
2. A set containing a x-neighbourhood is a x-neighbourhood.
3. The intersection of two x-neighbourhoods is also a x-neighbourhood.
4. In all V neighbourhoods of x there is another U neighborhood of x such that V is a neighborhood of all points of U.

We call open a set that is a neighborhood for all its points.

The axioms stated in the global point of view are verified:

1. E is obviously a neighbourhood for all points, and ∅ also because it contains no point. (A universal property: for all x... is necessarily true in the empty set.)
2. An open union O_i is a superset of each O_iand O_i is a neighborhood of all its points, therefore the union is a neighborhood of all its points, thanks to the property (2).
3. Be x a point of intersection of the open O₁ and O₂. O₁ and O₂ are open that contain x and therefore his neighbors. An intersection of neighbourhoods x It's a neighborhood. x (property 3), which means O₁ {displaystyle cap } O₂ It is a neighborhood of all its points, and therefore an open one.

Properties of a topological space

• Compatibility
• Connectivity
• Separation axioms