Tide

ImprimirCitar

Pleamar views (highland) and low seas (low-summer) in the port of La Flotte on the island of Ré (France) in the Gulf of Vizcaya.

The tide is the periodic change in sea level produced mainly by the forces of gravitational attraction exerted by the Sun and the Moon on the Earth. Although this attraction is exerted on the entire planet, both in its solid, liquid and gaseous parts, we will refer in this article to the attraction of the Moon and the Sun, together or separately, on the waters of the seas and oceans (see also tide of planet Earth).

Other occasional phenomena, such as winds, rains, river overflows and tsunamis cause local or regional variations in sea level, also occasional, but cannot be classified as tides, because they are not caused by force gravitational nor do they have periodicity.

History

The phenomenon of tides has been known since ancient times. It seems that Pytheas (4th century BC) was the first to point out the relationship between the amplitude of the tide and the phases of the Moon, as well as their periodicity. Pliny the Elder (23-79) in his Naturalis Historia correctly describes the phenomenon and thinks that the tide is related to the Moon and the Sun. Much later, Bacon, Kepler and others tried to explain that phenomenon, admitting the attraction of the Moon and the Sun. But it was Isaac Newton in his work Philosophiae Naturalis Principia Mathematica ("Mathematical Principles of Natural Philosophy", 1687) who gave the accepted explanation of the tides at the moment. Later, Pierre-Simon Laplace (1749-1827) and other scientists expanded the study of the tides from a dynamic point of view.

Terminology

Marea vivo en Wimereux, en el Paso de Calais (France).

Marea low in Combarro (Pontevedra, Spain).

Main article: Earth Marea

The following are the main terms used in the description of the tides:

High seas or pleamar: moment when the sea water reaches its maximum height within the tide cycle.
Low or lowmar: opposite moment, when the sea reaches its lowest height.

The approximate time between a high tide and a low tide is six hours, completing a cycle of twenty-four hours and fifty minutes (two high tides and two low tides).

Flow: the flow is the process of slow and continuous ascent of marine waters, due to the progressive increase of lunar or solar attraction or of both attractions in the case of new moon and full moon.
Reflux: the reflux is the process of descending the marine waters, slow and progressive, due to the decrease of the lunar or solar attraction.
Easiness of tide: height difference between folding and lowering (also called tide race.
Micromareal range: when the tide width is less than two meters.
Mesosome Real Rank: when the width or tide race is between the two meters and the four meters.
Macroma Real Rank: when the width or tide race is greater than four meters.
Semiperiod of tide: difference in time between folding and lowering.
Tide stew: is the time when the level stays fixed in the pleamar or in the lowering.
Current stew: is the moment when the current associated with the tide is overturned.
Establishment of the port: is the existing defase, due to the inertia of the hydroosphere, between the passage of the Moon by the meridian of the place and the appearance of the next pleamar.
Age of the tide: is the existing defase, for the same reason, between the passage of the Moon filled by the meridian of the place and the maximum monthly pleamar.
Height unit: average for nineteen years (nodal cycle or cycle meth) of the two maximum tide races (equinoxes) of each year of the cycle.
Living body, tall or sizigia: are the tides that occur with the full moon and the new moon, when the Sun, Moon and Earth are aligned. La Marea Viva which occurs during the new moon phase is called "Marea Viva de Conjunción"; and that which occurs while the full moon phase takes place is called "Living Marea of Opposition".
Dead body, low or square: are the tides that occur during the phases of Crescent room and FourthWhen the positions of the Earth, the Sun and the Moon form an apparent 90° angle.
Cutidal lines: Cotidal lines Tide: tide) are the lines that unite the points in which the pleamar is simultaneous.
Amphidromy Points or amphidromy points: are areas to which the cotidal lines converge and in which the amplitude of the tide is zero.
Port pattern: are the geographical points for which the prediction of date and tide height is calculated and published.
Secondary port: they are geographical points of interest to the navigator but they do not have published a tide prediction calculation, but a correction as to the hour and height that refers to a pattern port and through which the tide data can also be determined.
Tide tables: are the annual publications with the daily prediction of tide heights. They provide, among other data, date, time and tide height for different points along the seashore.

Physical phenomenon of tides

The full explanation of the tidal mechanism, with all the periodicities, is extremely long and complicated. So we will start using all possible simplifications and then get closer to reality by removing some of these simplifications.

The Earth will be considered to be a sphere without continents surrounded by a hydrosphere and revolving around the Sun in an elliptical path without rotating on its axis. For now the Moon will not be taken into account.

When one body is in orbit around another, the force of gravitational attraction between the two is given by Newton's law of gravitation:

F_{g}=Gtextstyle {M_{1}M_{2} over d^{2}},

where:

$scriptstyle {G=6{,}67,10^{{-11}}{Ncdot m^{2} over kg^{2}}}$ is the constant of universal gravitation.
$scriptstyle {M_{1}}$ and $scriptstyle {M_{2}}$ are the masses of the two bodies.
$scriptstyle {d}$ is the distance between the mass centers of the two stars.

This force of attraction is the centripetal force that makes the star describe a circumference.

F_{c}=M_{2}omega ^{2}R_{1}=Gtextstyle {M_{1}M_{2} over d^{2}},

where:

$scriptstyle {M_{2}}$ It's the mass of the star.
$scriptstyle {omega ={2pi over T}}$ is the angular speed of the star and $scriptstyle {T}$ his orbital period.
$scriptstyle {R_{1}}$ is the distance between the mass center of the star and the center of rotation, which coincides with the mass center of the two stars. If the other star is much more massive ( $<math alttext="{displaystyle scriptstyle {M_{1}<M1;M2{displaystyle scriptstyle {M_{1} implies M_{2}}}}}<img alt="scriptstyle {M_{1}<$ ), the center of rotation is very close to the mass center of the massive and $scriptstyle {R_{1}simeq d}$ . This is the case with the Earth and the Sun.

La fuerza de atracción asociada a la órbita y al período solamente se ejerce sobre puntos situados a la misma distancia que el centro de masas. Las zonas más lejanas están menos atraídas y las más cercanas lo están más.

The value of gravity acceleration due to the Sun is exactly what corresponds to an orbit with the angular speed $scriptstyle {omega }$ and with the Earth mass center at a distance $scriptstyle {d}$ from the Sun. All parts of the Earth have the same angular speed around the Sun, but they are not at the same distance. Those that are farther from the mass center will be subjected to a lesser acceleration of gravity and that which are at a lower distance, to a greater acceleration.

There is another force, of the same order of magnitude, due to the fact that the attractive forces converge towards the center of the Sun, which is located at a finite distance. It will be described later.

Some sources make the mistake of adding centrifugal accelerations. If you choose to use an inertial reference system (immobile with respect to the stars), centrifugal forces should not be taken into account, which are fictitious forces and only appear in accelerated reference systems. An observer on Earth sees centrifugal forces because the Earth is in free fall towards the Sun. On the other hand, for a stationary outside observer, only the real forces exist, such as the attractive force that constitutes the centripetal force.

The result of this small imbalance of forces is that the water in the oceans on the opposite side from the Sun feels a force that pushes it towards the outside of the orbit, while the water on the side facing the Sun she feels a force that pushes her towards said star. The consequence is that the sphere of water that covers the Earth is slightly elongated and becomes an ellipsoid of revolution whose major axis is directed towards the Sun. It will be seen that this relative elongation is very small: of the order of one in ten million..

Solar Tides

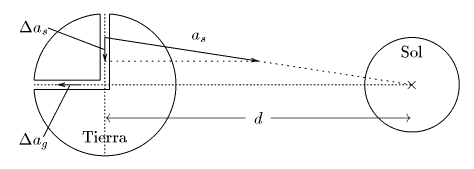To calculate the breadth of solar tides, two imaginary wells are built from the surface to the center of the Earth. One is parallel to the straight that unites the Earth and the Sun and the other is perpendicular.

The strength and acceleration of the water in the perpendicular well are almost parallel to the Earth-Sol axis, but not exactly. The reason is that the Sun is at a finite distance and the forces are directed towards the center of the Sun and are not completely parallel. Let's calculate the perpendicular gravity acceleration component to the Earth-Sol axis, $scriptstyle {Delta a_{s}}$ which experiences the water located at a distance $scriptstyle {r}$ from the center of the Earth. Without more than projecting the acceleration vector, you get to:

textstyle {Delta a_{s} over a_{s}}={r over d}

Here, $scriptstyle {a_{s}}$ is the acceleration due to the attraction of the Sun:

a_{s}=Gtextstyle {M_{s} over d^{2}}

In this last formula, $scriptstyle {M_{s}=1{,}987,10^{{30}}kg}$ is the mass of the Sun and $scriptstyle {d=150,10^{9}m}$ is the distance from Earth to the Sun. For its part, the perpendicular component to the axis remains:

Delta a_{s}=Gtextstyle {M_{s} over d^{2}}textstyle {r over d}

This acceleration varies linearly between the center of the Earth and the surface. The average value is obtained by replacing $scriptstyle {r}$ for $scriptstyle {R over 2}$ Where $scriptstyle {R=6{,}366,10^{6}m}$ It's Earth's radio. This acceleration adds an additional "weight" to the well water column and makes the pressure at the bottom increase a quantity $scriptstyle {rho overline {Delta a_{s}}R}$ Where $scriptstyle {rho }$ It's water density. This increased pressure, transmitted to the ocean surface, corresponds to a variation $scriptstyle {h}$ of the ocean level given by the formula $scriptstyle {P=rho gh}$ (where) $scriptstyle {g=9{,}81m/s^{2}}$ is the acceleration of terrestrial gravity):

h=Gtextstyle {{M_{s} over d^{3}}{R^{2} over 2g}}

Numerical calculation gives a variation of 8.14 cm.

The decrease will now be calculated $scriptstyle {Delta a_{g}}$ of gravity acceleration caused by the Sun at a point located at a distance $scriptstyle {r}$ from the center of the Earth. Adding this additional distance in the gravitational acceleration formula:

a_{g}=Gtextstyle {M_{s} over (d+r)^{2}}=Gtextstyle {M_{s} over d^{2}+2rd+r^{2}}=G{M_{s} over d^{2}left(1+2{r over d}+left({r over d}right)^{2}right)}simeq Gtextstyle {M_{s} over d^{2}}left(1-2textstyle {r over d}right)

The first sum corresponds to the acceleration for a body located at a distance $scriptstyle {d}$ . Therefore, the decrease of acceleration is:

Delta a_{g}=Gtextstyle {M_{s} over d^{2}}2textstyle {r over d}

In turn, the average acceleration is:

overline {Delta a_{g}}=Gtextstyle {M_{s} over d^{3}}R

The pressure variation is, as in the previous case, $scriptstyle {rho overline {Delta a_{g}}R}$ , so:

h=Gtextstyle {M_{s} over d^{3}}textstyle {R^{2} over g}

This acceleration gives an increase in the height of the ocean of 16.28 cm.

With the sum of the two effects, the semimajor axis of the ellipsoid is 24.4 cm greater than the semiminor axis. As the Earth rotates, a point located on the equator sees the height of the sea reach a maximum (high tide) twice a day: each time that point passes through the semimajor axis. In the same way, each time the point passes through a semi-minor axis, the height of the sea passes through a minimum (low tide). The difference between high tide and low tide is 24.4 cm. But we must not forget that this is only the part due to the Sun, that there are no continents and that the inclination of the Earth's axis of rotation has not been taken into account. The variation of the sea height can be approximated by a sinusoid with a period of 12 hours.

Moon Tides

The Moon revolves around the Earth, but the latter is not moving. In fact, both the Moon and the Earth revolve around the mass center of the two stars. This point is approximately 4,670 km from the center of the Earth, measured in the place of the earth's surface that moves from west to east with the lunar translation movement, where the attraction of our satellite is greater at a given time. As the average radius of the Earth is 6,367,5 km, the mass centre is about 1700 km deep beneath its surface. The Moon has a mass $scriptstyle {M_{ell }=7{,}349,10^{{22}}}$ kg and is at an average distance from Earth $scriptstyle {d_{ell }=3{,}84,10^{8}}$ m. The calculation of lunar tides is similar to the calculation of solar tides. Just replace the mass and distance of the Sun with the Moon. The height difference of the ocean due to non-parallelism of the forces is:

h=Gtextstyle {{M_{ell } over d_{ell }^{3}}{R^{2} over 2g}}

Numerical calculation gives us a variation of 17.9 cm.

The difference in height of the ocean caused by the difference in attraction due to the different distances from the Moon is:

h=Gtextstyle {{M_{ell } over d_{ell }^{3}}{R^{2} over g}}

Numerical calculation gives us a variation of 35.6 cm.

The difference in longitude between the semimajor axis and the semiminor axis of the ellipsoid due to lunar tides of 35.6 cm. Therefore, the amplitude of the lunar tides is approximately twice that of the solar tides. As for solar tides, the variation in sea height at a point on the Earth's surface can be approximated by a sinusoid. This time, the period is 12 hours, 25 minutes, and 10 s.

Spring Tides and Neap Tides

When the Moon and the Sun are aligned, the ellipsoids (in pointed) are reinforced and the tides are larger. When the Moon is in square with the Sun, the ellipsoids are partially cancelled and the tides are small.

The ellipsoid due to solar tides has its major axis directed toward the Sun. The ellipsoid due to lunar tides has its major axis directed toward the Moon. Since the Moon revolves around the Earth, the major axes of the ellipsoids do not rotate at the same rate. With respect to the stars, the rotation period of the solar ellipsoid is one year. The ellipsoid of the Moon is 27.32 days. The result is that the axes of the two ellipsoids get closer every 14.7652943 days. When the major axes of the two ellipsoids are aligned, the tidal amplitude is maximum and are called spring tides or syzygian tides. This happens on new moons and full moons. On the other hand, when the major axis of each ellipsoid is aligned with the minor axis of the other, the tidal amplitude is minimal. This happens in the waning quarters and the waxing quarters. These tides are called neap tides or quadrature tides.

Tilt of the Earth's axis

Until now, the fact that the Earth's axis of rotation is tilted by about 23.27° with respect to the ecliptic (the plane that contains the orbit of the Earth and the Sun) has been ignored. Also, the plane of the Moon's orbit is inclined about 5.145° with respect to the ecliptic. This means that the Sun occupies positions ranging from 23.44° north of the equatorial plane to 23.44° south of the same plane. The Moon can occupy positions from 28.6° to -28.6°. The consequence of this is that the major axes of the ellipsoids that have been used rarely coincide with the plane of the terrestrial equator.

El Eje mayor del elipsoide de marea está dirigido hacia la Luna. Las dos pleamares diarias, vistas en una latitud de la Tierra, no presentan la misma amplitud.

In the image to the right, point A is at high tide. When the next high tide occurs, 12 hours, 25 min and 10 seconds later, the same point will be found at B. This high tide will be lower than the preceding and subsequent ones.

This diurnal alternation between large and small high tides suggests the sum of two periodicities: one diurnal and the other semi-diurnal. One speaks then of diurnal and semi-diurnal tidal waves, both lunar and solar. This corresponds to a mathematical model and not to physical reality.

Note that point u and the northernmost locations only see one high tide per day. When they should be at the small high tide, they are still on the same side of the ellipsoid. A similar situation occurs in the Southern Hemisphere. Mathematically, the amplitude of the half-day wave is too small for it to create additional highs or lows.

Tides are maximum when the two high tides are equal. That only happens when the major axis of the ellipsoids is parallel to the equatorial plane. That is, when the sun is in the equatorial plane. This occurs during the equinoxes. The equinox tides are the greatest of the year.

Other causes of variation

Several additional factors also contribute to tidal range:

Both the trajectory of the Earth around the Sun, and of the Moon around the Earth, are not circles but ellipses. When the Earth is closer to the Sun (perihelium), the tides are more intense. In the same way, when the Moon is in its perigee, the tides are also larger. The influence of the perigee or apogee of the Moon is ±20 % regarding the average tide.
The larger tides occur in sizigia, that is, when the Sun, Earth and Moon are aligned.
The best alignment of the Sun, Moon and Earth occurs when the Moon passes through the ecliptic between the Earth and the Sun or, what is the same when the Sun is on the lunar node. In that situation, the forces of attraction of the Sun and the Moon are perfectly aligned.
When the Sun is on the equatorial plane, the two daily tides are equal and maximum. That happens in the equinoxes.

Influence of the continents

Cotidal lines (white), amphoric points (white points where the cotidal lines converge) and tide width (in color), with the twisting sense of the pleamar according to the hemisphere.

In the simplified calculation that has been made, in which the Earth has no continents and is covered by a continuous hydrosphere, the distance between the two high tide positions is 20,000 km. The area of ocean whose level is higher than the average value has a diameter of 10,000 km. That distance is greater than the distance between America and Europe or Africa and corresponds to the width of the Pacific Ocean. For an entire ocean like the Atlantic or Pacific to rise in level, its total water content would have to increase. Since the continents prevent this lateral movement of the entire ocean, the semidiurnal wave model does not correspond to reality.

In the image on the right you can see that the height of the oceans does not follow a wave that moves from right to left (towards the West). The displacement of the water and the maxima and minima is much more complicated.

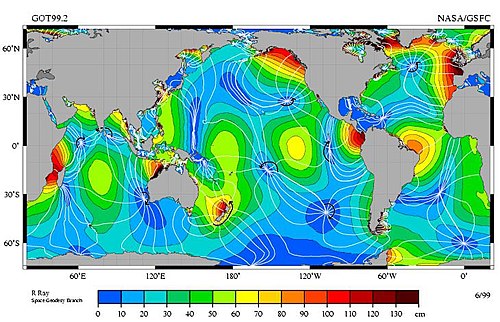
In a model without continents, the cotidal lines coincide with the meridians. In the color image on the right, the cotidal lines of the planisphere are represented and the background color corresponds to the tidal range. These cotidal lines correspond to a particular astronomical situation (crescent moon, equinoxes, etc.) and change over time. In the two images it is observed that there are cotidal lines that converge towards amphidromic points, in which the amplitude of the tide is equal to zero.

The situation is even more marked in the inland seas, whose dimensions are even smaller than those of the oceans. Thus, the Atlantic cannot fill or empty the Mediterranean Sea through the Strait of Gibraltar. The waters of the Mediterranean can only move to the East or to the West, rising at one end and falling at the other. The final result is complicated by the shape of the coasts that limit and divert this lateral movement.

To a greater or lesser degree, all inland seas and open seas (although to a lesser degree) present a circular movement, both in marine currents and in tidal currents and these currents can rotate clockwise at latitudes intertropical northern hemisphere and counterclockwise in the temperate zone of the northern hemisphere. In the case of the southern hemisphere, these rotating movements are reversed, although in this case we cannot speak of seas, but it is the same situation with latitudinal portions of the oceans themselves.

Tides on the coasts

**Great tides**
Locality	Amplitude (m)
Granville, Monte Saint-Michel Bay (France)	13.6
Burntcoat Head, Basin Mines, Fundy Bay (New Scotland, Canada)	11.7
Leaf Lake, Ungava Bay (Quebec, Canada)	9.8
Newport, Bristol Channel (England)	9,2
Sunrise, Turnagain Arm, Cook Inlet (Alaska, USA)	9,2
Río Gallegos (Reduction Beacon) (Argentina)	8.8
Koksoak River Entrance, Hudson Bay, Canada	8.7
Banco Dirección, in the Strait of Magallanes (Chile)	8.5

As we have seen, the tidal amplitude in the high seas is less than 1 meter. On the other hand, near the coasts the amplitude is generally greater and in some cases it reaches or exceeds 10 m. The following table lists some of the places where large tides occur. Only one place per area has been listed.

It is now explained how a tide of less than one meter on the high seas can create a tide of several meters on the coast. The reason is the resonance of the layer of water located on the continental shelf. This layer is shallow (less than 200 m) and, in some cases, extends as far as the continental slope. For example, the English Channel is a layer of water 500 km long (from the entrance to the Pas de Calais), 150 km wide and only 100 m deep. At scale, that corresponds to a body of water 50m long and 1cm deep. When the sea level rises at the inlet, the water enters the English Channel. As the extension is large and the depth is small, the speed of the water increases to about 4 to 5 kn (2 to 2.5 m/s). Reaching that speed takes time (about three hours in the case of the English Channel), but stopping also requires a similar period. Once released, the water continues to advance, spending another three hours until it stops and reverses its direction. The oscillatory behavior is due to inertia and the delay that the water layer has to respond to excitation: the variation in height of the ocean beyond the continental slope. The tide will be larger depending on whether the oscillation period of the area is closer to the period of external excitation, which is 12 hours and 25 minutes.

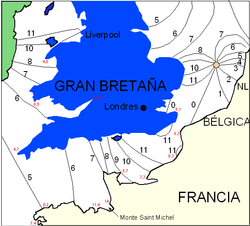
Cotideal lines on the Channel. The numbers in red correspond to the height of large tides according to another reference.

In the image on the left you can see the cotidal lines in the English Channel. The numbers on each line correspond to the delay of high tide with respect to a reference. Note that there is a 6 hour difference between the high tides at the entrance to the English Channel and the Pas de Calais. There are also six hours between the entrance to the English Channel and the Irish Sea (between Ireland and England). There is an amphidromic point (in orange) at the entrance to the North Sea, off the Netherlands.

The oscillation period of the Bay of Fundy in Canada is thirteen hours. As it is very close to the excitation period, the tides are very large. On the contrary, when the proper period moves away from 12.4 h, the tidal amplitudes are smaller. The proper oscillation period depends on the shape of the coast and the depth and length of the continental shelf.

Tides in the equatorial zone

In the areas close to the terrestrial equator, the tides are usually very weak, almost imperceptible, except at the mouths of the rivers, where the rise of sea waters can give rise to the damming of fluvial waters, producing a river surge up when the crests of the incoming tide break against the water of the rivers. This wave produces a characteristic noise that is called bore in the Orinoco delta and pororoca in the Amazon river.

The reason for the low amplitude of the tides in the intertropical zone is due to the fact that it is the area where the effects of the movement of the Earth's rotation are greater due to the centrifugal force generated by said movement. Due to the centrifugal force, the sea level is much higher at the equator than in the temperate zones and, above all, in the polar ones. As is obvious, the greater height of the equatorial waters due to the centrifugal force prevents the tides from being clearly noticeable since this centrifugal force is exerted equally on the entire equatorial circumference while the tides only increase that level where the passage of the Moon and the Sun meet, and it is a much lower level increase.

Tidal currents

As has been said, the variation in sea level on the continental platform requires an alternative movement of water towards the coast and towards the sea. Since the depth of the water is not the same when the tide rises as when it falls, the shape of the obstacles is not the same, and the direction and speed of the current are not the same either. The velocity vector draws a kind of ellipsoid whose major axis is more or less parallel to the coast.

In places where the tides have great amplitude, the speeds of the sea can also be very great. For example, in the English Channel, in the Raz de Sein (in the extreme west of Brittany, in France) and in the Raz Blanchard (in the north of the Cotentin peninsula, also in France), the current exceeds 10 knots (18 km/h) during high tides. In the Strait of Messina, the current can reach 5 knots.

Tidal power stations

Old tidal mill in Isla Cristina (Huelva).

Main article: Maremotriz energy

Tidal power has been used since the Middle Ages in England, France, Spain and probably other countries. The tidal mills of that time only worked at ebb. These, like many other hydraulic mills, fell out of use with the advent of electric motors.

The installation of a tidal power plant creates significant environmental problems such as silting up the river, changes in salinity in the estuary and its surroundings, and changes in the ecosystem before and after the installations.

Earth tides

The forces of gravity that cause the tides of the oceans also deform the Earth's crust. The deformation is important and the amplitude of the terrestrial tide reaches about 25 to 30 cm in syzygy and almost 50 cm during the equinoxes.

Atmospheric tides

Main article: Atmospheric sea

Since atmospheric air is a fluid, as is the case with oceanic waters, the dimensions of the atmosphere also suffer from the action of the tides, affecting its thickness and height and, consequently, atmospheric pressure. Thus, the atmospheric pressure decreases considerably during the full moon and new moon phases, as the air column is attracted by the passage, combined or not, of the moon and the sun through the zenith and/or nadir. As we have seen with ocean tides, the sea level can rise or fall several meters every day in the most favorable places (estuaries or bays). But in the case of the atmosphere, its level can be modified by the attraction of the moon and the sun in several km. It must be taken into account, however, that the atmosphere is thicker in the equatorial zone in particular and in the intertropical zone in general, due to the centrifugal force of the movement of the earth's rotation, so that the intensity of the tides would come to superimposed on said centrifugal force and, as happens with oceanic tides in the intertropical zone, its effects are not so noticeable since they are masked by said centrifugal force. On the other hand, it must be taken into account that the increase in the thickness of the atmosphere due to solar and/or lunar attraction contributes to the decrease in pressure, to the decrease in the speed of the winds (hence the term equatorial calms). which, even though it is correct, has been falling into disuse) and the increase in condensation and rain.

In the intertropical zone, changes in atmospheric pressure during atmospheric tides give rise to remarkable temperature changes that can be seen with a simple thermometer and that would not be explained in any other way: on a full or new moon, for example, can easily rise a degree or more near noon or midnight and in the latter case it would be inexplicable if we did not take into account heating by condensation as the air pressure decreases and rises. Not only the atmospheric pressure is modified with the atmospheric tides, but also the intensity of the rains. A meteorological study for the month of October 2012 would show us a high correlation between the lunar phases with the greatest intensity of hurricanes (Nadine, Rafael and Sandy) and/or their dissipation. In the latter case, the severe flooding caused by Sandy in New Jersey and New York resulted from the combination of the intense tide produced by the full moon (on October 29) and the swell produced by the hurricane itself as it entered the coast of these states, a factor explained in an article from the NHC (National Hurricane Center) whose reading is very appropriate for understanding this topic:

Storm arises is an abnormal rise of water generated by a storm, over and above the predicted astronomical tides. Storm arise should not be confused with storm tide, which is defined as the water level rise due to the combination of storm surge and the astronomical tide. This rise in water level can cause extreme flooding in coastal areas particularly when storm surge coincides with normal high tide, resulting in storm tides reaching up to 20 feet or more in some cases.
A sea of leva (or deep sea) is the abnormal rise of the sea level generated by the waves of a cyclic storm, without taking into account the astronomical tides. A sea of leva should not be confused with a storm tide (galerna) that is defined as the rise of the sea level due to the combination of a sea of leva with the pleamar of an astronomical tide. This rise in sea level can cause extreme floods in coastal areas, particularly when the two causes coincide in the same place, at the same time, being able to reach a wave of about 5 meters high or more in some cases
NHC (National Hurricane Center): Storm Surge Overview

(Taken from Storm Surge Overview article [1])

Slowing down the Earth's rotation

Both the deformation of the Earth due to terrestrial tides and the movement of water from aquatic tides are processes that dissipate energy. The work is done by the moment that the Moon and Sun exert on the deformed part of the Earth and the oceans. The dissipation of energy requires that the major axes of the ellipsoids of the hydrosphere and the Earth are not perfectly aligned with the Moon and the Sun, but have a small phase lag. In the model without continents, this delay would correspond to 3° (and 12 minutes in time). That moment slows down the rotation of the Earth and the length of the day increases by 17 microseconds per year (approximately 1 second every 59,000 years).

The Earth exerts the same momentum on the Moon that the Moon exerts on the Earth. The momentum that the Earth exerts on the Moon gives it energy. Since the Moon is in orbit around the Earth, this increase in energy translates into an increase in the distance between the two stars and an increase in the length of the lunar month. The Earth-Moon distance is increasing by about 38 mm per year.

In the same way that the Moon creates tides on the Earth, both water and land, the Earth also exerts tides on the Moon. The friction due to these tides slowed down the rotation of the Moon, causing it to always present the same face towards the Earth. This fact was interpreted as the possible terrestrial origin of our satellite: being the Earth still a semi-fluid or incandescent body, the rotation movement would have produced a bulge that would increase in speed due to the increase in centrifugal force. Over time, the two stars would have separated, keeping the same lunar face visible from Earth (a currently discredited theory). On other satellites of the solar system that are still rotating, the energy dissipated by the deformations due to the tide generates volcanic activity.

Contenido relacionado

Más resultados...