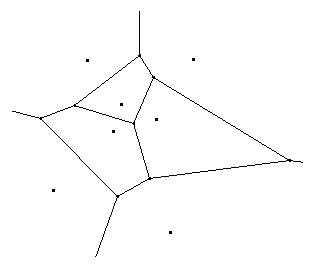
Thiessen polygons

ImprimirCitar

20 points on the plane and its partition of the plane in Voronoi regions.

The Thiessen polygons, named after the American meteorologist Alfred H. Thiessen, are a geometric construction that makes it possible to construct a partition of the Euclidean plane. These objects were also studied by the Ukrainian mathematician Gueorgui Voronoi in 1907, from which they take the alternative name Voronoi Diagrams or Voronoi Tessellation, and by the German mathematician Gustav Lejeune Dirichlet in 1850, from which they take the name Dirichlet tiling.

Voronoi Diagrams are one of the simplest interpolation methods, based on Euclidean distance, especially appropriate when the data is qualitative. They are created by joining the points together, drawing the perpendicular bisectors of the joining segments. The intersections of these perpendicular bisectors determine a series of polygons in a two-dimensional space around a set of control points, so that the perimeter of the generated polygons is equidistant from the neighboring points and designates their area of influence.

Voronoi diagrams in the Euclidean plane R. 2 {displaystyle mathbb {R} ^{2}}

The easiest and most intuitive way to visualize Voronoi diagrams is through their representation in the Euclidean plane. In the classical literature, it is assumed that there is a set of establishments that you want to place on a certain geographical region in such a way that the locations are as profitable as possible. Therefore, a configuration must be found that allows the number of attracted customers to be the most feasible. The logical assumption indicates that customers would go to the establishment closest to their home and not to those that are very far away. Based on this, the Voronoi diagrams give the configuration desired by the establishments. The Voronoi diagram induces a subdivision of the Euclidean plane (the geographic region) based on a set of sites (the establishments), where each site is associated with one and only one subdivision. Furthermore, each subdivision encompasses all the points closest to the site associated with the remaining sites, this is called a Voronói mapping model.

Formal definition

The four most external sites have associated open Voronói regions characterized by semi-arists.

In the first instance, let us note at the euclidian distance between two points $p$ and $q$ for ${displaystyle |p-q|}$ . In the plane then you have:

${displaystyle |p-q|={sqrt {(p_{x}-q_{x})^{2}+(p_{y}-q_{y})^{2}}}}$

Construction of the Voronói region of a site due to the intersection of semi-planes.

Sea ${displaystyle P={p_{1},p_{2},dotsp_{n}}}$ the whole $n$ different points in the plane that are called sites. The Voronoi diagram is defined $P$ as the subdivision of the plane in $n$ regions, one for each ${displaystyle p_{i}in P}$ , fulfilling the proximity property at which a point $q$ belongs to the region of a site ${displaystyle p_{i}}$ Yes and only if $<math alttext="{displaystyle |q-p_{i}| q− − pi . q− − pj {displaystyle intq-p_{i}{i}{i}possible}{intq-p_{j}{j}int}}<img alt="{displaystyle |q-p_{i}|$ for each ${displaystyle p_{j}in P,jneq i}$ . It will be denoted to the Voronói diagram $P$ through ${displaystyle Vor(P)}$ . Each region that corresponds to a site ${displaystyle p_{i}}$ it will be denoted ${displaystyle {mathcal {V}}(p_{i})}$ and it will be called Voronói region ${displaystyle p_{i}}$ .

The region of Voronói for a site ${displaystyle p_{i}}$ is built from the intersections of the semi-planes formed when drawing the bisectors ${displaystyle p_{i}}$ towards the sites ${displaystyle p_{j},jneq i}$ . Taking the case where there are only two sites $p$ and $q$ , traces the straight segment ${displaystyle {overline {pq}}}$ and subsequently the bisector of ${displaystyle {overline {pq}}}$ . This bisector leaves the plane in two semi-planes, where the semi-plane containing a $p$ (represented as ${displaystyle h(p,q)}$ ) represents the geometric place of all the points closest to $p$ to $q$ and the semi-plane containing a $q$ ( ${displaystyle h(q,p)}$ ) hosts all the points closest to $q$ to $p$ . According to this, then you can generally establish how the Voronói region is defined for a site ${displaystyle p_{i}}$ .

${displaystyle {mathcal {V}}(p_{i})=bigcap _{j=1,jneq i}^{n}h(p_{i},p_{j})}$

${displaystyle {mathcal {V}}(p_{i})}$ is composed of the intersection of $n - 1$ semi-planes that make up a convex polygonal region that can be opened or closed. The region is sheltered by a maximum of $n - 1$ vertices and a maximum of $n - 1$ Aristas. They have these amounts of vertices and edges because the most distant sites usually have associated regions of Voronói not sheltered by edges and semi-arists (arists who have a starter vertex but not a final one).

Properties

Below are a set of properties of the Voronói Diagram where it is assumed that there can be no four points of the original set $P$ in a cocircular position. In case this situation is not contemplated, then a lot of details should be considered that should be added to the different properties.

Theorem 1. Sea $P$ a set of $n$ sites on the plane. If all the sites are colinear, then ${displaystyle Vor(P)}$ consists of $n - 1$ parallel lines. Otherwise, ${displaystyle Vor(p)}$ is related and its edges could be segments or semi-lines.
Theorem 2. Stop. ${displaystyle ngeq 3}$ , the number of vertices in the Voronói diagram of a set of $n$ places in the plane is the most ${displaystyle 2n-5}$ and the number of edges is the most ${displaystyle 3n-6}$ .

The following property helps characterize the vertices and edges that make up the Voronói diagram. However, it is necessary to define what the largest empty circle means. $q$ , denoted as ${displaystyle C_{P}(q)}$ . For a point $q$ , ${displaystyle C_{P}(q)}$ is defined as the largest circle you have to $q$ as its center and contains no other site $P$ inside.

Theorem 3. For a Voronoi diagram Vorr(P){displaystyle Vor(P)} ${displaystyle Vor(P)}$ of a set of sites P{displaystyle P} $P$ the following is fulfilled:
- A point $q$ It's a vertex. ${displaystyle Vor(P)}$ Yes and only if your biggest circle is empty ${displaystyle C_{p}(q)}$ contains three or more sites in your contour.
- The bisector between the sites ${displaystyle p_{i}}$ and ${displaystyle p_{j}}$ defines an arist of ${displaystyle Vor(P)}$ Yeah and only if there's a point $q$ on the bisector ${displaystyle C_{p}(q)}$ contains both a ${displaystyle p_{i}}$ and ${displaystyle p_{j}}$ in his contour but not another place.
Theorem 4. Every neighbor closest to the site ${displaystyle p_{i}}$ in $P$ defines an arist of ${displaystyle {mathcal {V}}(p_{i})}$ .
Theorem 5. The region of Voronói ${displaystyle {mathcal {V}}(p_{i})}$ is open if and only if ${displaystyle p_{i}}$ is a point in the convex envelope of the whole $P$ .
Theoremium 6. The dual graph of the Voronói diagram defines the triangulation of Delaunay.

Algorithms for the construction of the Voronoi Diagram

Brute force algorithm

A first approach to the construction of the Voronói diagram is to exploit the geometry of each region of Voronói. For every place ${displaystyle p_{i}in P}$ to build its region of Voronói through the explicit calculation of $n - 1$ semiplanes originated due to the bisectors drawn with respect to other sites. The intersection of these will then be computed $n - 1$ to, finally, give origin to ${displaystyle {mathcal {V}}(p_{i})}$ .

This algorithm has many disadvantages of which are described below. In the first instance, the explicit calculation of the semi-planes and their intersection can cause precision problems on the computer generated, evidently, an incorrect version of ${displaystyle Vor(P)}$ . The second drawback involves that there is no immediate information and that you can take advantage of the neighborhood of each site. Finally, since it is the algorithm of an inefficient algorithm, it is not strange to discover that its computational complexity is high. The algorithm is in order ${displaystyle O(n^{2}log {n})}$

Algorithm divide and conquer

This algorithm is based on the algorithm design paradigm divides and beats. Given the problem of building the Voronói diagram for the whole $P$ of sites, now will divide the latter into two subsets $P_1$ and $P_2$ , with approximately the same size, of which you must find your Voronoi diagram independently. Finally, ${displaystyle Vor(P_{1})}$ and ${displaystyle Vor(P_{2})}$ must be united in order to obtain ${displaystyle Vor(P)}$ . However, what reason exists for it to be believed that ${displaystyle Vor(P_{1})}$ and ${displaystyle Vor(P_{2})}$ have some relationship with ${displaystyle Vor(P)}$ ?

In order to answer the last question, it is necessary to define geometric constructions that will be of vital importance.

Definition 1. Given a request ${displaystyle {P_{1}P_{2}}}$ of $P$ I mean, ${displaystyle sigma (P_{1},P_{2})}$ the set of Voronoi edges that are shared by pairs of Voronoi regions ${displaystyle {mathcal {V}}(p_{i}in P_{1})}$ and ${displaystyle {mathcal {V}}(p_{j}in P_{2})}$ .

The collection of edges ${displaystyle sigma (P_{1},P_{2})}$ has the following properties.

Theorem 7 ${displaystyle sigma (P_{1},P_{2})}$ is the set of edges of a subgraphic ${displaystyle Vor(P)}$ with the following properties:

${displaystyle sigma (P_{1},P_{2})}$ consists of cycles and chains of disjoint edges. If a chain has a single edge, this is a straight line; otherwise its two extreme edges are semi-infite rays.
Yeah. $P_1$ and $P_2$ are linearly separated (if more than one point belongs to the line of separation, all these points are assigned to the same set of partition), then ${displaystyle sigma (P_{1},P_{2})}$ consists of a single monotonic chain.

In order to separate $P$ in two subsets you must be ordered with respect to the abcises and take the straight $m$ so that there are two subsets of approximately the same size. In addition, given this choice of separation line, it can be said that $sigma$ to the plane in a left portion ${displaystyle pi _{L}}$ and a right portion ${displaystyle pi _{R}}$ . Based on this, you have the following property:

Theorem 8. Yeah. $P_1$ and $P_2$ are linearly separated by a vertical line $P_1$ to the left and $P_2$ to the right, then the Voronoi diagram ${displaystyle Vor(P)}$ is the union of ${displaystyle Vor(P_{1})cap pi _{L}}$ and ${displaystyle Vor(P_{2})cap pi _{R}}$ .

It is from the last theorem that the initial question about how two Voronoi diagrams of two partitions are linked to generate the Voronoi diagram of the entire set of sites can be answered. The following algorithm establishes the way to calculate the Voronoi diagram using the divide and conquer technique.

Procedure VORONOI DIAGRAM

Step 1. From $P$ in two subsets $P_1$ and $P_2$ , of approximately the same size, by means of the median at the coordinates x.

Step 2. Build ${displaystyle Vor(P_{1})}$ and ${displaystyle Vor(P_{2})}$ recursively.

Step 3. Build the polygon chain $sigma$ separating $P_1$ and $P_2$ .

Step 4. Download all the edges of ${displaystyle Vor(P_{2})}$ to the left $sigma$ . The result is ${displaystyle Vor(P)}$ the Voronoi diagram of the entire diagram.

Fortune's algorithm (line sweep)

Inspiration

The previously revised raw force algorithm has a complexity ${displaystyle O(n^{2}log {n})}$ However, due to theorem 2, it can be assumed that there is a much more efficient way to find the Voronoi diagram because its constituent elements have complexity $O(n)$ . Indeed, there is this algorithm and it is called Algorithm of Fortune in honour of Steven Fortune who invented it in 1986 and whose complexity is ${displaystyle O(nlog {n})}$ .

Calculation of the Voronoi diagram with the help of the straight sweep technique. It is noted that as the straight moves, the beach line changes by generating the Voronoi regions of the sites.

The Fortune algorithm is based on one of the key techniques within the computational geometry called a straight sweep. The essence of this technique lies in assuming that there is a straight line $ell$ that runs the plane from top to bottom (or from left to right, even in opposite directions) and that along its route is intersected with the structures we want to process. When this intersection is given, some information is stored in such a way that it helps in the calculations. It is necessary that the information obtained in regions already visited by the line be invariant. It is very common that it is technical to use two types of data structures: priority queue where they are saved events that are only points where the straight should stop and a binary search tree where the geometric elements that have been intersected with the straight are stored and it is necessary to remember for future processing. It should be noted that because the computer cannot emulate such as the continuous movement of the sweep line, it is necessary to devise a form of discretization of the movement of the line that is processable on the computer, hence the events are such discretization.

Combinatorial properties

To apply the straight sweep to the Voronoi diagram, intuitively, you could take to the set of sites ${displaystyle P={p_{1},dotsp_{n}}}$ like events and in this way carry the intersection of the sweeping line with the Voronoi diagram. However, because the calculation of ${displaystyle {mathcal {V}}(p_{i})}$ depends on the intersection $n - 1$ plans, then the invariant of the technique could not be maintained since even though $ell$ You have already processed a site, information regarding your Voronoi region will continue to change due to the remaining sites to be processed. Based on this, it is imperative to change the perspective and instead of maintaining the intersection of $ell$ with ${displaystyle Vor(P)}$ you need to keep information about those sites about $ell$ that can no longer change because of the sites below $ell$ .

Beach line for the Voronoi diagram.

It will denote the closed semi-plane over $ell$ Like ${displaystyle ell ^{+}}$ . What is the part of the Voronoi diagram on $ell$ that he will never be able to change, for which he has the following. Given a point ${displaystyle qin ell ^{+}}$ the distance from this at any point below $ell$ is bigger than the distance $q$ a $ell$ proper. In addition, the nearest site $q$ It can't be under $ell$ Yeah. $q$ is at least so close to somewhere. ${displaystyle p_{i}in ell ^{+}}$ Like $q$ He is. $ell$ . Therefore, the geometrical place of nearest points somewhere than to $ell$ is limited by a parable. Following this line, the geometrical place of all the points closest to somewhere on $ell$ to $ell$ in itself is embraced by a set of the most ${displaystyle 2n-1}$ Parabolic arches. This set of arches is called beach line. Every place ${displaystyle p_{i}}$ about the sweep line defines a parable completely. The beach line has the property of monotony since if you pass any vertical straight through it, it intersects it at exactly one point.

So, instead of keeping the intersection of ${displaystyle Vor(P)}$ with $ell$ , the beach line will be maintained as the sweep line moves. Obviously, the beach line cannot be explicitly represented as it is continuous and transforms each that $ell$ change position.

Generation of a new arch on the beach line.

A bow can appear on the beach line when $ell$ processes a new site, hence this takes the name site event. At this time a new parable (in vertical line shape because the right side is infinitely small) breaks over the beach line. As the beach line begins to descend, the newly created parable begins to become more extended. Moreover, as the parable grows, intersections are generated with other parables on the beach line, which begins to trace the edges of the Voronoi diagram.

A second sweeping line event arises when a bow $beta$ it becomes so small that it becomes a point. When this comes, the intersections I had $beta$ with the other arches ( ${displaystyle beta '}$ to the left and ${displaystyle beta ''}$ to the right) are joined. This encounter of the intersection points implies that two edges of the diagram are found. Consequently, a vertex has been formed $q$ of the Voronoi diagram. Graphically, $q$ is the center of a circle that passes through the sites ${displaystyle p',p}$ and ${displaystyle p''}$ for ${displaystyle beta ',beta }$ and ${displaystyle beta ''}$ respectively. When $ell$ reach the lowest point of this circle, holding a Circle event.

Data Structures and Algorithm

Fortune's algorithm requires three types of data structures:

Data structure to help save the portion of the diagram calculated so far. A double-connected list of DCEL edges is used for this. It will refer to it as ${displaystyle {mathcal {D}}}$ .
Priority link ${mathcal {Q}}$ to save the site and circle events that should process the sweeping line.
Balanced binary search tree ${mathcal {T}}$ keep the beach line. Since the beach line cannot be stored directly due to its continuous nature, the following is done. In the leaves ${mathcal {T}}$ , the arches of the beach line are kept, characterized by the site that defines them, keeping the order as the one that would be appreciated on the beach line really. On the other hand, the intermediate nodes represent the break points (where an arch breaks on the beach line) as tubals ${displaystyle p_{i}}$

The following pseudocode is based on that presented in the work of Mark de Berg et al.

Algoritmo ${displaystyle DiagramaVoronoi(P)}$

Entry. Set of sites ${displaystyle P={p_{1},dotsp_{n}}}$ on the plane.

Departure ${displaystyle Vor(P)}$ inside a restriction box in ${displaystyle {mathcal {D}}}$ .

Initialization

{mathcal {Q}}

with all sites; initialize

{mathcal {T}}

as a vacuum and a DCEL

{displaystyle {mathcal {D}}}

empty.

while

{mathcal {Q}}

It's not empty.

Remove the event with the coordinate

y

larger than

{mathcal {Q}}

if the event is a site event

{displaystyle p_{i}}

then

{displaystyle ManejarEventoSitio(p_{i})}

else

{displaystyle ManejarEventoCirculo(gamma)}

Where

gamma

represents the leaf

{mathcal {T}}

representing the arch that will disappear.

Computer restraining box containing all vertices

{displaystyle Vor(P)}

inside and a semi-arist to the box.

${displaystyle ManejarEventoSitio(p_{i})}$

Yeah.

{mathcal {T}}

is empty, insert

{displaystyle p_{i}}

. Otherwise do the following steps.

{mathcal {T}}

the bow

alpha

vertically over

{displaystyle p_{i}}

. If the leaf

alpha

He has a pointer toward

{mathcal {Q}}

, then it's a false alarm and must be removed from

{mathcal {Q}}

Replace the sheet

{mathcal {T}}

represented by

alpha

with a subtree with three leaves. The leaf in the center saves the site

{displaystyle p_{i}}

and two others keep

{displaystyle p_{j}}

that was originally in

alpha

. Save the loops

<math alttext="{displaystyle }" xmlns="http://www.w3.org/1998/Math/MathML">.pj,pi▪{displaystyle ≥p_{j},p_{i}<img alt="{displaystyle }" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2f137c43b1960f171fa0fa957b7f4eac2a747cee" style="vertical-align: -1.005ex; width:9.989ex; height:2.509ex;"/> and <math alttext="{displaystyle }" xmlns="http://www.w3.org/1998/Math/MathML">.pi,pj▪{displaystyle ≥p_{i},p_{j}<img alt="{displaystyle }" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c2b013352b5873897b738b5e38d35e86dd1fa5c4" style="vertical-align: -1.005ex; width:9.989ex; height:2.509ex;"/> representing the new breaking points.

Create new semi-arist records in

{displaystyle {mathcal {D}}}

for the edge that separates

{displaystyle {mathcal {V}}(p_{i})}

and

{displaystyle {mathcal {V}}(p_{j})}

which will be traced due to the breaking points.

Check the triplet of consecutive arches where the new arch

{displaystyle p_{i}}

is the left arch to see if the break points converge.

${displaystyle ManejarEventoCirculo(gamma)}$

Delete the sheet

gamma

which represents the arch to disappear

alpha

{mathcal {T}}

. Update tuplas that represent the breaking points. Reebalance

{mathcal {T}}

. Remove from

{mathcal {Q}}

all events involving

alpha

Add the center of the event's causing circle as a vertice record in

{displaystyle {mathcal {D}}}

. Create two semi-arists corresponding to the new breaking points of the beach line.

Check the new triplet of consecutive arcs he had to

alpha

in the middle if the two breaking points converge. If so, insert the corresponding event in

{mathcal {Q}}

. Do the same for triplet where

alpha

I was on the right.

Complexity

The algorithm runs on ${displaystyle O(nlog {n})}$ and use $O(n)$ storage. This is because of ${mathcal {T}}$ and ${mathcal {Q}}$ Take ${displaystyle O(log {n})}$ . DCEL operations take constant time. When an event is processed, a constant number of operations of such operations are executed. And since you have $O(n)$ events (due to theorem 2), then complexity is ${displaystyle O(nlog {n})}$ . For its part, the storage is linear again due to theorem 2.

Generalization to R. no {displaystyle mathbb {R} ^{n}}

Voronói Thesssation of a set of random points on the plane.

For every discrete topological set S of points in a Euclidean space and for almost every point x, there exists a point of S that is the closest to x. (Here, the term almost is used to indicate that there are exceptions in which x may be equidistant from two or more points of S.)

If S contains only two points, a and b, then the set of all points equidistant from both is a hyperplane of codimension 1. That hyperplane is the boundary between the points closer to a than to b, and the points closer to b than to a. In fact, that hyperplane is the bisector plane of the segment joining a and b. More generally, the set of points closer to a point c of S than to any other point of S (basin of attraction of c) is the interior of a convex (possibly unbounded) polytope called the Dirichlet domain or Voronoi cell of c >. The set of all these polytopes constitutes a complete tiling of Euclidean space, called the Voronói tiling associated with S.

If the dimension of the Euclidean space is only 2, as in the Euclidean plane, then it is very easy to draw Voronoi tilings, like the ones in the attached figure.

Applications

Process carried out in a Geographic Information System (GIS) to obtain axes of streets by using Thiessen polygons

Voronoi diagrams find applications in areas such as computer graphics, epidemiology, geophysics, and meteorology. One particularly notable use was in the analysis of the 1854 cholera epidemic in London by physician John Snow, who found a strong correlation of deaths with proximity to a certain—ultimately contaminated—water pump in Broad Street (in the Soho district). His well-known cholera map is today one of the classic examples of the use of the geographical method.

They have been used for the analysis of meteorological data (rain gauge stations), although currently they are also applied in studies in which service areas must be determined (hospitals, fire stations, subway stations, shopping centers, air traffic control, mobile telephony, population analysis of plant species, etc.). It is one of the basic analysis functions in Geographic Information Systems (GIS).

Contenido relacionado

Más resultados...