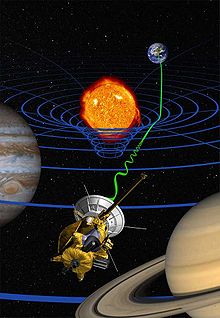
Theory of relativity
The theory of relativity includes both the theory of special relativity and the theory of general relativity, formulated mainly by Albert Einstein at the beginning of the 20th century, which sought to resolve the existing incompatibility between Newtonian mechanics and electromagnetism.
The theory of special relativity, published in 1905, deals with the physics of the movement of bodies in the absence of gravitational forces, in which Maxwell's equations of electromagnetism were made compatible with a reformulation of the laws of motion. In the theory of special relativity, Einstein, Lorentz and Minkowski, among others, unified the concepts of space and time, in a four-dimensional branch that was called space-time. Special relativity was a revolutionary theory for its time, with which Newton's absolute time was relegated and concepts such as the invariance in the speed of light, time dilation, length contraction and the equivalence between mass and energy they were introduced. Furthermore, with the formulations of special relativity, the laws of Physics are invariant in all inertial reference frames; As a mathematical consequence, the speed of light is found to be the upper limit and the deterministic causality that physics had until then is eliminated. It should be noted that Newton's laws of motion are a particular case of this theory where mass, when traveling at very low speeds, does not experience any variation in length or is transformed into energy and time can be considered absolute.
The theory of general relativity, published in 1915, is a theory of gravity that replaces Newtonian gravity, although it numerically coincides with it for weak gravitational fields and "small" velocities. The general theory reduces to the special theory in the presence of gravitational fields. General relativity studies the gravitational interaction as a deformation in the geometry of space-time. In this theory the concepts of the curvature of space-time are introduced as the cause of gravitational interaction, the equivalence principle that says that for all inertial local observers the laws of special relativity are invariant and the introduction of the movement of a particle by geodesic lines. General relativity is not the only theory that describes gravitational attraction, but it is the one that has found the most relevant verifiable data. Previously, the gravitational interaction was described mathematically by means of a mass distribution, but in this theory not only the mass perceives this interaction, but also the energy, through the curvature of space-time and for this reason another mathematical language is needed. to be able to describe it, the tensor calculus. Many phenomena, such as the bending of light by gravity and the deflection in Mercury's orbit, are perfectly predicted by this formulation. General relativity also opened up another field of research in physics, known as cosmology and is widely used in astrophysics.
On March 7, 2010, the Israel Academy of Sciences put on public display Einstein's original manuscripts (written in 1905). The document, which contains 46 pages of handwritten text and mathematical formulas, was donated by Einstein to the Hebrew University of Jerusalem in 1925 on the occasion of its inauguration.
Main concepts
The basic assumption of the theory of relativity is that the location of physical events, both in time and space, are relative to the state of motion of the observer: thus, the length of a moving object or the The instant in which something happens, unlike what happens in Newtonian mechanics, are not absolute invariants, and different observers moving relative to each other will differ with respect to them (lengths and time intervals, in relativity are relative and not absolute).
Special Relativity
The theory of special relativity, also called the theory of special relativity, was published by Albert Einstein in 1905 and describes the physics of motion in the framework of flat space-time. This theory correctly describes the movement of bodies even at high speeds and their electromagnetic interactions, it is basically used to study inertial reference systems (it is not applicable for astrophysical problems where the gravitational field plays an important role).
These concepts were previously introduced by Poincaré and Lorentz, who are considered precursors of the theory. Although the theory solved a good number of problems in electromagnetism and gave an explanation of the Michelson and Morley experiment, it does not provide an adequate relativistic description of the gravitational field.
After the publication of Einstein's article, the new theory of special relativity was accepted in a few years by practically all physicists and mathematicians. In fact, Poincaré or Lorentz had been very close to reaching the same result as Einstein. The definitive geometric form of theory is due to Hermann Minkowski, a former professor of Einstein at the Zurich Polytechnic; he coined the term "space-time" (“space-time”).Raumzeit) and gave it the proper mathematical form. Minkowski's time-space is a tetradimensional variety in which the three spatial dimensions and time were intertwined in an indissoluble way. In this time-space of Minkowski, the motion of a particle is represented by its line of universe (Weltlinie), a curve whose points are determined by four different variables: the three spatial dimensions (x{displaystyle x },and{displaystyle and},z{displaystyle z }) and time (t{displaystyle t }). The new Minkowski scheme forced to reinterpret the existing metric concepts until then. The three-dimensional concept of point was replaced by the Success. The magnitude of distance replaced by the magnitude of interval.
General Relativity

The general theory of relativity or general relativity is a theory of gravitational field and general reference systems, published by Albert Einstein in 1915 and 1916.
The name of the theory is because it generalizes the so-called special theory of relativity and the principle of relativity for an arbitrary observer. The fundamental principles introduced in this generalization are the principle of equivalence, which describes acceleration and gravity as aspects other than the same reality, the notion of the curvature of space-time and the principle of generalized covariance. The theory of general relativity proposes that the very geometry of space-time is affected by the presence of matter, which results in a relativistic theory of the gravitational field. In fact the theory of general relativity predicts that space-time will not be flat in the presence of matter and that the curvature of space-time will be perceived as a gravitational field.
Einstein's basic intuition was postulate that at a specific point it cannot be experimentally distinguished between a uniformly accelerated body and a uniform gravitational field. The general theory of relativity also allowed the reformulation of the field of cosmology.
Einstein expressed the purpose of the theory of general relativity to fully implement the Ernst Mach program of relativization of all the effects of inertia, even adding the so-called constant cosmological to their field equations for this purpose. This real point of contact of the influence of Ernst Mach was clearly identified in 1918, when Einstein distinguishes what he baptized as the principle of Mach (the inertial effects are derived from the interaction of the bodies) of the principle of general relativity, which is now interpreted as the principle of general covariance.
German mathematician David Hilbert wrote and made public the equations of covariance before Einstein, it resulted in not a few accusations of plagiarism against Einstein, but probably more because it is a geometric (or perspective) theory. The same postulates that the presence of mass or energy "curves" space-time, and this curvature affects the trajectory of mobile bodies and even the trajectory of light.Formalism of the theory of relativity
Particles
In the theory of relativity a punctual particle is represented by a pair (γ γ (Δ Δ ),m){displaystyle (gamma (tau),m);}Where γ γ (Δ Δ ){displaystyle gamma (tau);} is a differential curve, called the universe line of the particle, and m is a climbing that represents the mass at rest. The tangent vector to this curve is a temporary vector called quadrilocity, the product of this vector by the resting mass of the particle is precisely the quadruplement. This quadruple is a four-component vector, three of these components are called space and represent the analogous relativist of the linear moment of classical mechanics, the other component called the temporary component represents the relativistic generalization of kinetic energy. In addition, given an arbitrary curve in space-time, the so-called intervalwhich is obtained from the metric tensor. The relativistic interval measured throughout the trajectory of a particle is proportional to the time interval of its own or time interval perceived by the particle.
Fields
When considering fields or continuous mass distributions, some kind of generalization is needed for the notion of a particle. A physical field has momentum and energy distributed in space-time, the concept of quadri-momentum is generalized through the so-called energy-momentum tensor that represents the distribution in space-time of both energy and linear momentum. In turn, a field, depending on its nature, can be represented by a scalar, a vector or a tensor. For example the electromagnetic field is represented by a fully antisymmetric second order tensor or 2-form. If the variation of a field or a distribution of matter is known, in space and time, then there are procedures to construct its energy-momentum tensor.
Physical magnitudes
In relativity, these physical magnitudes are represented by 4-dimensional vectors or by mathematical objects called tensors, which generalize vectors, defined over a four-dimensional space. Mathematically these 4-vectors and 4-tensors are defined elements of the vector space tangent to space-time (and the tensors are defined and built from the tangent or cotangent bundle of the manifold that represents space-time).
| Euclid three-dimensional space | Space-time of Minkowski |
|---|---|
| Period | Success |
| Length | Intervalo |
| Speed | Cuadrivelocity |
| Momentum | Cuadrimomentum |
In addition to quadrivectors, quadritensors are also defined (ordinary tensors defined on the tangent bundle of space-time conceived as a Lorentzian variety). The curvature of space-time is represented by a 4-tensor (fourth-order tensor), while the energy and momentum of a continuum or the electromagnetic field are represented by 2-tensors (symmetrical the energy-momentum tensor, antisymmetric the electromagnetic field). Fourvectors are in fact 1-tensors, in this terminology. In this context it is said that a magnitude is a relativistic invariant if it has the same value for all observers, obviously all relativistic invariants are scalars (0-tensors), frequently formed by the contraction of tensor magnitudes.
The relativistic interval
The relativistic interval can be defined in any space-time, either this plane as in the special relativity, or curved as in general relativity. However, for simplicity, we will initially discuss the concept of interval for a flat space-time. The metric tensor of Minkowski's flat space-time is designated with the letter MIL MIL ij{displaystyle scriptstyle eta _{ij}and in Galilean or inertial coordinates takes the following form:
gij=MIL MIL ij=(c20000− − 10000− − 10000− − 1){displaystyle g_{ij}=eta _{ij}={begin{pmatrixc^{2}{2}{1}{0}{0}{}{}{}{}{}{}{}{}{}{}{}{}={begin}={begin{begin}={begin{begin{begin{b}={b}{b}{b}{b}{b}{x{b}{f}}{f}{f}{f}{f}{f}={f}={f}{f}{f}{f}}{f}{f}{f}={f}={f}={f}{fm}={f}{f}={f}={f}{f}
The interval, the dimensional distance, is represented by expression ds2{displaystyle ds^{2} }calculated as follows:
- ds2=gijdxidxj{displaystyle ds^{2} =g_{ij}dx^{i}dx^{j}}
- ds2=c2(dx0)2− − (dx1)2− − (dx2)2− − (dx3)2{displaystyle ds^{2} =c^{2}(dx^{0})^{2-}(dx^{1})^{2}-(dx^{2})^{2}-(dx^{3})^{2}}
- ds2=c2dt2− − dx2− − dand2− − dz2=c2dt2− − (dx2+dand2+dz2){displaystyle ds^{2} =c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}=c^{2}dt^{2}-dx^{2}-(dx^{2}+dy^{2}+dz^{2})}}
- ds2=c2dt2− − dl2{displaystyle ds^{2} =c^{2}dt^{2}-dl^{2}}}
Intervals can be classified into three categories: Intervals space (when) ds2{displaystyle ds^{2}} is negative), temporary (SIGHS) ds2{displaystyle ds^{2}} is positive) and null (when) ds2=0{displaystyle scriptstyle ds^{2}=0}). As the reader may have checked, the null intervals are those that correspond to particles that move at the speed of light, such as photons: The distance dl2{displaystyle dl^{2}} traveled by the photon is equal to its speed (c) multiplied by time dt{displaystyle scriptstyle dt} and therefore the interval ds2=c2dt2− − dl2{displaystyle scriptstyle ds^{2}=c^{2}dt^{2}-dl^{2}}} It gets null.
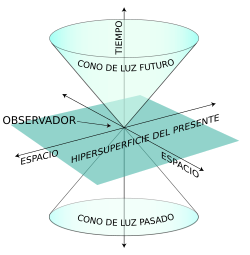
Null intervals can be represented in the form of a light cone, popularized by Stephen Hawking's famous book, A Brief History of Time. Whether an observer is located at the origin, the absolute future (the events that will be perceived by the individual) is displayed at the top of the ordinate axis, the absolute past (events that have already been perceived by the individual) at the bottom, and the present perceived by the observer at point 0. Events that are outside the light cone do not affect us, and are therefore said to be They are located in areas of space-time that have no causal relationship with ours.
Imagine, for a moment, that in the Andromeda galaxy, located 2.5 million light years from us, a cosmic cataclysm occurred 100 000 years ago. Since, first: Andromeda's light takes 2 million years to get to us and second: nothing can travel at a speed superior to that of the photons, it is evident that we have no way to know what happened in that Galaxy only 100,000 years ago. It is therefore said that the interval between such hypothetical cosmic catastrophe and we, observers of the present, is a Space interval (<math alttext="{displaystyle ds^{2}ds2.0{displaystyle ds^{2}{2} implied}<img alt="ds^{2}), and therefore, it cannot affect the individuals who currently live on Earth: that is, there is no causal relationship between that event and us.

- Analysis
The only problem with this hypothesis is that when entering a black hole, spacetime is annulled, and as we already know, something that contains some volume or mass must have at least a space where it can be located, the time in In this case, it is not important, but space plays a very important role in the location of volumes, so this is very unlikely, but not impossible for the technology.
We can choose another even more illustrative historical episode: That of the star of Bethlehem, as it was interpreted by Johannes Kepler. This German astronomer considered that said star was identified with a supernova that took place in the year 5 BC. C., whose light was observed by contemporary Chinese astronomers, and which was preceded in previous years by several planetary conjunctions in the constellation of Pisces. That supernova probably went off thousands of years ago, but its light didn't reach Earth until 5 B.C. C. Hence, the interval between said event and the observations of Egyptian and megalithic astronomers (which took place several centuries before Christ) is a spatial interval, since the radiation of the supernova could never get to them On the contrary, the supernova explosion on the one hand, and the observations made by the three wise men in Babylon and by Chinese astronomers in 5 B.C. C. on the other, they are linked together by a temporary interval, since the light was able to reach said observers.
Time and interval are related by the following equivalence: cdΔ Δ =ds{displaystyle scriptstyle cdtau =ds}, that is, the interval is equal to the local time multiplied by the speed of light. One of the characteristics of both the local time and the interval is its invariance against the coordinate transformations. Whatever our point of reference, whatever our speed, the interval between a given event and we remain invariant.
This invariance is expressed through the call hyperbolic geometry: The interval equation ds{displaystyle scriptstyle ds} has the structure of a hyperbola over four dimensions, whose independent term match the value of the square of the interval (ds2=dt2− − dl2{displaystyle scriptstyle ds^{2}=dt^{2}-dl^{2}), as just said in the previous paragraph, is constant. The Soon of the hyperbola would come to coincide with the cone of light.
Quadrivelocity, acceleration and quadrimomentum
In Minkowski space-time, the kinematic properties of particles are fundamentally represented by three magnitudes: Quadrivelocity (or tetravelocity), quadriaceleration, and quadrimomentum (or tetramomentum).
The quadrantness is a tangent quadrant to the universe line of the particle, related to the coordinated speed of a measured body by an observer at any rest, this Coordinated speed is defined with the Newtonian expression dxi/dt{displaystyle dx^{i}/dt}Where (t,x1,x2,x3){displaystyle (t,x^{1},x^{2},x^{3});} are the time coordinated and the spatial coordinates measured by the observer, for which the expanded Newtonian speed would be given by (1,v1,v2,v3){displaystyle (1,v^{1},v^{2},v^{3}),}. However, this Newtonian measure of velocity is not useful in relativity theory, because the Newtonian speeds measured by different observers are not easily commensurate because they are not covariant magnitudes. Thus in relativity a modification is introduced in the expressions that give notice of speed, introducing a relativistic invariant. This invariant is precisely the time proper to the particle that is easily related to the coordinated time of different observers. Using the relationship between own time and coordinated time: dt=γ γ dΔ Δ {displaystyle dt=gamma dtau ;} defined the quadrilocity [proper] multiplying γ γ {displaystyle gamma } the coordinated speed: uα α =vα α γ γ =dxi/dΔ Δ {displaystyle u^{alpha }=v^{alpha }gamma =dx^{i}/dtau }.
The coordinated velocity of a body with mass depends capriciously on the reference system that we choose, while the quadrantlocity itself is a magnitude that is transformed according to the principle of covariance and has an ever constant value equivalent to the interval divided between the time itself (ds/dΔ Δ {displaystyle ds/dtau }), or what is the same, at the speed of light c. For particles without mass, such as photons, the previous procedure cannot be applied, and quadrantlocity can be defined simply as a tangent vector to the trajectory followed by them.
La quadruple can be defined as the temporary derivative of quadrantility (ai=dui/dΔ Δ {displaystyle a^{i}=du^{i}/dtau }). Its magnitude is equal to zero in the inertial systems, whose lines of the world are geodesic, straight in the plain space-time of Minkowski. On the contrary, the curved world lines correspond to particles with a different acceleration of zero, to non-inertial systems.
Along with the principles of invariance of the interval and quadrantility, the fundamental role of the conservation law of the quadimomentum. The Newtonian definition of momentum is applicable here (p→ → =μ μ u→ → {displaystyle {vec {p}}=mu {vec {u}}}}) as the mass (in this case preserved, μ μ {displaystyle mu }) multiplied by speed (in this case, quadrantility), and therefore its components are the following: (m,p1,p2,p3){displaystyle (m,p^{1},p^{2},p^{3});}taking into account that m=μ μ γ γ {displaystyle m=mu gamma ;}. The amount of maintained is defined as the square root of the norm of the vector of quadimomentum. The maintained momentum, as well as the interval and quadrantility itself, remains invariant with the transformations of coordinates, although there is also a distinction between bodies with mass and the photons. In the first, the magnitude of the quadiomentum is equal to the mass multiplied by the speed of light (日本語p日本語=μ μ c{displaystyle 日本語p). On the contrary, the preserved quadimomentum of the photons equals the magnitude of its three-dimensional momentum (日本語p日本語=p{displaystyle 日本語p).
As both the speed of the light and the quadimomentum are preserved quantities, so is its product, to which the name is given Conserved energy (Ecorn=日本語p日本語c{displaystyle E_{con}=) that in the bodies with mass equals the mass multiplied by the speed of light to square (Ecorn=μ μ c2{displaystyle E_{con}=mu c^{2}}, the famous Einstein formula) and the photons to the momentum multiplied by the speed of light (Ecorn=pc{displaystyle E_{con}=pc})
Components → → (p0,p1,p2,p3)→ → (μ μ γ γ ,μ μ v1γ γ ,μ μ v2γ γ ,μ μ v3γ γ )→ → (m,p1,p2,p3){displaystyle to (p^{0},p^{1},p^{2},p^{3})to (mu gammamu v^{1}gammamu v^{2}gammamu v^{3}gammato (m,p^{1},p^{2},p^{3}}}}}
Magnitude of the quadimomentum → → 日本語p日本語=p→ → ⋅ ⋅ p→ → =m2c2− − p2=E2c2− − p2{displaystyle to Șp={sqrt {{vec {p}}}{cdot {vec {p}}}}}}{sqrt {m^{2}c^{2}-p^{2}}}}}}{{{sqrt {{frac}}}{c^{c^{2}}}}}{c}}}}}}}}{{{c {{s}}}}}}}}}}}}}}}{{{
Magnitude in bodies with mass → → 日本語p日本語=p→ → ⋅ ⋅ p→ → =mu→ → ⋅ ⋅ u→ → =μ μ c{displaystyle to Șp={sqrt {{vec {p}}}{cdot {vec {p}}}}}}=m{sqrt {{vec {u}}}{cdot {vec {u}}}}}}}{mu c}
Magnitude in photons (mass = 0) → → 日本語p日本語=p→ → ⋅ ⋅ p→ → =m2c2− − p2=p2=p{displaystyle to Șp={sqrt {{vec {p}}}{cdot {vec {p}}}}}}}={sqrt {m^{2}c^{2}-p^{2}}}}}{{{sqrt {p^{2}}}}
Energy → → Ecorn=c日本語p日本語=cp→ → ⋅ ⋅ p→ → =E2− − p2c2{displaystyle to E_{con}=ccultp info=c{sqrt {{{vec {p}}}}cdot {vec {p}}}}}}}{sqrt {E^{2}-p^{2}c^{2}}}}}}}}
Energy in bodies with mass (resting bodies, p=0) → → Ecorn=m2c4− − p2c2→ → Ecorn=mc2{displaystyle to E_{con}={sqrt {m^{2}c^{4-p^{2}c^{2}}}}}to E_{con}=mc^{2}}}}
Energy in photons (mass at rest = 0) → → Ecorn=m2c4− − p2c2=p2c2=pc{displaystyle to E_{con}={sqrt {m^{2}c^{4-p^{2}c^{2}}}}{sqrt {p^{2}c^{2}}}}}}=pc}
The apparition of Special Relativity put an end to the secular dispute that kept within the classical mechanics the schools of the Mechanists and energetistas. The first held, following Descartes and Huygens, that the magnitude preserved in every movement was constituted by the momentum the total of the system, while the energetists - which took the Leibniz studies on the basis - considered that the preserved magnitude was made up of the sum of two quantities: living force, equivalent to half the mass multiplied by speed to square (mv2/2{displaystyle mv^{2}/2}to which today we would call "kinetic energy", and the Dead forceequivalent to height by constant g (hg{displaystyle hg}), which would correspond to “potential energy”. It was the German physicist Hermann von Helmholtz who first gave to the Lebnizian forces the generic denomination of energy and the one that formulated Energy Conservation Actwhich is not restricted to mechanics, which also extends to other physical disciplines such as thermodynamics.
Newtonian mechanics confirmed both postulates, stating that both momentum and energy are conserved magnitudes in all motion subjected to conservative forces. However, Special Relativity went one step further, since from the work of Einstein and Minkowski momentum and energy were no longer considered as independent entities and were considered as two aspects, two facets of one the only conserved quantity: the quadrimomentum.
| Concept | Components | Algebraic expression | Particles with mass | Photo |
|---|---|---|---|---|
| Intervalo | dxa=[chuckles]dtdx1dx2dx3]{displaystyle dx^{a}={begin{bmatrix}dtdx^{1}dx^{2}dx^{3}{3}end{bmatrix}}}}}}} | ds2=d→ → x⋅ ⋅ d→ → x{displaystyle ds^{2}={vec {d}}xcdot {vec {d}}x | ds2I was.0{displaystyle ds^{2}not =0} | ds2=0{displaystyle ds^{2}=0} |
| Cuadrivelocity | uα α =dxα α dΔ Δ =[chuckles]γ γ v1γ γ v2γ γ v3γ γ ]{displaystyle u^{alpha }={frac {dx^{alpha}{dtau }={begin{bmatrix}gamma \v^{1}gamma \v^{2}{2}gamma \v^{3}gamma \gamma \\end{bmatrix}}}}}}}}}}}}}}}}}{gamma | 日本語u日本語=u→ → ⋅ ⋅ u→ → =ds2dΔ Δ 2{displaystyle Δuint={sqrt {{vec {u}}}{cdot {vec {u}}}}={sqrt {frac {{ds^{2}}}{dtau ^{2}}}}}}}}}} | 日本語u日本語=c{displaystyle | Cuadrivelocity not defined |
| Acceleration | aα α =d2xα α dΔ Δ 2{displaystyle a^{alpha }={frac {d^{2}x^{alpha }}{dtau ^{2}}}}} | {displaystyle} | aα α =0{displaystyle a^{alpha }=0} (inertial systems) aα α I was.0{displaystyle a^{alpha }not =0} (non-inerial systems) | Acceleration not defined |
| Cuadrimomentum | pα α =μ μ uα α =[chuckles]m− − p1− − p2− − p3]{displaystyle p^{alpha }=mu u^{alpha }={begin{bmatrix}m-p^{1}-p^{2}-p^{3}\end{bmatrix}}}}}}} | 日本語p日本語=p→ → ⋅ ⋅ p→ → =E2c2− − p2{displaystyle Δp1}={sqrt {{vec {p}}}{cdot {vec {p}}}}={sqrt {{frac {E^{2}}}{c⁄2}}}}}}}{cdot {c}{c {cd}}}}}}}}}{cd}}}}{cd}}}}}}}{c {c {cd}{cd}}}{c {c {cd {cd {cd {cd {c {cd {c {cd {cd {cd {cd {cd {cd {cd {cd {cd {cd {cd {cd {cd}}}}{cd {cd {cd {cd}}}}}}}{cd}}}}}}{ | 日本語p日本語=μ μ c{displaystyle Δp1⁄4} | 日本語p日本語=p{displaystyle أعربية} |
The energy-momentum tensor (Tab)
Three are the fundamental equations that in Newtonian physics describe the phenomenon of universal gravitation: the first, affirms that the gravitational force between two bodies is proportional to the product of its masses and inversely proportional to the square of its distance (1); the second, that the gravitational potential (≈ ≈ {displaystyle Phi }) at a certain point is equal to the mass multiplied by the constant G and divided by distance r (2); and the third, finally, is the so-called Poisson equation (3), which indicates that the laplatian of gravitational potential is equal to 4π π Gρ ρ {displaystyle 4pi Grho }Where ρ ρ {displaystyle rho } is mass density in a given spherical region.
F=GMmr2(1){displaystyle F={frac {GMm}{r^{2}}}}(1)}→ → ≈ ≈ =GMr(2){displaystyle to Phi ={frac {GM}{r}}(2)}→ → Δ Δ ≈ ≈ =4π π Gρ ρ (3){displaystyle to Delta Phi =4pi Grho (3)}
However, these equations are not compatible with Special Relativity for two reasons:
- First mass is not an absolute magnitude, but its measurement derives from different results depending on the relative speed of the observer. Hence mass density ρ ρ {displaystyle rho } cannot serve as a gravitational interaction parameter between two bodies.
- Secondly, if the concept of space is relative, it is also the notion of density. Clearly, the contraction of space produced by the increase in the speed of an observer, prevents the existence of densities that remain unchanged in the face of Lorentz's transformations.
Therefore, it is necessary to dispense with the term ρ ρ {displaystyle rho }, located on the right side of the Poisson formula and replace it with a geometric-mechanical object that remains invariant to the transformations of Lorentz: This object was defined by Einstein in his universe equations and receives the name of energy-momentum tensor (Tα α β β {displaystyle T^{alpha beta}}). Its coefficients describe the amount of tetramomentum pα α {displaystyle p^{alpha}} that goes through a hypersurface Русский Русский β β {displaystyle pi _{beta }normal to the unit vector u→ → β β {displaystyle {vec {u}}{beta }}. Thus, the momentum tensor can be expressed through the following equation:
pα α =∫ ∫ Русский Русский Tα α β β dРусский Русский β β {displaystyle p^{alpha }=int _{Pi }T^{alpha beta }dPi _{beta }}
Or what is the same: The component pα α {displaystyle p^{alpha}} of tetramomentum is equal to the integral of hypersurface dРусский Русский β β {displaystyle dPi _{beta }} of tension-energy tensor. In an ideal fluid, from which both viscosity and heat driving are absent, tetramomentum components are calculated as follows:
Tα α β β =(ρ ρ +Pc2)uα α uβ β − − Pgα α β β {displaystyle T^{alpha beta },=left(rho +{P over c^{2}right)u^{alpha }u^{beta }-Pg^{alpha beta }}}}
where ρ ρ {displaystyle rho } It's the mass-energy density (mass per three-dimensional volume unit), P{displaystyle P} It's the hydrostatic pressure, uα α {displaystyle u^{alpha}} It's the fluid quadrantilityand gα α β β {displaystyle g^{alpha beta }} It's the reverse matrix of the metric tensor of the variety.
Furthermore, if the components of the tensor are measured by an observer at rest relative to the fluid, then the metric tensor is simply the Minkowski metric:
- gα α β β =MIL MIL α α β β =diag (c2,− − 1,− − 1,− − 1){displaystyle g_{alpha beta },=eta _{alpha beta }=operatorname {diag} (c^{2},-1,-1,-1)}}}}}
- gα α β β =MIL MIL α α β β =diag (1c2,− − 1,− − 1,− − 1){displaystyle g^{alpha beta },=eta ^{alpha beta }=operatorname {diag} left({frac {1}{c^{2}}}}},-1,-1right)}}
Since, in addition, the tetravelocity of the fluid with respect to the observer at rest is:
- uα α =(1,0,0,0){displaystyle u^{alpha }=(1,0,0,0)}
as a consequence of this, the coefficients of the stress-energy tensor are the following:
Tα α β β =(ρ ρ 0000− − P10000− − P20000− − P3){displaystyle T^{alpha beta }={begin{pmatrix}rho &0 fake0 fake-P_{1}{1}{0 fake0\0 fake-P_{2}{2}{0 fake0}{0}{0}{3}end{pmatrix}}}}}}
Where ρ ρ {displaystyle rho } It's the mass densityand Pi{displaystyle P_{i}} are the three-dimensional components of the hydrostatic pressure. As we see, the gravitational field has two different sources: the mass and momentum of the fluid in question. The gravitational effects originated by the mass are called gravitoelectric effects, while those due to momentum receive the name of gravitomagnetic effects. The first have a intensity c2{displaystyle c^{2}} superior to the seconds, which only manifest in those cases in which fluid particles move with a speed close to that of light (it is then spoken of relativistic fluids): This is the case of jets (jets) that emanate from the center of the galaxy and which are propelled in the two directions marked by the rotation axis of this cosmic body; of the matter that is precipitated into a black hole; and of the stellar fluid that is directed towards the center of the star when it enters into collapse. In the latter case, during the final phases of the star's contraction process, hydrostatic pressure can become as strong as to accelerate the collapse rather than slow it down.
We can, from the voltage-energy tensor, calculate how much mass contains a certain volume of the fluid: By removing the definition of this tensor exposed a few lines above, you can define the coefficient T00{displaystyle T^{00} like the amount of momentum p0{displaystyle p^{0}} (this is it, the mass) that goes through the hypersurface dРусский Русский 0{displaystyle dPi _{0}}. In Minkowski's space-time, hyper-surface dРусский Русский 0{displaystyle dPi _{0}} is that region that is defined by the three normal vector bases to the vector dx0{displaystyle dx^{0}}: Русский Русский 0{displaystyle pi _{0}} is therefore a three-dimensional volume, defined by the base vectors e→ → 1{displaystyle {vec {e}}_{1}} (laughs) x), e→ → 2{displaystyle {vec {e}}_{2}}} (laughs) and), and e→ → 3{displaystyle {vec {e}}_{3}} (laughs) z). We can therefore write:
- p0=∫ ∫ T00dРусский Русский 0{displaystyle p^{0}=int T^{00}dPi _{0}}
- m=∫ ∫ ρ ρ dV{displaystyle m=int rho dV}
In the same way, it is possible to mathematically deduce from the stress-energy tensor the Newtonian definition of pressure, introducing into the aforementioned equation any pair of indices that are different from zero:
- p1=∫ ∫ Русский Русский T11dРусский Русский 1{displaystyle p^{1}=int _{Pi }T^{11}dPi _{1}
Hypersurface dРусский Русский 1{displaystyle dPi _{1}} is that space-time region defined by the three normal unit vectors to dx1{displaystyle dx_{1}} (this is the two space vectors, e→ → 2{displaystyle {vec {e}}_{2}}} and e→ → 3{displaystyle {vec {e}}_{3}}, corresponding to the axles and and zand the temporary vector e→ → 0{displaystyle {vec {e}}_{0}} - dt{displaystyle dt}as you prefer. This definition allows us to break down the entire hypersurface into a temporary integral (whose integration is defined by dt{displaystyle dt}and another surface (this time two-dimensional, dS{displaystyle dS}(c):
- p1=∫ ∫ ∫ ∫ S− − P1dS1dt{displaystyle p^{1}=int int _{S}-P_{1}dS_{1}dt}
Finally, we partially derive both sides of the equation with respect to time, and taking into account that the force is nothing more than the rate of temporary increase of the momentum, we obtain the following result:
- F1=∫ ∫ − − P1dS1{displaystyle F^{1}=int-P_{1}dS_{1}}
Containing the Newtonian definition of pressure as a force exerted per unit area.
The Electromagnetic Tensor (Fab)
The equations deduced by the Scottish physicist James Clerk Maxwell showed that electricity and magnetism are nothing more than two manifestations of the same physical phenomenon: the electromagnetic field. Now, to describe the properties of this field, physicists at the end of the XIX century had to use two different vectors, the corresponding ones electric and magnetic fields.
It was the advent of special relativity that made it possible to describe the properties of electromagnetism with a single geometric object, the quadipotential vector, whose temporal component corresponded to the electric potential, while its spatial components they were the same as those of the magnetic potential.
- Aα α =(V,Ax,Aand,Aand){displaystyle A^{alpha }=(V,A_{x},A_{y},A_{y}}}}}}
In this way, the electric field can be understood as the sum of the gradient of the electric potential plus the time derivative of the magnetic potential:
- E=− − ► ► V− − ▪ ▪ A▪ ▪ t{displaystyle E=-nabla V-{frac {partial A}{partial t}}}}
and the magnetic field, as the curl of the magnetic potential:
- B=► ► × × A{displaystyle B=nabla times A}
The properties of the electromagnetic field can also be expressed using a second-order tensor called Faraday tensor and obtained by externally differentiating the quadripotential vector Aα α {displaystyle A^{alpha}}
- Fα α β β =▪ ▪ α α Aβ β − − ▪ ▪ β β Aα α {displaystyle F_{alpha beta }=partial _{alpha }A_{beta}-partial _{beta }A_{alpha }}}}}}
Fα α β β =(0Ex/cEand/cEz/c− − Ex/c0Bz− − Band− − Eand/c− − Bz0Bx− − Ez/cBand− − Bx0);Fβ β α α =(0ExEandEz− − Ex0Bz− − Band− − Eand− − Bz0Bx− − EzBand− − Bx0)♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪ ♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪
The Lorentz force can be deduced from the following expression:
- fα α =qFβ β α α uβ β {displaystyle f^{alpha }=qF_{beta }^{alpha }u^{beta }}}
- F=q(E+u× × v){displaystyle F=q(E+utimes v)}
Where q It's the load. uα α {displaystyle u^{alpha }} the quadrantness of the particle.
Contenido relacionado
Heinrich Rudolph Hertz
Atomic nucleus
Higgs' Boson