Theorem
A theorem is a proposition whose truth is proved. In mathematics, it is any proposition that, based on an assumption (hypothesis), affirms a reasonableness (thesis) that is not self-evident.
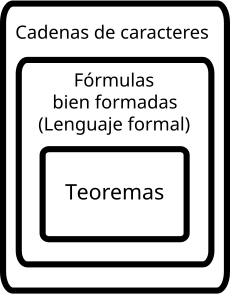
It can also be said that a theorem is a well-formed formula that can be proved within a formal system, starting from axioms, notions and other theorems. Proving theorems is a central issue in mathematical logic. Theorems can also be expressed in formalized natural language.
Theorems generally have a number of premises that must be listed or clarified beforehand. The conclusion of the theorem is a logical or mathematical statement that is true under the given conditions. The informative content of the theorem is the relationship between the hypotheses and the thesis or conclusion.
A corollary is called a logical statement that is the immediate consequence of a theorem, and can be proved using the properties of the reference theorem.
Theorem
A theorem requires a logical framework; This framework will consist of a set of axioms (axiomatic system) and an inference process, which allows theorems to be derived from the axioms and theorems that have been derived but are not axioms.
In propositional and first-order logic, any proven statement is called a theorem. More specifically in logic, a finite sequence of well-formed formulas (well-formed logical formulas) is called a demonstration F1,...,Fn , such that each Fi is either an axiom or a theorem that follows from two previous formulas Fj and Fk (such that j<i and k<i) by means of a deduction rule. Given a proof like the one above, if the final element Fn is not an axiom then it is a theorem. Summarizing the above, it can be said formally, a theorem is a well-formed formula, which is not an axiom, and which can be the final element of some proof, that is, a theorem is a well-formed formula for for which there is a proof.
Theorem and truth
Until the end of the 19th century and the founding crisis of mathematics, all mathematical theories were built from a few basic properties that were considered self-evident; for example, the facts that every natural number has a successor, and that there is exactly one line through two given distinct points. These basic properties that were considered absolutely self-evident were called postulates or axioms; For example, Euclid's postulates. All theorems were proved using these basic properties implicitly or explicitly, and because of the evidence of these basic properties, a proven theorem was considered to be definitely true, unless there was an error in the proof. For example, the sum of the interior angles of a triangle is equal to 180°, and this was considered an undoubted fact.
One aspect of the founding crisis of mathematics was the discovery of non-Euclidean geometries that do not lead to any contradiction, even though, in such geometries, the sum of the angles of a triangle is different from 180°. So, the property "the sum of the angles of a triangle is equal to 180°" is true or false, depending on whether Euclid's fifth postulate is assumed or denied. Similarly, the use of basic "obvious" of sets leads to the contradiction of Russell's paradox. This has been solved by elaborating the rules that are allowed to manipulate sets.
This crisis has been resolved by revising the foundations of mathematics to make them more rigorous. On these new foundations, a theorem is a well-formed formula of a mathematical theory that can be proved from the theory's axioms and rules of inference. Then, the previous theorem about the sum of the angles of a triangle becomes: Under the axioms and rules of inference of Euclidean geometry, the sum of the interior angles of a triangle is equal to 180°. Similarly, Russell's paradox disappears because, in an axiomatized set theory, the "set of all sets" it cannot be expressed with a well-formed formula. More precisely, if the set of all sets can be expressed with a well-formed formula, this implies that the theory is inconsistent, and every well-formed statement, as well as its negation, is a theorem.
In this context, the validity of a theorem depends solely on the correctness of its proof. It is independent of the truth, or even the meaning of the axioms. This does not mean that the meaning of the axioms is not interesting, but rather that the validity of a theorem is independent of the meaning of the axioms. This independence can be useful by allowing results from some area of mathematics to be used in apparently unrelated areas.
An important consequence of this way of thinking about mathematics is that it allows one to define mathematical theories and theorems as mathematical objects, and to prove theorems about them. Examples are Gödel's incompleteness theorems. In particular, there are well-formed statements that can be shown not to be a theorem of environmental theory, although they can be shown in a broader theory. An example is Goodstein's theorem, which can be stated in Peano arithmetic, but is shown to be unprovable in Peano arithmetic. However, it is provable in some more general theories, such as the Zermelo-Fraenkel set theory.
Epistemological considerations
Many mathematical theorems are conditional statements, the proofs of which draw conclusions from conditions known as hypotheses or premises. In light of the interpretation of evidence as a justification of the truth, the conclusion is often seen as a necessary consequence of the hypotheses. That is to say, that the conclusion is true in case the hypotheses are true, without further assumptions. However, the conditional could also be interpreted differently in certain deductive systems, depending on the meanings assigned to the derivation rules and the conditional symbol (for example, non-classical logic).
Although theorems can be written in a completely symbolic form (for example, as propositions in propositional calculus), they are often expressed informally in a natural language such as English for better readability. The same is true of proofs, which are often expressed as logically organized and clearly worded informal arguments, intended to convince readers of the truth of the theorem statement beyond doubt, and from which one can, in principle, build a formal symbolic demonstration.
In addition to better readability, informal arguments are often easier to verify than purely symbolic ones; in fact, many mathematicians would express a preference for a proof that not only proves the validity of a theorem, but also explains in some way "why" is obviously true. In some cases, one could even prove a theorem using an image as proof.
Because theorems lie at the core of mathematics, they are also fundamental to its aesthetics. Theorems are often described as "trivial", "difficult", "profound" or even "beautiful". These subjective judgments vary not only from person to person, but also over time and culture: for example, as a proof is obtained, simplified, or better understood, a once difficult theorem may become trivial. On the other hand, a profound theorem may be stated simply, but its proof may involve surprising and subtle connections between disparate areas of mathematics. Fermat's Last Theorem is a particularly well-known example of such a theorem.
Informal account of theorems
Logically, many theorems have the form of a conditional indicative: If A, then B. Such a theorem does not assert "B", only that "B" is a necessary consequence of "A". In this case, A is called the hypothesis of the theorem ("hypothesis" here means something quite different from a conjecture), and B the conclusion of the theorem. The two together (without the proof) are called the proposition or statement of the theorem (for example, "If A, then B" is the proposition). Alternatively, A and B can also be called antecedent and consequent, respectively. The "If Theorem n is an even natural number, so n/2 is a natural number" is a typical example where the hypothesis is "n is an even natural number", and the conclusion is "n/2 is also a natural number".
For a theorem to be proved, it must in principle be expressible as a formal and precise statement. However, theorems are usually stated in natural language rather than in a fully symbolic form, with the presumption that a formal statement can be derived from an informal one.
It is common in mathematics to choose a number of hypotheses within a given language and declare that the theory consists of all provable statements from these hypotheses. These hypotheses form the fundamental basis of the theory and are called axioms or postulates. The field of mathematics known as proof theory studies the formal languages, axioms, and structure of proofs.

Some theorems are "trivial," in the sense that they follow from definitions, axioms, and other theorems in an obvious way and contain no surprising insights. Some, on the other hand, can be called "deep," because their proofs can be long and difficult, involve areas of mathematics superficially dissimilar to the statement of the theorem itself, or show surprising connections between disparate areas of mathematics.. A theorem can be simple to state and yet be profound. An excellent example is Fermat's Last Theorem, and there are many other examples of simple but profound theorems in number theory and combinatorics, among other areas.
Other theorems have a known proof that cannot be easily written. The most prominent examples are the four color theorem and Kepler's conjecture. Both theorems are only known to be true by reducing them to a computational search that is then verified by a computer program. Initially many mathematicians did not accept this form of proof, but it has become more widely accepted. The mathematician Doron Zeilberger has even gone so far as to claim that these are possibly the only non-trivial results that mathematicians have ever proved. Many mathematical theorems can be reduced to simpler calculations, including polynomial identities, trigonometric identities, and identities hypergeometric.
Interlinked theorems
Being p and q two propositions, the following theorems are obtained, exchanging the hypothesis with the conclusion and then considering the negations of the original propositions.
Direct theorem: p⇒ ⇒ q{displaystyle pRightarrow q}
Reciprocal theorem: q⇒ ⇒ p{displaystyle qRightarrow p}
Inverse theorem:− − p⇒ ⇒ − − q{displaystyle -pRightarrow -q}
Counterreciprocal theorem: − − q⇒ ⇒ − − p{displaystyle -qRightarrow -p}
Mathematics Terminology
In mathematics a statement must be interesting or important within the mathematical community to be considered a theorem. The less important statements are called:
- Lema: an affirmation that is part of a wider theorem. Sometimes the slogans become so important that they become theorems, such as Gauss' motto and Zorn's motto, for example. These, by themselves, are theorems, although, for historical reasons, the word slogan remains in his name.
- Corolary: an affirmation that immediately follows a theorem. A proposal A is a corollary of a proposition or theorem B Yeah. A can be simply deduced from B.
- Proposed: an assertion or result not associated with any particular theorem. Many experts use proposition as a synonym for theorem.
- A conjecture or hypothesis, a mathematical statement that is supposed to be true, not yet proven. As long-standing examples: the conjecture of Goldbach or the Riemann hypothesis.
Theorems within other sciences
Frequently in physics or economics some important statements that can be deduced or justified from other basic statements or hypotheses are commonly called theorems. However, frequently the areas of knowledge where these statements appear have not been adequately formalized in the form of a logical system, so the term theorem should be used with caution to refer to these demonstrable or deductible statements. of "most basic" assumptions.
Design
A theorem and its proof are usually presented as follows:
- Theorem (name of the person who proved it, along with the year of discovery or publication of the test)
- Enunciado del theorem (sometimes called Proposed)
- Test
- Description of the test
- Fin
The end of the test can be marked with the letters Q.E.D. (quod erat demonstrandum) or with one of the tombstone marks, such as "□" or "∎", meaning "end of proof", introduced by Paul Halmos after its use in journals to mark the end of an article.
The exact style depends on the author or publication. Many publications provide instructions or macros for composing in the internal style.
It is common for a theorem to be preceded by a definition that describes the exact meaning of the terms used in the theorem. It is also common for a theorem to be preceded by a series of propositions or lemmas that are then used in the proof. However, lemmas are sometimes embedded in the proof of a theorem, either with nested proofs or with their proofs presented after the proof of the theorem.
Corollaries of a theorem occur between the theorem and the proof, or directly after the proof. Sometimes corollaries have proofs of their own that explain why they follow from the theorem.
Know
It has been estimated that more than a quarter of a million theorems are proven each year.
The well-known aphorism, "A mathematician is a device for turning coffee into theorems," is probably due to Alfréd Rényi, though it is often attributed to Rényi's colleague Paul Erdős (and Rényi may have been thinking of Erdős), who was famous for the many theorems he produced, the number of his collaborations, and his consumption of coffee.
Some consider the classification of finite simple groups to be the longest proof of a theorem. It comprises tens of thousands of pages in 500 journal articles by about 100 authors. These papers taken together are believed to provide a complete proof, and several ongoing projects hope to shorten and simplify this proof. Another such theorem is the four-color theorem whose computer-generated proof is too long for a human to read. human being. It is one of the longest known proofs of a theorem whose statement can be easily understood by a layman.
Famous theorems
Some of the best-known theorems are:
- Theorem of Pappus-Guldin
- Theorem of Pythagoras
- Bayes Theorem
- Theorem of the Binomial
- Nyquist-Shannon sampling theorem
- Gödel incompleteness theorem
- Theorem of the Central Limit
- Theorem of the prime numbers
- Theorem of Divergence
- Theorem of Bell
- Stokes Theorem
- Tales Theorem
- Theorem of Hilbert's zeros
- Frobenius Theorem
- Theorem of Fermat-Wiles
- Morley Theorem
- Shannon Theorem
- Theorem of the Bisectriz
- Middle Value Theorem
- Taylor Theorem
- Rolle Theorem
- Cauchy Theorem
Contenido relacionado
International System Prefixes
MathML
Stochastic