Thales's theorem

Tales of Mileto

There are two theorems related to classical geometry called Thales' theorem, both attributed to the Greek mathematician Thales of Miletus in the 6th century BC. c.

The two theorems of Thales

Semicircle that illustrates the second theorem of Tales

The first of them essentially explains a way to build a similar triangle from a previously existing one ("similar triangles are those with congruent angles, which means that their homologous sides are proportional and vice versa").

While the second unravels an essential property of the circumcenters of all right triangles ("these being at the midpoint of their hypotenuse"), in turn, in the geometric construction it is widely used to impose conditions for the construction of angles straight.

If various parallel lines are intersected by two transversals, the segments determined by the parallel lines and corresponding lines between transversals are proportional.

First Theorem

An application of the Tales Theorem

As a definition prior to stating the theorem, it is necessary to establish that two triangles are similar if they have equal corresponding angles or if their sides are proportional to each other. Thales's first theorem collects one of the most basic results of geometry, namely that:

Apparently, Thales discovered the theorem while investigating the condition of parallelism between two lines. In fact, Thales's first theorem can be stated as that the equality of the quotients of the sides of two triangles is not a sufficient condition of parallelism. However, the main application of the theorem, and the reason for its fame, derives from the establishment of the triangle similarity condition, from which the following corollary is obtained.

Application

From the establishment of the existence of a relationship of similarity between both triangles, the necessary proportionality between their sides is deduced. That means that the ratio between the lengths of two of them in one triangle remains constant in the other.

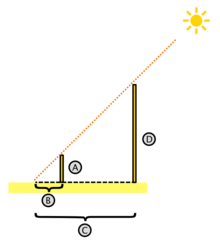
For example, in the figure we can see two triangles that, by virtue of Thales' theorem, are similar. Then, from it it follows as a corollary that the quotient between the sides A and B of the small triangle is the same as the quotient between the sides D and C in the large triangle. That is, since by Thales' theorem both triangles are similar, it is true that:

AB=DC{displaystyle {frac {A}{B}}={frac {D}{C}{,}}

This corollary is the basis of descriptive geometry. Its usefulness is evident; According to Herodotus, Thales himself used the corollary of his theorem to measure the height of the Cheops pyramid in Egypt. In any case, the theorem proves the similarity between two triangles, not the constancy of the quotient.

From Thales's first theorem, the following can also be deduced (actually it is another variant of said theorem, and, in turn, a consequence of it): If lines A, B, C are parallel and intersect two other lines R and S, then the segments that determine in them are proportional.

Second Theorem

Fig 2.1 Illustration of the statement of the second theorem of Tales de Mileto

The second theorem of Thales of Miletus is a geometry theorem particularly focused on right triangles, circles and inscribed angles, it consists of the following statement:

This theorem (see fig 2.1 and 2.2), is a particular case of a property of the cocyclic points and the application of inscribed angles within a circle.

Demo

Fig 2.2 Whenever AC be a diameter, the angle B will be constant and straight.

Fig 2.3 The triangles AOB and BOC They're isosceles.

In the circle with center O and radius r (see fig 2.3), the segments

OA, OB and OC

they are the same because they are all radii of the same circumference.

Therefore, the triangles AOB and BOC are isosceles.

The sum of the angles of triangle ABC is:

α α +β β +α α +β β =180 {displaystyle alpha +beta +alpha +beta ,=,180^{circ}}

2(α α +β β )=180 {displaystyle 2(alpha +beta),=,180^{circ }}}

Dividing both sides of the previous equation by two, we obtain:

α α +β β =90 {displaystyle alpha +beta ,=,90^{circ}}

With the previous expression the second theorem is proved.

Corollaries

Since applying the previous theorem, it is known that for any position adopted by the vertex B the equality holds, OA = OB = OC = r, where OB is the median of the hypotenuse, (see fig 2.3).

Corollary 2 also arises from applying the previous theorem, for an intuitive understanding it is enough to observe fig 2.2 '

Application of the second theorem

Tangent construction (red lines) to a circumference k from a point Pusing the "second Tales Theorem"

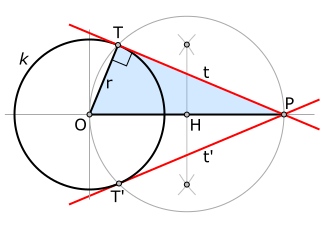
The «second theorem» (from Thales of Miletus) can be applied to draw the tangents to a given circle k, which also pass through a point P known and external to it (see figure).

Suppose that any tangent t (for now unknown) touches the circle k in a T point (also unknown for now). It is known by symmetry that any radius r of the circle k is perpendicular to the tangent of the point T that said radius defines in it, so it is concluded that angle OTP is necessarily right.

The above implies that the triangle OTP is a right triangle. Recalling “corollary 2 of the second theorem of Thales” we can deduce that then the triangle OTP is inscribable in a circle of radius ½ of the hypotenuse OP of the same.

Then marking the point H as the midpoint of the hypotenuse OP and centering on it, We can draw a second auxiliary circle (grey in the figure) that will circumscribe the triangle OTP.

This last drawn circle will intersect the circle k at two points T and T', these are precisely the points of tangency of the two lines that are simultaneously tangent to k and also pass through the point P, now known as the points T and T' just draw the lines TP and T'P (red in figure) to solve the problem.

Legend

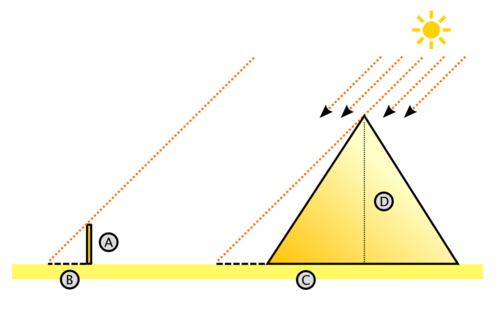
According to the legend related by Pliny the Elder in his Natural History, Thales managed to measure the Pyramid of Cheops at the time of day when an object measures the same as its own shadow.

Later, Plutarch, in his work Moralia, enriched the legend, reporting that at a fictitious dinner Thales is praised saying: «…with your method of measuring the pyramid, because, without making noise or needing any instrument, simply you place a rod in a vertical position at the edge of the shadow cast by the pyramid, and, the two triangles formed by the cutting of the sun's rays being equal, you showed that the height of the pyramid maintained the same relation to the length of the stick that shadow with the other… ».

The legend has been enriched in detail over time; one of the current versions is that Thales of Miletus, on a trip to Egypt, visited the pyramids of Giza (those of Cheops, Kefren and Menkaure), built several centuries before. Admired before such portentous monuments of this civilization, he wanted to know its height. According to the legend, he treated this problem with similarity of triangles (and under the assumption that the incident solar rays were parallel), he was able to establish a similarity relationship (Thales's first theorem) between two triangles rectangles, on the one hand the one with the legs (C and D) at the length of the shadow of the pyramid (knowable) and the length of its height (unknown), and on the other hand, using a stick (nailed into the ground perfectly vertically ) whose knowable legs (A and B) are the length of the rod and the length of its shadow. Taking the measurements at a time of day when the shadow of the rod is perpendicular to the base of the face from which the shadow of the pyramid was measured, and adding half the length of one of the faces to its shadow, he obtained the total length C from the shadow of the pyramid to the center of the pyramid.

As in such triangles, it is fulfilled that AB=DC{displaystyle {frac {A}{B}}}={frac {D}{C}{C}}, therefore the height of the pyramid is D=ACB{displaystyle D={frac {AC}{B}}}}which solved the problem.