Terrestrial magnetic field

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Computer simulation of the land field lines in a standard period between investments (success when the field points towards the center and yellow when it points out); the rotation axis of the earth is centered and vertical; the most complex distribution of lines corresponds to the liquid part of the Earth nucleus.

The terrestrial magnetic field (also called geomagnetic field), is the magnetic field that extends from the inner core of the Earth to space, where it meets the solar wind; a stream of energetic particles emanating from the Sun. The Earth's magnetic field can be approximated with the field created by a magnetic dipole (such as a bar magnet) tilted at an angle of 15 degrees to the Earth's axis of rotation.

Its magnitude at the Earth's surface varies from 25 to 65 µT (microteslas) or (0.25-0.65 G) being greater at the poles and less at the magnetic equator. This field is responsible for the compass needle being oriented pointing the same direction.

Earth's field changes over time in intensity and orientation because it is generated by the movement of molten iron alloys in the outer core of planet Earth (the geo-dynamo). For example, the magnetic north pole moves at a rate of 40 km/yr, slow enough for compasses to be useful in navigation.

After certain periods of random duration (with an average duration of several hundred thousand years), the Earth's magnetic field reverses (the geomagnetic north and south poles swap their positions). These inversions leave a record in the rocks that allow paleomagnetists to calculate the drift of continents in the past and the ocean floors resulting from plate tectonics.

The magnetic field interacts with the solar wind in a region called the magnetosphere that extends above the ionosphere, higher than 500 km and thousands of kilometers into space. This layer shields Earth from cosmic rays that would destroy the outer atmosphere, including the ozone layer that shields Earth from harmful ultraviolet radiation.

Importance

Earth is mostly shielded from the solar wind, a stream of energetic charged particles emanating from the Sun, by its magnetic field, which deflects most of the charged particles. These particles would destroy the ozone layer, which protects Earth from harmful ultraviolet rays. almost total removal of its atmosphere as a result of the turning off of the planet's magnetic field.

The polarity of Earth's magnetic field is recorded in igneous and sedimentary rocks. Reversals are detectable as bands centered on mid-ocean ridges where the ocean floor is spreading, while the stability of the geomagnetic poles between different reversal events allows paleomagnetists to track the drift of continents. Reversals also constitute the basis of magnetostratigraphy, a method of dating rocks and sediments. The field also magnetizes the crust; anomalies can be used to detect valuable mineral ores.

Humans have used compasses to orient themselves since the 11th century BCE. C., and for navigation from the XII century.

Main features

Description

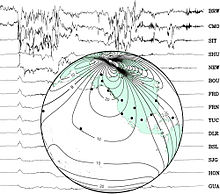
More used coordinate systems to represent the Earth's magnetic field.

The magnetic field can be represented at any point by a three-dimensional vector (see figure). A common way to measure your direction is to use a compass to determine the direction of magnetic north. Its angle with respect to geographic north is called declination. Pointing towards magnetic north, the angle that the field maintains with the horizontal is the inclination. The intensity (F) of the field is proportional to the force exerted on the magnet. You can also use a representation with XYZ coordinates in which X is the direction of the meridians (with a sense of geographic north), Y is the direction of the parallels (sense to the east) and Z is the vertical direction (with the sense downward pointing to the center of the Earth).

Intensity

Field strength is highest near the poles and lowest near the equator. It is frequently measured in Gauss (one ten-thousandth of a Tesla), but is usually represented using nanoteslas (nT), where 1 G = 100,000 nT. The nanotesla is also called a Gamma). The field varies between approximately 25,000 and 65,000 nT (0.25-0.65 G). By comparison, a fridge magnet has a field of 100 gauss.

Intensity of the Earth's magnetic field taken from the World Magnetic Model (World Magnetic Model o WMM) for 2010.

The intensity isoline maps are called isodynamic charts. In the image on the left you can see an isodynamic chart of the Earth's magnetic field. The intensity minimum occurs over South America, while the maximum occurs over northern Canada, Siberia, and the coast of Antarctica south of the Australian continent.

Tilt

Inclination of the Earth's magnetic field from WMM data for 2010.

The inclination is given by the angle by which the field points downwards with respect to the horizontal. It can have values between -90º (upwards) and 90º (downwards). At the magnetic north pole, it points completely downwards, and progressively rotates upwards as latitude decreases to the horizontal (inclination 0º), which is reached at the magnetic equator. It continues to rotate until it reaches the vertical at the south magnetic pole. Tilt can be measured with a tilt circle.

A map of Earth's tilt isolines is shown in the figure to the right.

Declension

Main article: Magnetic decline

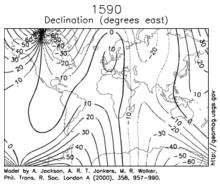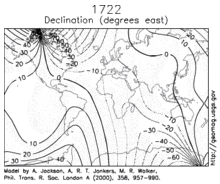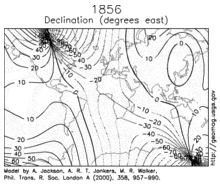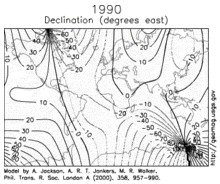
Declination is positive for an easterly field deviation relative to geographic north. It can be estimated by comparing the bearing of a compass with the position of the celestial pole. Maps typically include declination information as a small diagram showing the relationship between magnetic and true north. Declination information for a region can be represented by an isogonic chart (map of isolines joining points with the same declination).

Earth's magnetic field decline from the 2010 WMM. Isogonic lines offer declination in degrees.

An isogonic chart of the earth's magnetic field is shown in the image on the left.

Dipolar approximation

Near the Earth's surface, its magnetic field can be reasonably approximated by that created by a magnetic dipole located in the center of the Earth and inclined at an angle of 11.5º with respect to the axis of rotation of the Earth. planet. The dipole is approximate to a bar magnet, with the south pole pointing toward the geomagnetic north pole. The north pole of a magnet is defined by the attraction towards the north pole of the Earth. Based on the fact that the north pole of a magnet attracts the south pole of other magnets and repels the north poles, it must be attracted to the south pole of the Earth magnet. This dipole field accounts for about 80-90% of the total field in most locations.

Magnetic Poles

The motion of the magnetic north pole of the Earth along the Canadian Arctic.

The position of the magnetic poles can be defined in at least two ways. A magnetic tilt pole is a point on the Earth's surface whose magnetic field is totally vertical.

The inclination of the Earth's field is 90º at the north magnetic pole and -90º at the south magnetic pole. The two poles move independently of each other and are not located perfectly facing each other at opposite points on the globe. Its movement can be fast: movements of the magnetic north pole have been detected in excess of 40 km per year. Over the past 180 years, the magnetic north pole has been migrating northwestward, from Cape Adelaide on the Boothia Peninsula in 1831 to Resolute Bay 600 km away in 2001. The magnetic equator is the curve of zero level (magnetic field is horizontal).

If a line is drawn parallel to the moment of the dipole that is closest to the Earth's magnetic field, the points of intersection with the Earth's surface are called the geomagnetic poles. That is, the geomagnetic north and south poles would be equivalent to the magnetic north and south poles if the Earth were a perfect dipole. However, the Earth's field has a significant contribution from non-dipole terms, so the poles do not coincide.

Magnetosphere

Main article: Magnetosphere of the Earth

A good part of the charged particles coming from the solar wind are trapped in the Van Allen belts. A small number of particles from the solar wind manage to reach, following a magnetic field line, up into the upper atmosphere and ionosphere in the auroral zones. The only time the solar wind is observable from Earth is when it is strong enough to produce phenomena such as auroras and geomagnetic storms. Auroras of a certain magnitude in terms of brightness noticeably heat the ionosphere, causing its plasma to expand into the magnetosphere, increasing the size of the plasma geosphere, and causing mass to escape from the atmosphere in the solar wind. Geomagnetic storms occur when the pressure of the plasmas contained within the magnetosphere is great enough to swell and consequently distort the geomagnetic field.

Simulation of the interaction between the terrestrial magnetic field and the interplanetary magnetic field. The magnetosphere is compressed into the "day part" facing the Sun, due to the action of the particles that come and spreads in the "night side".

The solar wind is responsible for the average shape of Earth's magnetosphere. Fluctuations in its speed, density, and direction greatly affect the planet's local environment. For example, levels of ionizing radiation and low frequency interference can vary by factors of hundreds to thousands; the shape and location of the magnetopause and shock wave (on the upstream side) can vary over several Earth radii, exposing geosynchronous satellites to the effects of direct solar wind. These phenomena are collectively known as space weather. The detachment and loss of atmospheric mass procedure is caused when gas is trapped in magnetic field bubbles, which are blown away by the solar wind. In addition, variations in magnetic field strength have been correlated with variation in precipitation. in the tropics.

Time dependency

Short-term variations

Fund: A group of magnetic observatory measures showing a magnetic storm in 2000.
Earth balloon: Map showing locations of different observatories and horizontal field intensity isolines in μT units.

The geomagnetic field changes on time scales from milliseconds to millions of years. The smallest time scales are given from the fluxes in the ionosphere (the ionosphere dynamo) and the magnetosphere; some of these changes can be made to correspond to geomagnetic storms or daily variations in currents. Changes on time scales longer than one year reflect changes in the Earth's interior, particularly in the iron-rich core.

The Earth's magnetosphere is frequently impacted by solar flares that cause geomagnetic storms, the result of which are auroras. The short-term instability of the field is measured by the K-index.

Data collected by THEMIS show that the magnetic field, which interacts with the solar wind, decreases when the orientation of the magnetic field is aligned between the Sun and the Earth, in contradiction with previous hypotheses. In the course of solar storms, this could lead to blackouts and various damage to artificial satellites.

Secular variation

Estimated variation of the declination isolines between 1590 and 1990 (click to view animation).

Changes in the Earth's magnetic field on time scales of one year or longer are called secular variation. Over hundreds of years, the magnetic declination has been observed to vary by tens of degrees. The animation on the right shows how the declination has changed over the centuries.

The direction and intensity of the dipole changes with time. In the last two centuries the strength of the dipole has been decreasing at a rate of 6.3% per century. With this rate of decrease the field would vanish in 1,600 years. However, this intensity is similar to the average for the last two centuries. past 7,000 years, and the current rate of change is not anomalous.

A notable feature of the non-dipolar component of the secular variation is the westward drift at a rate of about 0.2º per year. This drift is not equal at all points and has varied over time. Average global trawl has been west since 1400 AD. C. but towards the east between the year 1000 and 1400 d. C.

Changes prior to magnetic observatory measurements are recorded in archaeological and geological materials. These changes are called paleomagnetic secular variation or paleosecular variation. These records typically include long periods of small variations with large point changes that reflect geomagnetic reversals and geomagnetic excursions ("sudden" breaks in the field not coupled with a subsequent reversal, but return to initial polarity).

Field Inversions

Main article: Magnetic investment

Although the Earth's magnetic field is generally well approximated by a magnetic dipole with its axis close to that of rotation, dramatic events occasionally occur where the geomagnetic north and south poles are swapped. These events are called geomagnetic reversals. Evidence for these events is found in basalts, core sediments obtained from the ocean floor, and from seafloor magnetic anomalies. The reversals occur at seemingly random time intervals ranging from less than 100,000 years up to 50 million years. The most recent event, called the Brunhes-Matuyama inversion, occurred 780,000 years ago.

Geomagnetic polarity during the end of the Cenozoic era. The dark-colored zones denote periods in which the polarity coincided with the current, while the light-colored zones denote inverted polarity periods.

A study published in 2012 by the German Research Center for Earth Sciences suggests that a brief reversal occurred only 41,000 years ago during the last ice age.

The history of the magnetic field is recorded mainly in iron oxides such as magnetite, which have ferromagnetic properties, or other types of structures that can be magnetized by the Earth's magnetic field. Remanent magnetization, or remanence, can be acquired in more than one way. In lava flows, the direction of the field freezes into small magnetic particles as they cool, causing thermoremanent magnetization. In sediments, the orientation of the particles acquires a certain tendency towards the direction of the field when they are deposited on an ocean floor or on the bottom of a lake. This process is called remnant detrital magnetization.

Thermo-remanent magnetization is the form of remanence that causes magnetic anomalies in mid-ocean ridges. As the seafloor spreads, magma emanates from the mantle and would cool to form new basaltic crust. During cooling, the basalt guards the direction of the earth's field. This new basalt forms on both sides of the ridge and moves away from it. When the earth's magnetic field is reversed, the new basalt records the reverse direction. The result is a series of bands that are symmetrical around the ridge. A ship towing a magnetometer at the ocean surface can detect these bands and infer the age of the seafloor. This circumstance makes it possible to extract information from the rate at which the seabed has expanded over time.

Radiometric dating of lava flows has been used to calibrate a time scale of geomagnetic polarity, part of which is shown in the image to the left. This is the basis of magnetostratigraphy, a geophysical correlation technique that can be used to estimate the age of both sedimentary and volcanic rocks as well as ocean floor anomalies.

Studies of lava flows in the Steens Mountains, Oregon, indicate that the magnetic field may have moved at a very rapid rate, in excess of 6 degrees per day at a time of magnetic reversal.

Temporary dipole tilts that shift the dipole axis to the equator and then back to the original polarity—note that without actually reversing—are known as "excursions."

First appearance

A paleomagnetic study carried out on Australian red dacite and cushion lava suggests an estimate that the magnetic field has existed for at least 3.45 billion years.

Future

Variations of the virtual axis of the dipolo since the last investment.

Currently the average value of the geomagnetic field is decreasing; this deterioration corresponds to 10-15% of the total decline in the last 150 years and has accelerated in recent years. The geomagnetic intensity has decreased almost continuously from a maximum of 35% above the current value since 2000 years ago. The rate of decline and current intensity are within the normal range of variation, as shown by information from previous rock-recorded field values (figure to the right).

The nature of the Earth's magnetic field is that of a heteroscedastic fluctuation. An instantaneous measurement of it—or several measurements over decades or centuries—is not enough to extrapolate a general trend in field strength. This has risen and fallen in the past for no apparent reason. Furthermore, indicating the local intensity of the dipole field (or its fluctuation) is not enough to characterize the Earth's magnetic field as a whole, since it is not strictly a dipole field. The dipole component of this can decrease as the total magnetic field is maintained or its magnitude increases.

The Earth's magnetic north pole is moving from northern Canada to Siberia at a rapid rate: 10 km per year at the turn of the century XX, and in 2003 above 40 km per year; since then it has been accelerating.

Physical origin

Earth's core and geodynamo

It illustrates the relationship between the movement of the conductor fluid, organized in rolls by the force of Coriolis, and the magnetic field that the movement generates.

The Earth's magnetic field is mainly produced by electric currents that occur in the outer core, of a liquid nature, which is composed of highly conductive cast iron and nickel. The magnetic field is generated by forming a current line in a closed loop (Ampère's Law); a changing magnetic field generates an electric field (Faraday's Law); and the electric and magnetic fields exert a force on the charges flowing in the current (the Lorentz Force). These effects can be combined into a partial differential equation for the magnetic field called the "magnetic induction equation":

{frac {partial {mathbf {B}}}{partial t}}=eta nabla ^{2}{mathbf {B}}+nabla times ({mathbf {u}}times {mathbf {B}})

Where u It's fluid speed, B It's the magnetic field, and GEN=1/σμ is the magnetic diffusivity, being σ the electrical conductivity and μ permeability. The term of the left side of the equation represents the explicit temporal variation of the field, $nabla ^{2}$ is the operator of Laplace and $nabla times$ It's the rotational operator.

The first term on the right hand side of the equation represents a "diffusion" component. In a stationary fluid the magnetic field decreases and the field concentrations spread out. If the terrestrial dynamo were turned off the dipole component would disappear in a few tens of thousands of years.

Note that in a perfect conductor (conductivity σ=∞) there would be no diffusion. According to Lenz's law, any change in the magnetic field would be instantly counteracted by currents, so the flux through a given volume of fluid could not change. As the fluid moved, the magnetic field would move with it. The theorem that describes this effect is called the "Frozen Flow Theorem." Even in a fluid with finite conductivity, a new field would be generated in the stretching of the field lines by moving the fluid in a way that deforms it. This process could continue to generate a field indefinitely, if it were not for the fact that by increasing its intensity, it opposes the movement of the fluid.

The movement of the fluid is maintained by convection —movement based on buoyancy. The temperature increases towards the center of the Earth, and the greater the temperature of the fluid at greater depths the lighter it becomes. This buoyancy is accentuated by chemical separation. As the core cools, some of the molten iron solidifies and sticks to the inner core. In the process, lighter elements remain in the fluid, making it less dense. That's called "positional convection." The Coriolis force, a consequence of the planet's rotation, tends to organize the fluid in coils aligned in the direction of the north-south polar axis.

The simple convective movement of a conducting fluid is not enough to guarantee the generation of a magnetic field. The model explained above assumes the movement of charges (such as electrons with respect to the atomic nucleus), which is a requirement to generate a magnetic field. However, it is not clear how this movement of charges arises in the fluid circulating in the outer core. Possible mechanisms that would explain this include electrochemical reactions that create the equivalent of a battery by generating electrical current in the fluid, or a thermoelectric effect (both of which are somewhat outdated). Remaining magnetic fields in mantle magnetic materials, which are colder than their Curie temperature, would also provide starting "stator" magnetic fields, which would induce the required currents in the convective flow of the fluid behaving like a dynamo. These mechanisms were analyzed by Philip William Livermore.

The average magnetic field in Earth's outer core was calculated to be around 25 G, 50 times greater than the field at the surface.

In 2016, a research team from the National Center for Scientific Research (CNRS) and the Blas Pascal University proposed another mechanism involved in maintaining the movements of metallic fluids inside the planet. This mechanism is the effect of tidal forces caused by the Moon, which not only cause the oceans to bulge, but also elastically deform the Earth's mantle. This deformation could continuously stimulate the movement of the liquid iron alloy that makes up the outer core and thus generate the Earth's magnetic field.

Numerical models

The geodynamo equations are extremely complex to solve, and the realism of the solutions is limited mainly by the computing power. For decades theorists were limited to creating kinematic dynamos, in which the velocity of the fluid is prescribed in advance of calculating the effect of the magnetic field. Kinematic dynamo theory was essentially a matter of trying different geometries of the flow and seeing if it could be adapted to a dynamo.

The first self-consistent dynamo models, those that determine both the velocity of the fluid and the magnetic field, were developed by two groups in 1995, one in Japan and one in the United States. The latter received much attention because successfully managed to reproduce some of the features of the Earth's field, including geomagnetic reversals.

Currents in the ionosphere and magnetosphere

Induced electrical currents in the ionosphere generate magnetic fields (ionospheric dynamo region). This type of field is always generated in the area where the atmosphere is closest to the Sun, and causes daily disturbances that can alter the magnetic fields on the surface by up to 1º. Typical daily variations in field strength are around 25 nT, with seconds-scale variations on the order of 1 nT.

Crustal magnetic anomalies

Model for lower wavelength components of the terrestrial magnetic field, attributed to anomalies in the lithosphere.

Magnetometers detect deviations in the Earth's magnetic field caused by iron artifacts, some types of stone structures, and even trenches and archaeological sites. The use of instruments adapted from airborne detectors was developed during World War II to detect submarines, and the magnetic variations of the ocean floor have been mapped. Basalt, the iron-rich volcanic rock that makes up most of the ocean floor, contains a strongly magnetic mineral (magnetite) and can distort compass readings at a local level. This distortion was detected by Icelandic sailors as early as the end of the 18th century. More importantly, due to the presence of magnetite, which provides the basalt with measurable magnetic qualities, these magnetic variations provide another means of studying the ocean floor. When the newly created rock cools, the magnetic materials record the Earth's magnetic field at that precise moment.

Measurement and analysis

Detection

The strength of the magnetic field was first measured by Carl Friedrich Gauss in 1835 and has been measured numerous times since then, showing a relative decay of around 10% over the last 150 years. The Magsat satellite and later other satellites have used three-axis magnetometers to probe the three-dimensional structure of Earth's magnetic field. The Ørsted satellite pointed to a geodynamo-dynamics at work that appears to be causing an alternate pole to emerge under the Atlantic Ocean west of South Africa.

Units operated by various governments specialized in measuring the Earth's magnetic field are called geomagnetic observatories, often part of a national geological research department, for example the Eskdalemuir observatory of the British Department of Geological Research ( British Geological Survey). These observatories are capable of measuring and predicting the magnetic conditions that, in the form of magnetic storms, frequently alter telecommunications, electric power and other human activities.

Different military forces determine the characteristics of the local geomagnetic field in order to detect anomalies that could be caused by a relevant metallic object —such as a submerged submarine. These magnetic anomaly detectors are used on aircraft such as the British Nimrod or towed as instruments on ships.

In the commercial field, geophysical prospecting companies also use magnetic detectors to identify anomalies produced by economically interesting mineral ores, such as the Kursk magnetic anomaly.

Statistical models

Each measurement of the magnetic field is taken at a particular time and place. If an accurate estimate of the field at other places and times is required, the measurements must be converted to a valid model to make predictions.

Spherical harmonics

See also: Spherical harmonics and Multipolar development.

Schematic representation of spherical harmonics on a sphere and its nodal lines. Function P_lm It's null in. m circles that pass through the poles and in the circles of equal latitude. The function changes as a sign every time one of these lines is crossed.

Example of quadrupolar field. It can also be built by putting together two dipolos. If this arrangement was placed in the center of the Earth, then a scientific research on the surface would discover two magnetic north poles (in the geographical poles) and two south poles in the equator.

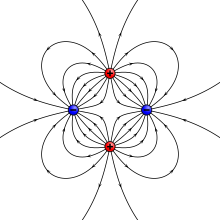
The most common way to analyze the global variations of the Earth's magnetic field is to fit the measurements to a group of spherical harmonics. This method was first used by Carl Friedrich Gauss. Spherical harmonics are functions that oscillate on the surface of a sphere. They are the product of two angular functions, one that depends on latitude and the other on longitude. The function dependent on longitude is zero in a certain number of circles that pass through the north and south poles; the number of said nodal lines is the absolute value of order m (or n, depending on the source). The number of circles of latitude in which the latitude function vanishes is equal to the order ℓ. Each harmonic is equivalent to a certain arrangement of magnetic charges in the center of the Earth. A monopole is an isolated magnetic charge, a phenomenon that has never been observed. A dipole is the equivalent of two close opposite charges and a quadrupole two dipoles together. An example of a quadrupole field is shown in the figure below to the right.

Spherical harmonics can represent any scalar field that satisfies certain properties. The magnetic field is a vector field, but if it is expressed in XYZ Cartesian components, each component is the derivative of the same scalar function called the magnetic potential. Analyzes of the Earth's magnetic field use a modified version of current spherical harmonics that differ by a multiplicative factor. The settings of the magnetic field measurements break down the Earth's magnetic field to a sum of spherical harmonics, each multiplied by the Gauss coefficient (g_m^ℓ or h_m^ℓ) more appropriate.

The lowest order Gaussian coefficient g₀⁰, which provides the contribution of an isolated magnetic charge, is therefore zero (no magnetic monopoles have been detected). The following terms (g₀¹, g₁¹ and h₁¹) determine the direction and intensity of the dipole contribution; the dipole setting is tilted at an angle of 10° to the axis of rotation, as described above.

Radial dependency

Spherical harmonic analysis can be used to differentiate external and internal contributions to the field when measurements are available at more than one altitude (eg, surface observatories and satellites). In this case, each coefficient term g_m^ℓ or h_m^ℓ can be decomposed into two terms: one that decreases with radius by a factor 1/r^ℓ+1 and another that increases with radius by r^ℓ. The increasing terms are those that adjust to external sources (currents in the ionosphere and magnetosphere). However, the time average of these contributions over a few years is zero.

The rest of the terms predict that the potential of a dipole source (ℓ=1) decays with 1/r³. The magnetic field, which is a derivative of the potential, therefore falls with 1/r³. Quadrupole terms fall with 1/r⁴. The rest of the higher order components decay with a progressively faster order with radius. The radius of the outer core is about half the Earth's radius. If the field at the core-mantle boundary is adjusted to spherical harmonics, the dipole component is smaller by a factor of 1/8 than that at the surface. By various arguments, it is usually assumed that only terms of order 14 or lower have their origin in the kernel. These terms have wavelengths of 2000 km or less. The rest of the smaller magnitude components are attributed to anomalies in the crust.

Global models

The International Association for Geomagnetism and Aeronomy uses a standard global field model called the International Geomagnetic Reference Field. It is updated every five years. The eleventh generation model, IGRF11, was developed using data from satellites (Ørsted, CHAMP and SAC-C) and from a worldwide network of geomagnetic observatories. The development in spherical harmonics was truncated in order 10, with 120 coefficients, until the year 2000. Models after this date have been truncated by a degree 13 (195 coefficients).

Another global field model is produced jointly by the US National Geophysical Data Center and the British Geological Survey. This model is truncated in order 12 (168 coefficients). It is used by the United States Department of Defense, the British Ministry of Defense, NATO and the International Hydrographic Office, as well as by multiple civil navigation systems.

A third model, produced by the Goddard Space Flight Center (NASA and GSFC) and the Danish Institute for Space Research, employs "thorough modelling" that tries to reconcile data of widely different temporal and spatial resolution obtained on the surface and from satellite sources.

Biomagnetism

Main article: Magnetorreception

There are animals, including several species of birds and turtles, that can detect the Earth's magnetic field and use it to orient themselves during their migrations. Cows and deer tend to align their bodies in a northerly direction -south when resting, but not when near power lines; this has led researchers to believe that the magnetism produced is responsible.

References and bibliography

↑ a b Glatzmaier, Gary A.; Roberts, Paul H. (1995). «A three-dimensional self-consistent computer simulation of a geomagnetic field reversal». Nature (in English) 377 (6546): 203-209. Bibcode:1995Natur.377..203G. doi:10.1038/377203a0.
↑ Glatzmaier, Gary. «The Geodynamo» (in English). University of California Santa Cruz. Consultation on October 2011.
↑ (in English)Quirin Shlermeler (3 March 2005). «Solar wind hammers the ozone layer». News@nature. doi:10.1038/news050228-12. Consultation on 27 September 2011.
↑ Luhmann, Johnson and Zhang, 1992
↑ a bc McElhinny, Michael W.; McFadden, Phillip L. (2000). Paleomagnetism: Continents and Oceans. Academic Press. ISBN 0-12-483355-1.
↑ (in English) Opdyke, Neil D.; Channell, James E. T. (1996). Magnetic Stratigraphy. Academic Press. ISBN 978-0-12-527470-8.
↑ (in English) Mussett, Alan E.; Khan, M. Aftab (2000). Looking into the Earth: An introduction to Geological Geophysics. Cambridge University Press. ISBN 0-521-78085-3.
↑ Temple, Robert (2006). The Genius of China. Andre Deutsch. ISBN 0-671-62028-2.
^ a b c d e f h i j Merrill, Ronald T.; McElhinny, Michael W.; McFadden, Phillip L. (1996). The magnetic field of the earth: paleomagnetism, the core, and the deep mantle. Academic Press. ISBN 978-0-12-491246-5.
↑ (in English) These are the units of a magnetic B-field. The magnetic H-field has different units, but outside of the Earth's core they are proportional to each other.
↑ (in English) National Geophysical Data Center. "Geomagnetism Frequently Asked Questions". Geomagnetism. NOAA. Consultation on October 2011.
↑ Campbell, 2003, p. 7
↑ Palm, Eric (2011). «Tesla». National High Magnetic Field Laboratory. Archived from the original on March 21, 2013. Consultation on October 2011.
↑ Guillermo Sánchez León (5 July 2016). «The sky of the Southern Hemisphere in the naked eye». Naukas.
↑ Campbell, Wallace A. (1996). "Magnetic" pole locations on global charts are incorrect." Eos, Transactions, American Geophysical Union 77 (36): 345. Bibcode:1996EOSTr..77..345C. doi:10.1029/96EO00237. Archived from the original on August 17, 2012. Consultation on 24 March 2013.
↑ Woods Hole Oceanographic Institution (ed.). «Ocean bottom magnetology laboratory». Archived from the original on 19 August 2013. Consultation on June 2012.
↑ "Earth's Inconstant Magnetic Field". NASA Science-Science News (in English). 29 December 2003. Archived from the original on February 1, 2010. Consultation on September 2011.
↑ «Solar wind ripping chunks off Mars». Cosmos Online. 25 November 2008. Archived from the original on 27 April 2012. Consultation on September 2011.
↑ National Environment Research Council, ed. (20 January 2009). «Link found between tropical rainfall and Earth's magnetic field». Planet Earth Online. Archived from the original on July 3, 2012. Consultation on 19 April 2012.
↑ NOAA - Space Weather Prediction Center (ed.). "The K-index." Archived from the original on October 22, 2013.
↑ Steigerwald, Bill (December 16, 2008). "Sun Often "Tears Out A Wall" In Earth's Solar Storm Shield. NASA, ed. THEMIS: Understanding space weather (in English). Consultation on 20 August 2011.
↑ Jackson, Andrew; Jonkers, Art R.T.; Walker, Matthew R. (2000). «Four centuries of Geomagnetic Secular Variation from Historical Records». Philosophical Transactions of the Royal Society A (in English) 358 (1768): 957-990. Bibcode:2000RSPTA.358..957J. JSTOR 2666741. doi:10.1098/rsta.2000.0569.
↑ a b Canadian Geological Survey, ed. (2011). «Secular variation». Geomagnetism (in English). Archived from the original on 25 July 2008. Consultation on 18 July 2011.
↑ Constable, Catherine (2007). «Dipole Moment Variation». In Gubbins, David; Herrero-Bervera, Emilio, eds. Encyclopedia of Geomagnetism and Paleomagnetism (in English). Springer-Verlag. pp. 159-161. ISBN 978-1-4020-3992-8. doi:10.1007/978-1-4020-4423-6_67.
↑ Dumberry, Mathieu; Finlay, Christopher C. (2007). «Eastward and westward drift of the Earth's magnetic field for the last three millennia». Earth and Planetary Science Letters (in English) 254: 146-157. Bibcode:2007E fakePSL.254..146D. doi:10.1016/j.epsl.2006.11.026.
↑ Tauxe, 1998, Ch. 1
↑ Merrill, McElhinny and McFadden, 1996, Chapter 5
↑ «Ice Age Polarity Reversal Was Global Event: Extremely Brief Reversal of Geomagnetic Field, Climate Variability, and Super Volcano» (in English). Sciencedaily.com. 16 October 2012. doi:10.1016/j.epsl.2012.06.050. Consultation on 21 March 2013.
↑ Coe, R.S.; Prévot, M.; Camps, P. (20 April 1995). «New evidence for extraordinarily rapid change of the geomagnetic field during a reversal». Nature (in English) 374 (6524): 687. Bibcode:1995Natur.374..687C. doi:10.1038/374687a0.
↑ McElhinney, T. N. W.; Senanayake, W. E. (1980). «Paleomagnetic Evidence for the Existence of the Geomagnetic Field 3.5 Ga Ago». Journal of Geophysical Research 85: 3523. Bibcode:1980JGR....85.3523M. doi:10.1029/JB085iB07p03523. Archived from the original on 29 July 2013. Consultation on 25 March 2013.
↑ Usui, Yoichi; Tarduno, John A., Watkeys, Michael, Hofmann, Axel, Cottrell, Rory D. (2009). «Evidence for a 3.45-billion-year-old magnetic remanence: Hints of an ancient geodynamo from conglomerates of South Africa». Geochemistry Geophysics Geosystems 10 (9). Bibcode:2009GGGG....1009Z07U. doi:10.1029/2009GC002496. The reference uses the obsolete parameter |coauthors= (help)
↑ Tarduno, J. A.; Cottrell, R. D., Watkeys, M. K., Hofmann, A., Doubrovine, P. V., Mamajek, E., Liu, D., Sibeck, D. G., Neukirch, L. P., Usui, Y. (4 March 2010). "Geodynamo, Solar Wind, and Magnetopause 3.4 to 3.45 Billion Years Aug". Science 327 (5970): 1238-1240. Bibcode:2010Sci...327.1238T. PMID 20203044. doi:10.1126/science.1183445. The reference uses the obsolete parameter |coauthors= (help)
↑ "Earth's Inconstant Magnetic Field". Archived from the original on February 1, 2010. Consultation on 7 January 2011.
↑ Lovett, Richard A. (24 December 2009). «North Magnetic Pole Moving Due to Core Flux».
^ a b c d Merrill, McElhinny and McFadden, 1996, Chapter 8
↑ Buffett, B. A. (2000). «Earth's Core and the Geodynamo». Science (in English) 288 (5473): 2007-2012. Bibcode:2000Sci...288.2007B. doi:10.1126/science.288.5473.2007.
↑ «Magnetic Stability Analysis for the Geodynamo» (in English). Consultation on December 2012.
↑ Buffett, Bruce A. (2010). «Tidal dissipation and the strength of the Earth's internal magnetic field». Nature (in English) 468 (7326): 952-954. Bibcode:2010Natur.468..952B. PMID 21164483. doi:10.1038/nature09643. Archived from the original on December 22, 2010. Disclosure summary – Science 20.
↑ Fernando Ballesteros (18 April 2016). "The Moon played a major role in maintaining the Earth's magnetic field." Observatori Astronomic - Universitat de Valencia.
↑ «The Moon thought to play a major role in maintaining Earth's magnetic field». National Center for Scientific Research (in English). 31 March 2016. Consultation on September 8, 2018.
↑ a b Kono, Masaru; Paul H. Roberts (2002). «Recent geodynamo simulations and observations of the geomagnetic field». Reviews of Geophysics (in English) 40 (4): 1-53. Bibcode:2002RvGeo..40.1013K. doi:10.1029/2000RG000102. The reference uses the obsolete parameter |coauthors= (help)
↑ Kageyama, Akira; Sato, Tetsuya, the Complexity Simulation Group, (1 January 1995). «Computer simulation of a magnetohydrodynamic dynamo. II». Physics of Plasmas (in English) 2 (5): 1421-1431. Bibcode:1995PhPl....2.1421K. doi:10.1063/1.871485. The reference uses the obsolete parameter |coauthors= (help)
↑ Glatzmaier, G; Paul H. Roberts (1995). «A three-dimensional convective dynamo solution with rotating and finitely conducting inner core and mantle». Physics of the Earth and Planetary Interiors (in English) 91 (1–3): 63-75. doi:10.1016/0031-9201(95)03049-3. The reference uses the obsolete parameter |coautores= (help)
↑ Stepišnik, Janez (2006). "Spectroscopy: NMR down to Earth". Nature 439 (7078): 799-801. Bibcode:2006Natur.439..799S. doi:10.1038/439799a.
↑ Frey, Herbert. "Satellite Magnetic Models". Comprehensive Modeling of the Geomagnetic Field. NASA. Consultation on 13 October 2011.
↑ Courtillot, Vincent; Le Mouël, Jean Louis (1988). «Time Variations of the Earth's Magnetic Field: From Daily to Secular». Annual Review of Earth and Planetary Science (in English) 1988 (16): 435. Bibcode:1988AREPS..16..389C. doi:10.1146/annurev.ea.16.050188.002133.
↑ Hulot, G.; Eymin, C.; Langlais, B.; Mandea, M.; Olsen, N. (April 2002). «Small-scale structure of the geodynamo inferred from Oersted and Magsat satellite data». Nature (in English) 416 (6881): 620-623. PMID 11948347. doi:10.1038/416620a. The reference uses the obsolete parameter |month= (help)
↑ Deutschlander, M.; Phillips, J.; Borland, S. (1999). «The case for light-dependent magnetic orientation in animals». Journal of Experimental Biology (in English) 202 (8): 891-908. PMID 10085262.
↑ Burda, H.; Begall, S.; Cerveny, J.; Neef, J.; Nemec, P. (Mar 2009). «Extremely low-frequency electromagnetic fields disrupt magnetic alignment of ruminants». Proceedings of the National Academy of Sciences of the United States of America (in English) 106 (14): 5708-5713. Bibcode:2009PNAS.106.5708B. PMC 2667019. PMID 19299504. doi:10.1073/pnas.0811194106. The reference uses the obsolete parameter |month= (help)
↑ Dyson, P. J. (2009). "Biology: Electric cows". Nature (in English) 458 (7237): 389. Bibcode:2009Natur.458Q.389.. PMID 19325587. doi:10.1038/458389a.

Additional bibliography

Campbell, Wallace H. (2003). Introduction to geomagnetic fields (in English) (2nd edition). New York: Cambridge University Press. ISBN 978-0-521-52953-2.
Comins, Neil F. (2008). Discovering the Essential Universe (in English) (Fourth edition). W. H. Freeman. ISBN 978-1-4292-1797-2.
Love, Jeffrey J. (2008). «Magnetic monitoring of Earth and space». Physics Today (in English) 61 (2): 31-37. Bibcode:2008PhT....61b..31H. doi:10.1063/1.2883907.
Merrill, Ronald T. (2010). Our Magnetic Earth: The Science of Geomagnetism (in English). University of Chicago Press. ISBN 0-226-52050-1.
Merrill, Ronald T.; McElhinny, Michael W.; McFadden, Phillip L. (1996). The magnetic field of the earth: paleomagnetism, the core, and the deep mantle (in English). Academic Press. ISBN 978-0-12-491246-5.
«Temperature of the Earth's core». NEWTON Ask a Scientist (in English). 1999. Archived from the original on September 8, 2010. Consultation on September 2011.
Tauxe, Lisa (1998). Paleomagnetic Principles and Practice (in English). Kluwer. ISBN 0-7923-5258-0.
Towle, J. N. (1984). «The Anomalous Geomagnetic Variation Field and Geoelectric Structure Associated with the Mesa Butte Fault System, Arizona». Geological Society of America Bulletin (in English) 9 (2): 221-225. doi:10.1130/0016-7606(1984)95 vis221:TAGVFA student2.0.CO;2.
Wait, James R. (1954). «On the relation between telluric currents and the earth's magnetic field». Geophysics (in English) 19 (2): 281-289. Bibcode:1954Geop...19..281W. doi:10.1190/1.1437994.
Martin, Walt (1994). Introduction to Geomagnetically Trapped Radiation (in English). Cambridge University Press. ISBN 978-0-521-61611-9.

Contenido relacionado

Más resultados...