Taylor's theorem

ImprimirCitar

The exponential function

{displaystyle y={text{e}}^{x}}

(continuous red line) and its approach through a Taylor polynomial around the origin of coordinates (continuous green line)

In differential calculus, Taylor's theorem, is named after the British mathematician, Brook Taylor, who stated it more generally in 1712, although James Gregory had previously discovered it in 1671. Theorem allows us to obtain polynomial approximations of a function in a neighborhood of a certain point in which the function is differentiable. In addition, the theorem allows us to delimit the error obtained by said estimation.

Instance of a variable

Statement of the theorem

The most basic version of the theorem is as follows:

Taylor's Theorem.Sea k 한 N and be f: R → R a differential function k times at the point a 한 R. Then there is a function h_k: R → R such as
(1) ${displaystyle f(x)=f(a)+f'(a)(x-a)+{frac {f''(a)}{2!}}(x-a)^{2}+cdots +{frac {f^{(k)}(a)}{k!}}(x-a)^{k}+h_{k}(x)(x-a)^{k},}$
with ${displaystyle quad lim _{xto a}h_{k}(x)=0}$ . This is the call. shape of Peano of the rest.

Brook Taylor

The polynomial that appears in Taylor's theorem,

{displaystyle P_{k}(x)=f(a)+f'(a)(x-a)+{frac {f''(a)}{2!}}(x-a)^{2}+cdots +{frac {f^{(k)}(a)}{k!}}(x-a)^{k},}

is called the Taylor polynomial of order k of the function f at point a. The Taylor polynomial is the only polynomial that "best approximates the function asymptotically", in the sense that if there exists a function h_k: R → R and a polynomial p of order k such that

{displaystyle f(x)=p(x)+h_{k}(x)(x-a)^{k},quad lim _{xto a}h_{k}(x)=0,}

so p = P_k. Taylor's theorem describes the asymptotic behavior of the remainder term

{displaystyle R_{k}(x)=f(x)-P_{k}(x),}

which is the approximation error when approximating f with its Taylor polynomial. Using Taylor's notation or theorem, it can be expressed as follows:

{displaystyle R_{k}(x)=o(|x-a|^{k}),quad xto a.}

Explicit formulas for the rest

There are different ways of expressing ${displaystyle R_{k}(x)}$ mentioned below:

Average value form of the rest. Sea f: R → R, differential k+ 1 times in the open interval f^(k+1) continuous in the closed interval a and x. Then
(2nd) ${displaystyle R_{k}(x)={frac {f^{(k+1)}(xi _{L})}{(k+1)!}}(x-a)^{k+1}}$
for some real number roga_L between a and x. This is the shape of Lagrangethe rest. Similarly,
(2b) ${displaystyle R_{k}(x)={frac {f^{(k+1)}(xi _{C})}{k!}}(x-xi _{C})^{k}(x-a)}$
for some real number roga_C between a and x. This is the shape of Cauchythe rest.

Usually, this refinement of Taylor's theorem is proved with the mean value theorem, hence its name. Similar expressions can also be found. For example, if G(t) is continuous on the closed interval and differentiable with nonzero derivatives on the open interval between a and x, then

{displaystyle R_{k}(x)={frac {f^{(k+1)}(xi)}{k!}}(x-xi)^{k}{frac {G(x)-G(a)}{G'(xi)}}}

for some number ξ between a and x. This version generalizes the Lagrange and Cauchy forms of the remainder, which are taken as special cases, and are proved using Cauchy's mean value theorem.

In the case of the integral form of the remainder, concepts from Lebesgue integral theory are required for complete generality. However, the concept provided by the Riemann integral is maintained where the (k + 1)-th derivative of f is continuous on the closed interval [a ,x].

Integral form of the rest.Sea f^(k), continue absolutely in the closed interval a and x. Then
(3) ${displaystyle R_{k}(x)=int _{a}^{x}{frac {f^{(k+1)}(t)}{k!}}(x-t)^{k},dt.}$

Because of the absolute continuity of f ^(k) in the closed interval between a and x its derivative f ^(k+1) exists as a function L¹, and the result can be proved with a formal calculus using the Fundamental Theorem of Calculus and Integration by Parts.

For some functions $f(x)$ You can prove the rest, ${displaystyle R_{n}(f)}$ , approaches zero when $n$ approaching infinity; such functions can be expressed as Taylor series in a reduced environment around a point $a$ and are called analytical functions.

Taylor's theorem with ${displaystyle R_{n}(f)}$ expressed in the second form is also valid if the function $f$ has complex numbers or vector values. There is also a variation of Taylor's theorem for functions with multiple variables.

Dimension of the rest

It is often very useful in practice to embrace the term of the rest of Taylor's approach, rather than having the exact formula of this. Assuming that f It is continually differential ${displaystyle k+1}$ times in an interval $I$ containing a $a$ . We assume there are constants $q$ and $Q$ such as

{displaystyle qleq f^{(k+1)}(x)leq Q}

in the interval $I$ . Then the term of the rest satisfies inequality

{displaystyle q{frac {(x-a)^{k+1}}{(k+1)!}}leq R_{k}(x)leq Q{frac {(x-a)^{k+1}}{(k+1)!}}.}

Yeah. $a}" xmlns="http://www.w3.org/1998/Math/MathML">x▪a{displaystyle x PHPa}a}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1eee4914bb66c389a79d6ef84c4dcbffe5c122ab" style="vertical-align: -0.338ex; width:5.658ex; height:1.843ex;"/>$ and similarly if $<math alttext="{displaystyle x x.a{displaystyle x visa} <img alt="{displaystyle x$ . This is a simple consequence of the Lagrange form of the rest. In particular, if

{displaystyle |f^{(k+1)}(x)|leq M}

over an interval ${displaystyle I=(a-r,a+r)}$ with some $0}" xmlns="http://www.w3.org/1998/Math/MathML">r▪0{displaystyle rhab0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/23cbbcd53bd13620bc53490e3eec42790850b452" style="vertical-align: -0.338ex; width:5.31ex; height:2.176ex;"/>$ then.

{displaystyle |R_{k}(x)|leq M{frac {|x-a|^{k+1}}{(k+1)!}}leq M{frac {r^{k+1}}{(k+1)!}}}

for everything ${displaystyle xin (a-r,a+r)}$ . The second inequality is called uniform attachment, because it remains uniformly for everything x on the interval ${displaystyle (a-r,a+r)}$ .

Example

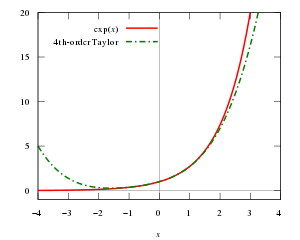
Approximation of e^x (blue) for his Taylor polynomial P_k of order k = 1,..., 7 focusing x= 0 (red)

Assuming you want to approximate the function f (x) = e^x in the interval [−1,1] with an error of no more than 10⁻⁵. This example requires the following properties of the exponential function to be known:

(♪) $0,qquad xin mathbb {R}.}" xmlns="http://www.w3.org/1998/Math/MathML">e0=1,ddxex=ex,ex▪0,x한 한 R.{displaystyle qquad e^{0}=1,qquad {frac {d}{dx}}}e^{x},qquad e^{x}{x}{x},qquad xin mathbb {R}. !0,qquad xin mathbb {R}.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f7b8842a591e888d3f468a3797a0f1a7f7a76b8f" style="vertical-align: -2.005ex; width:52.085ex; height:5.509ex;"/>$

Of these properties we have that f ^(k)( x) = e^x for all k, and in particular, f ^(k)(0) = 1. Then the Taylor polynomial of order k of f at 0 and its remainder in Lagrange form are:

{displaystyle P_{k}(x)=1+x+{frac {x^{2}}{2!}}+cdots +{frac {x^{k}}{k!}},qquad R_{k}(x)={frac {e^{xi }}{(k+1)!}}x^{k+1},}

where ξ is some number between 0 and x. Since e^x is increasing (*), we can simply use that e^x ≤ 1 for x ∈ [−1, 0] to bound the remainder over the subinterval [−1, 0]. To get an upper bound for the remainder on [0,1], we use the property e^ξ < e^x for 0<ξ<x to bound

<math alttext="{displaystyle e^{x}=1+x+{frac {e^{xi }}{2}}x^{2}<1+x+{frac {e^{x}}{2}}x^{2},qquad 0ex=1+x+eroga roga 2x2.1+x+ex2x2,0.x≤ ≤ 1{displaystyle e^{x}=1+x+{frac {e{xi}}{2}}x^{2}{2}{2}{2}{2}{2}{2}}{2}{2}{2}{2}{qquad 0ιxleq 1}<img alt="{displaystyle e^{x}=1+x+{frac {e^{xi }}{2}}x^{2}<1+x+{frac {e^{x}}{2}}x^{2},qquad 0

using the second-order Taylor expansion. Then we solve for e^x to deduce that

{displaystyle e^{x}leq {frac {1+x}{1-{frac {x^{2}}{2}}}}=2{frac {1+x}{2-x^{2}}}leq 4,qquad 0leq xleq 1}

simply by maximizing the numerator and minimizing the denominator. Combining these bounds for e^x we see that

{displaystyle |R_{k}(x)|leq {frac {4|x|^{k+1}}{(k+1)!}}leq {frac {4}{(k+1)!}},qquad -1leq xleq 1,}

this achieves the required precision, where

<math alttext="{displaystyle {frac {4}{(k+1)!}}<10^{-5}quad Longleftrightarrow quad 4cdot 10^{5}4(k+1)!.10− − 5 4⋅ ⋅ 105.(k+1)! k≥ ≥ 9.{displaystyle {frac {4}{(k+1)}}}}}}{quad Longleftrightarrow quad 4cdot 10^{5}{5}{quad Longleftrightarrow quad kgeq 9. !<img alt="{displaystyle {frac {4}{(k+1)!}}<10^{-5}quad Longleftrightarrow quad 4cdot 10^{5}

(see factorial or manually calculate the values 9!=362 880 and 10!=3 628 800). As a conclusion, Taylor's theorem allows the approximation

<math alttext="{displaystyle e^{x}=1+x+{frac {x^{2}}{2!}}+cdots +{frac {x^{9}}{9!}}+R_{9}(x),qquad |R_{9}(x)|ex=1+x+x22!+ +x99!+R9(x),日本語R9(x)日本語.10− − 5,− − 1≤ ≤ x≤ ≤ 1.{displaystyle e^{x}=1+x+{frac {x^{2}}{2}}}}+cdots +{frac {x^{9}{9}}}{9}}}+R_{9}(x),qquad ΔR_{9}(x){10^{-5},qquad -1leq xleq. !<img alt="{displaystyle e^{x}=1+x+{frac {x^{2}}{2!}}+cdots +{frac {x^{9}}{9!}}+R_{9}(x),qquad |R_{9}(x)|

This approximation then gives us the decimal expression e ≈ 2.71828, correct to five decimal places.

Demo

{displaystyle h_{k}(x)={begin{cases}{frac {f(x)-P(x)}{(x-a)^{k}}}&xnot =a\0&x=aend{cases}}}

where, as it says in the statement of Taylor's theorem,

{displaystyle P(x)=f(a)+f'(a)(x-a)+{frac {f''(a)}{2!}}(x-a)^{2}+cdots +{frac {f^{(k)}(a)}{k!}}(x-a)^{k}.}

It is enough to show that

{displaystyle lim _{xto a}h_{k}(x)=0.}

The demonstration of (1) is based on the repeated application of the L'Hôpital rule. It is observed that for each j = 0, 1,..., k−1, ${displaystyle f^{(j)}(a)=P^{(j)}(a)}$ . Hence each of the first k−1 derived from the numerator in ${displaystyle h_{k}(x)}$ is annulled ${displaystyle x=a}$ And the same happens to the denominator. Also, since the condition that the function f Whatever. k times differential at a point requires differentiability of order k−1 in an environment of that point (that is, because differentiability requires a function defined in a point environment), the numerator and its k− 2 derivatives are differential in an environment of a. Clearly, the denominator also satisfies that condition, and additionally, it is not nullified unless x=a, therefore all the conditions for the rule of L'Hopital are met, and thus its use is justified. So.

{displaystyle {begin{aligned}lim _{xto a}{frac {f(x)-P(x)}{(x-a)^{k}}}&=lim _{xto a}{frac {{frac {d}{dx}}(f(x)-P(x))}{{frac {d}{dx}}(x-a)^{k}}}=cdots =lim _{xto a}{frac {{frac {d^{k-1}}{dx^{k-1}}}(f(x)-P(x))}{{frac {d^{k-1}}{dx^{k-1}}}(x-a)^{k}}}\&={frac {1}{k!}}lim _{xto a}{frac {f^{(k-1)}(x)-P^{(k-1)}(x)}{x-a}}\&={frac {1}{k!}}(f^{(k)}(a)-f^{(k)}(a))=0end{aligned}}}

where the penultimate equality remains by the definition of the derivative in x = a.

Getting the mean form of the remainder

Let G be a real function, continuous over a closed interval between a and x and differentiable with nonzero derivatives over the open interval between a and x, and the function that is defined as

{displaystyle F(t)=f(t)+f'(t)(x-t)+{frac {f''(t)}{2!}}(x-t)^{2}+cdots +{frac {f^{(k)}(t)}{k!}}(x-t)^{k}.}

Then, by Cauchy's mean value theorem,

{displaystyle (*)quad {frac {F'(xi)}{G'(xi)}}={frac {F(x)-F(a)}{G(x)-G(a)}}}

for some ξ over the open interval between a and x. We note that the numerator F(x) − F(a) = R_k(x) is exactly the remainder of the Taylor polynomial for f(x). Calculated

{displaystyle {begin{aligned}F'(t)={}&f'(t)+{big (}f''(t)(x-t)-f'(t){big)}+left({frac {f^{(3)}(t)}{2!}}(x-t)^{2}-{frac {f^{(2)}(t)}{1!}}(x-t)right)+cdots \&cdots +left({frac {f^{(k+1)}(t)}{k!}}(x-t)^{k}-{frac {f^{(k)}(t)}{(k-1)!}}(x-t)^{k-1}right)={frac {f^{(k+1)}(t)}{k!}}(x-t)^{k},end{aligned}}}

substituting into (*) and rearranging the terms to find that

{displaystyle R_{k}(x)={frac {f^{(k+1)}(xi)}{k!}}(x-xi)^{k}{frac {G(x)-G(a)}{G'(xi)}}.}

This is the form of the term we mentioned as "remain", then we set Taylor's theorem with the rest in the form of the average value. The Lagrange shape of the rest can be obtained by doing ${displaystyle G(t)=(t-x)^{k+1}}$ and the form of Cauchy doing ${displaystyle G(t)=t-a}$ .

Observation. Using this method you can also resort to the integral form of the remainder by doing

{displaystyle G(t)=int _{a}^{t}{frac {f^{(k+1)}(s)}{k!}}(x-s)^{k},ds,}

but the requirements of f needed to use the mean value theorem are stronger, if one has the goal of proving the case where f ^(k) is only absolutely continuous. However, if the Riemann integral is used instead of the Lebesgue integral, the requirements cannot be so weak.

Obtaining the integral form of the remainder

Because of the absolute continuity of f ^(k) over the closed interval between a and x its derivative f ^(k+1) exists as a function L¹, and the fundamental theorem of calculus and integration by parts is used. This same proof is applied for the Riemann integral, taking into account that f ^(k) is continuous on the closed interval and differentiable on the interval open between a and x, and this leads to the same result as when using the mean value theorem.

The fundamental theorem of calculus says that

{displaystyle f(x)=f(a)+int _{a}^{x},f'(t),dt.}

From here integration by parts is used and once more the Fundamental Theorem of Calculus is used to see that

{displaystyle {begin{aligned}f(x)&=f(a)+{Big (}xf'(x)-af'(a){Big)}-int _{a}^{x}tf''(t),dt\&=f(a)+xleft(f'(a)+int _{a}^{x}f''(t),dtright)-af'(a)-int _{a}^{x}tf''(t),dt\&=f(a)+(x-a)f'(a)+int _{a}^{x},(x-t)f''(t),dt,end{aligned}}}

which is exactly Taylor's theorem with remainder in integral form for the case k=1. The general statement is proved using induction. Supposing that

{displaystyle (*)quad f(x)=f(a)+{frac {f'(a)}{1!}}(x-a)+cdots +{frac {f^{(k)}(a)}{k!}}(x-a)^{k}+int _{a}^{x}{frac {f^{(k+1)}(t)}{k!}}(x-t)^{k},dt.}

Integrating the remainder term by parts, we get that

{displaystyle {begin{aligned}int _{a}^{x}{frac {f^{(k+1)}(t)}{k!}}(x-t)^{k},dt=&-left[{frac {f^{(k+1)}(t)}{(k+1)k!}}(x-t)^{k+1}right]_{a}^{x}+int _{a}^{x}{frac {f^{(k+2)}(t)}{(k+1)k!}}(x-t)^{k+1},dt\=& {frac {f^{(k+1)}(a)}{(k+1)!}}(x-a)^{k+1}+int _{a}^{x}{frac {f^{(k+2)}(t)}{(k+1)!}}(x-t)^{k+1},dt.end{aligned}}}

Substituting this into the formula in (*) shows that if it holds for the value k, it should also hold for the value k + 1. Therefore, since we have for k = 1, we have for any positive integer value k.

Case of several variables

The theorem of Taylor above (1) can be generalized to the case of several variables as explained below. Sea B a ball in $mathbb {R} ^{n}$ centered aand f a defined real function on the closing ${displaystyle {bar {B}}}$ whose partial derivatives to order n+1 are all continuous at each point of the ball. Taylor's theorem states that for any ${displaystyle xin B}$ :

${displaystyle f(x)=sum _{|alpha |=0}^{n}{frac {1}{alpha !}}{frac {partial ^{alpha }f(a)}{partial x^{alpha }}}(x-a)^{alpha }+sum _{|alpha |=n+1}R_{alpha }(x)(x-a)^{alpha }}$ ,

where the sum is spread over the multi-indices α (this formula uses the multi-index notation). The remainder satisfies the inequality:

${displaystyle |R_{alpha }(x)|leq sup _{yin {bar {B}}}left|{frac {1}{alpha !}}{frac {partial ^{alpha }f(y)}{partial x^{alpha }}}right|}$

for all α with |α|=n+1. As in the case of one variable, the remainder can be expressed explicitly in terms of higher derivatives (see the proof for details).

Demo

To demonstrate Taylor's theorem for the multidimensional case, consider a function ${displaystyle f:mathbb {R} ^{n}to mathbb {R} }$ or climbing field, we assume continuous and, to simplify the exposed (although a generalization is trivial), class ${displaystyle C^{infty }}$ . Sea ${displaystyle mathbf {r} (t)}$ a vector function ${displaystyle mathbb {R} to mathbb {R} ^{n}}$ and define it as ${displaystyle mathbf {r} (t)=mathbf {a} +mathbf {u} t}$ (from now on, the arrows of the vectors will be omitted). Let's go. ${displaystyle mathbf {r} (t)=mathbf {y} }$ Now let's do it. ${displaystyle g(t)=f[mathbf {r} (t)]}$ and remember that ${displaystyle g^{prime }(t)=nabla f(mathbf {y})mathbf {r} ^{prime }(t)}$ . Let's note now that:

${displaystyle g^{prime prime }(t)=u_{1}[D_{11}f(mathbf {y})u_{1}+..+D_{1n}f(mathbf {y})u_{n}]+ldots +u_{n}[D_{n1}f(mathbf {y})u_{1}+..+D_{nn}f(mathbf {y})u_{n}]=sum _{j=1}^{n}sum _{i=1}^{n}{dfrac {partial ^{2}f(mathbf {y})}{partial x_{j}partial x_{i}}}u_{j}u_{i}}$

Now, deriving successive times, we find that we can put in a very comfortable way:

${displaystyle g^{(n)}(t)=(mathbf {u} cdot nabla)^{n}f(mathbf {y})}$

where the vector scale product $mathbf{u}$ with the gradient ${displaystyle nabla }$

${displaystyle mathbf {u} cdot nabla =u_{1}partial _{1}+cdots +u_{n}partial _{n}}$

represents the directional derivative, and the exponent $n$ about it is understood as the successive times we do it on the function; that is, we do the directional derivative $n$ Sometimes. Now, using Taylor's theorem for a real variable, we expand ${displaystyle g(t)}$ in his McLaurin series:

${displaystyle g(t)=g(0)+g^{prime }(0)t+{dfrac {g^{prime prime }(0)}{2!}}t^{2}ldots =sum _{k=0}^{infty }{dfrac {g^{(k)}(0)}{k!}}t^{k}}$

and making t=1 and substituting the derivatives for the expressions found before, it is evident that:

${displaystyle f(mathbf {a} +mathbf {u})=f(mathbf {a})+(mathbf {u} cdot nabla)f(mathbf {a})+{dfrac {(mathbf {u} cdot nabla)^{2}f(mathbf {a})}{2!}}+dots =sum _{k=0}^{infty }{dfrac {(mathbf {u} cdot nabla)^{k}f(mathbf {a})}{k!}}}$

Note that the first term appears the gradient and the second the Hessian matrix, but written with this particular notation that is more comfortable and compact. The expression obtained is equivalent to the one expressed above using the multi-index notation.

Contenido relacionado

Más resultados...

Taylor's theorem

Instance of a variable

Statement of the theorem

Explicit formulas for the rest

Dimension of the rest

Example

Demo

Getting the mean form of the remainder

Obtaining the integral form of the remainder

Case of several variables

Demo

Contenido relacionado

Variance

System reliability

Rudolf Lipschitz