Surface (topology)

_ㅤFor more extensive coverage of this topic, see : Surface (mathematics)

An open surface with the contours x{displaystyle x}, and{displaystyle and} and z{displaystyle z} shown.

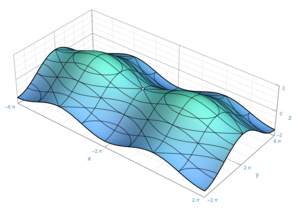
In the part of mathematics called topology, a surface is a two-dimensional manifold. Some surfaces emerge as boundaries of three-dimensional solids; for example, the sphere is the limit of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure on the right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

Topological surfaces are sometimes endowed with additional information, such as a Riemann metric or a complex structure, which connects them to other mathematical disciplines, such as differential geometry and complex analysis. The various mathematical notions of surface can be used to model surfaces in the physical world.

Generally

In mathematics, a surface is a geometric shape that resembles a deformed plane. The best known examples arise as limits of solid objects in ordinary Euclidean space R³, such as spheres. The exact definition of a surface may depend on the context. Normally, in algebraic geometry, a surface can intersect itself (and can have other singularities), whereas it cannot in topology and differential geometry.

Properties and types of surfaces

Usual surfaces are curved versions of the plane, in fact they are locally homeomorphic to it. Therefore, it is not strange that several types of interesting surfaces in applications are defined from curvature properties with respect to the Euclidean plane or in terms of isometries. In addition, other interesting topological concepts such as orientability allow to formally express certain properties of surfaces.

Closed surfaces

An example of a surface closed and multiplely connected is the triple bull.

Intuitively, a closed surface in three-dimensional space is any surface that encloses a volume, dividing said space into a "bounded" and an "unbounded" region. In 4 or more dimensions there are also closed surfaces but the previous intuitive notion is not valid, since closed surfaces in more dimensions do not divide space in this way.

• It can be verified that in three dimensions a surface without edge encloses a volume, such as the sphere and the bull or "donut", these surfaces are also orientable surfaces. In fact all closed surfaces immersed in the three-dimensional space are oriented, unlike what happens in more dimensions.
• Other more exotic closed surfaces are the projective plane and Klein bottle (definable in 4 dimensions).
• A disc (in R2{displaystyle mathbb {R} ^{2}}), a finite cylinder or the Möbius band are examples of border surfaces. Like the image on the right.

Developable, ruled and warped surfaces

Some surfaces have interesting properties that are expressible in terms of their curvature, these types are developable, ruled and warped surfaces:

• Intuitively a surface is undeveloped if it can be manufactured from an euclide plane by "folding". The cone and the cylinder are undeveloped, which shows that appropriate models can be built from a sheet of paper or flat cardboard. Formally given developmental surface There is an isometry between the surface and the euclid plane. A necessary and sufficient condition for a surface to develop, stems from theorema egregium de Gauss, is that the Gaussian curvature of this surface is identically null.
• One surface is regulated when the tangent plane for each point of the same contains a straight line completely contained on the surface. A necessary condition is that the second fundamental form is at that point an indefinite quadratic form and therefore the Gaussian curvature is negative.
• One flat surface is a regulated and undeveloped surface.

Adjustable surfaces

The Möbius band is a non-orientated surface with a border (its border is a simple closed curve).

A last less intuitive property is that of orientability, which allows us to distinguish between orientable and non-orientable surfaces. An orientable surface can be defined simply as an orientable manifold of dimension two, where every contained simple closed curve has a regular homeomorphic neighborhood to an open cylinder. Any two-dimensional manifold that is not orientable is a non-orientable surface. That is, there exists at least one contained simple closed curve that has a regular neighborhood homeomorphic to a Möbius band.

The closed orientable surfaces have the property of dividing three-dimensional space (where they can always be embedded) into two different and disjoint regions: one bounded by said surface that is of finite volume and the other not bounded outside that volume.

This term is used to distinguish them from surfaces that do not contain anything inside, such as an infinite plane in reference to three-dimensional space. It is impossible to talk about non-orientable surfaces dividing three-dimensional space, since these surfaces cannot be embedded in it.

Closed Surface Classification Theorem

An important mathematical result is the closed surface classification theorem, which asserts that every closed surface (that is, compact and without a boundary or edge) is homeomorphic to any member of the following three surface families:

1. the field;
2. the related amount g{displaystyle g,}-Thurs, being g≥ ≥ 1{displaystyle ggeq 1};
3. the related amount k actual plans, being k≥ ≥ 1{displaystyle kgeq 1}.

In other words, the above surfaces are all the closed surfaces that exist (except homeomorphism). The surfaces of the first two families are orientable. It is convenient to combine the first two families, considering the sphere as the related sum of zero bulls. Number g of bulls involved in the construction is called surface gender. Since the sphere and bull have characteristics of Euler 2 and 0, respectively, it is deduced that the characteristic of Euler of the related sum of g Bulls is precisely 2− − 2g{displaystyle 2-2g,}.

Deforming a 2- Variety border.

The surfaces of the third family are non-oriented. The characteristic of Euler of the real projective plane is 1, thus the related sum k of them is 2− − k{displaystyle 2-k,}.

From all this it follows that a closed surface is determined -except for homeomorphism- by two properties: the numerical value of its Euler characteristic (or its genus) and whether or not it is orientable.

It is also possible to classify surfaces that are not closed (that is, with a boundary). This is obtained as the previous scheme, adding the number of borders that the surface has.