Surface tension
The surface tension of a liquid is the amount of energy required to increase its surface area per unit area. This definition implies that the liquid exhibits resistance as its surface area increases, which in effect It allows some insects to be able to move on the surface of the water without sinking. Surface tension is a manifestation of intermolecular forces in liquids, together with the forces that occur between liquids and solid surfaces that come into contact with them, giving rise to capillarity. The effect is the elevation or depression of the surface of a liquid in the area of contact with a solid.
Another possible definition of surface tension: it is the force that acts tangentially per unit length on the edge of a free surface of a liquid in equilibrium and that tends to contract said surface. The cohesive forces between the molecules of a liquid are responsible for the phenomenon known as surface tension.
Cause
Surface tension is due to the fact that the forces that affect each molecule are different inside the liquid and on the surface. Thus, within a liquid, each molecule is subjected to attractive forces that cancel each other out on average. This allows the molecule to have a fairly low energy. However, at the surface there is a net force toward the interior of the liquid. Strictly speaking, if there is a gas on the outside of the liquid, there will be a minimal attractive force towards the outside, although in reality this force is negligible due to the great difference in densities between the liquid and gas.
Another way of looking at it is that a molecule in contact with its neighbor is in a lower energy state than if it were not in contact with that neighbor. The inner molecules have all the neighboring molecules they could have, but the outer particles have fewer neighboring particles than the inner ones and so have a higher energy state. For the liquid, to lower its energy state is to minimize the number of particles on its surface.
Energetically, the molecules located on the surface have a higher average energy than those located inside, therefore the tendency of the system will be to decrease the total energy, and this is achieved by decreasing the number of molecules located on the surface, hence the area reduction to the minimum possible.
As a result of minimizing the surface, it will assume the smoothest shape it can since it is mathematically proven that surfaces minimize area by the Euler-Lagrange equation. In this way the liquid will try to reduce any curvature on its surface to decrease its energy state in the same way that a ball falls to the ground to decrease its gravitational potential.
Symbols
| Symbol | Name | Unit |
|---|---|---|
| γ γ {displaystyle gamma } | Surface tension | mN / m |
| Surface area growth | ||
| F{displaystyle F} | Force | |
| L{displaystyle L} | Length | |
| Floating objects | ||
| Fs{displaystyle F_{s}} | Surface strength | |
| Fw{displaystyle F_{w}} | Weight strength | |
| g{displaystyle g} | Acceleration of gravity | |
| m{displaystyle m} | Masa | |
| Surface healing and pressure | ||
| Δ Δ p{displaystyle Delta p} | Pressure Difference (Laplace Pressure) | N/m2 |
| Rx{displaystyle R_{x}} | Curve radio on the x-axis | |
| Rand{displaystyle R_{y} | Curve radio in the axis and | |
| Vertical tube liquid | ||
| γ γ la{displaystyle gamma _{la}} | Surface tension between liquid and air | mN / m |
| ρ ρ {displaystyle rho } | Density | kg / m3 |
| h{displaystyle h} | Altitude of fluid that is lifted | |
| r{displaystyle r} | Radio de capilaridad | |
| θ θ {displaystyle theta } | Contact angle | |
| Charges on a surface | ||
| hp{displaystyle h_{p}} | Depth of puddle | |
| Thermodynamic theories of surface tension | ||
| μ μ i{displaystyle mu _{i}} | Chemical potential | |
| Ω Ω {displaystyle Omega } | Free energy | N m |
| Ω Ω s{displaystyle Omega _{s}} | Surface-free energy | N m |
| Δ Δ P{displaystyle Delta P} | Pressure variance | N/m2 |
| pA{displaystyle p_{A}} | Inner pressure | N/m2 |
| pB{displaystyle p_{B}} | External pressure | N/m2 |
| T{displaystyle T} | Temperature | K |
| V{displaystyle V} | Molar volume of the substance | |
| Thermodynamic Bubbles | ||
| A{displaystyle A} | Area | m2 |
| R{displaystyle R} | Radio | m |
| Temperature Influence | ||
| γ γ or{displaystyle gamma ^{o}} | Constant surface tension for each substance | mN / m |
| K2{displaystyle K_{2}} | Universal Constant for Liquids | |
| k{displaystyle k} | Constant validated for almost any substance | |
| n{displaystyle n} | Empirical factor | |
| Pc{displaystyle P_{c}} | Critical pressure | N/m2 |
| Tc{displaystyle T_{c}} | Critical temperature | K |
| Influence by Concentration of solute | ||
| Interpreter Interpreter {displaystyle Gamma } | Surface concentration | mol / m2 |
| C{displaystyle C} | Concentration of the substance | |
| Influence by particle size in steam pressure | ||
| PVor{displaystyle P_{V}{o}{o}} | Standard steam pressure | N/m2 |
| R{displaystyle R} | Constant gas | |
| rk{displaystyle r_{k}} | Radio Kelviin | |
| Water | ||
| γ γ w{displaystyle gamma _{w}} | Surface water tension | mN / m |
| γ γ ws{displaystyle gamma _{ws}} | Surface saltwater tension | mN / m |
| S{displaystyle S} | Baseline balance | g/kg |
| t{displaystyle t} | Temperature | °C |
Properties
Some properties of γ γ {displaystyle scriptstyle gamma }:
- γ γ {displaystyle scriptstyle gamma } 0, since to increase the state of the liquid in contact it is necessary to carry more molecules to the surface, thereby reducing the energy of the system and γ γ {displaystyle scriptstyle gamma } That's it.
- or the amount of work necessary to carry a molecule to the surface.
- γ γ {displaystyle scriptstyle gamma } depends on the nature of the two phases in contact which, in general, will be a liquid and a solid. Thus, the surface tension will be equal for example for water in contact with its steam, water in contact with an inert gas or water in contact with a solid, to which it may wet or not (see capillary) due to the differences between the cohesive forces (within the liquid) and the adhesives (liquid-superficie).
- γ γ {displaystyle scriptstyle gamma } can be interpreted as a force per unit length (measured in N·m−1). This can be illustrated by considering a biphasic system controlled by a mobile piston, in particular two liquids with different surface tension, such as water and hexan. In this case the liquid with greater surface tension (water) will tend to decrease its surface at the expense of increasing the hexan, of less surface tension, which translates into a net force that moves the piston from the hexan to the water.
- The value of γ γ {displaystyle scriptstyle gamma } depends on the magnitude of intermolecular forces within the liquid. Thus, the greater the forces of fluid cohesion, the greater the superficial tension. We can illustrate this example by considering three liquids: hexan, water and mercury. In the case of the hexan, intermolecule forces are Van der Waals forces. The water, apart from that of Van der Waals, has hydrogen bridge interactions, of greater intensity, and the mercury is subject to the metallic link, the most intense of the three. So, the γ γ {displaystyle scriptstyle gamma } from each liquid grows from hexan to mercury.
- For a given liquid, the value of γ γ {displaystyle scriptstyle gamma } decreases with temperature, due to the increase in thermal agitation, resulting in a lower effective intensity of intermolecule forces. The value of γ γ {displaystyle scriptstyle gamma } tends to zero as temperature approaches critical temperature Tc of the compound. At this point, the liquid is indistinguishable from the steam, forming a continuous phase where there is no defined surface between both, disappearing the two phases. With only one phase, the surface tension is 0.
Surface tension effects
Water
Various effects of surface tension can be seen with ordinary water.
- Rainwater accounts on a zero surface, such as leaves. The water is weakly attached to the wax and strongly attached to itself, so the water is clustered in drops. Surface tension gives them their almost spherical form, since a sphere has the smallest possible reason of surface area to volume.
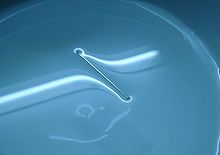
- The formation of drops occurs when a fluid mass is elongated. The animation below shows water adhering to the water valve gaining mass until it is lengthened to a point where the surface tension can no longer hold the drop linked to the water valve. Then it separates and the surface tension forms the drop in a sphere. If a water jet runs through the water valve, the jet would break in drops during its fall. Gravity lengthens the jet, then the superficial tension pinches it in spheres.
- Floating more dense objects than water occurs when the object is non-modable and its weight is small enough to be transported by forces raised by surface tension. For example, skater chinches use surface tension to walk over the pond surface as follows. The ability not to get wet from the legs of the skater chinches means that there is no attraction between the paw molecules and the water molecules, so when the paw pushes down on the water, the surface water tension only tries to recover its planity from its deformation due to the paw. This water behavior pushes the skating chinche upwards, so you can stop on the water surface as much as your mass is small enough that the water can support it. The surface of the water behaves like an elastic film: the leg of the insect causes cracks on the surface of the water, increasing its surface area and tendency to minimize superficial curvature (as well as area) of the water pushes the leg of the insect upwards.
- Separation of oil and water (in this case, water and liquid wax) is caused by a surface tension between different liquids. This type of surface tension is called "interfacial pressure", but its chemistry is the same.
- The tears of wine is the formation of drops and streams on the side of the glass containing an alcoholic drink. Its cause is a complex interaction between the different surface water and ethanol tensions, it is induced by a combination of surface water pressure modification by ethanol along with faster ethanol evaporation than water.
Surfactants
Surface tension is visible in another common phenomenon, especially when surfactants are used to reduce it.
- Soap bubbles have very large surface area with very little mass. The bubbles in pure water are unstable. The addition of surfactants, however, may have a stabilizing effect on the bubbles (see Effect Marangoni). Note that surfactants actually reduce surface water tension by a factor of three or more.
- Emulsions are a type of colloid in which surface tension plays a role. Small pieces of oil suspended in pure water will be spontaneously assembled in much larger masses. But, the presence of a surfactant provides a decrease in surface tension, which allows the stability of tiny drops of oil in the whole of the water (or vice versa).
Physics
Physical units
The surface tension, represented by the symbol (γ γ {displaystyle gamma }), alternatively (σ σ {displaystyle sigma }or (T{displaystyle T}), is measured by force per unit length. Your SI unit is Newton per metre, but also used the cgs dyna unit per centimeter, for example,
γ γ =1dcm=1ergcm2=110− − 7m N10− − 4m2=0.001Nm=0.001Jm2{displaystyle gamma =1{text{text{dina}}{text{cm}{text}{text}{text{erg}}{{{{text}{text}{2}}}{1}{frac}{{frac}{}{text}{c}{ctext}{ctext}{c}{c}{f}{f}{f}{f}{f}{f}{f}{f}{f}{cd}{f}{cd}{cd}{cd}{cd}{f}{cd}{cd}{cd}{cd}{f}{cd}{cd}{f}{cd}{cd}{cd}{cd}{cd}{cd}{cd}{cd}{cd}}{c
Surface Area Growth
Surface tension can be defined in terms of force or energy.
In terms of strength
The surface tension (γ γ {displaystyle gamma }) of a liquid is the strength per unit length. In the illustration of the right, the rectangular picture, composed of three unmovable sides (black) that form a form of "U", and the fourth moving side (blue) that can slide to the right. The surface tension will flatten the blue bar to the left, the force (F{displaystyle F}) required to hold the moving side is proportional to length (L{displaystyle L}) on the unmovable side. So the reason (FL{displaystyle {frac {F}{L}}}}) depends only on the intrinsic properties of the liquid (composition, temperature, etc.), not on its geometry. For example, if the picture had a more complicated form, the reason (FL{displaystyle {frac {F}{L}}}}), with (L{displaystyle L}) length of the moving side and force (F{displaystyle F}) required to stop it from slipping, it is found to be the same for all forms. So, we define the surface tension as:
γ γ =F2L{displaystyle gamma ={frac {F}{2L}}}}}.
The reason for the 1/2 is that the film has two sides (two surfaces), each of which contributes equally in force, so the force contributed for only one side is:
γ γ L=F2{displaystyle gamma l={frac {F}{2}}}}}
In terms of energy
The surface tension (γ γ {displaystyle gamma }) of a liquid is the reason for change in the energy of the liquid to change in the surface area of the liquid (this leads to the change of energy). This can be easily related to the previous definition in terms of force. Yeah.F{displaystyle F}) is the force required to stop the side of starting to slide, then this is also the force that will keep the side in the slip state at a constant speed (by the Second Law of Newton). But, if the side moves to the right (in the direction in which the force is applied), then the surface area of the elongated fluid is increasing while the applied force exerts work in the liquid. This means that increasing the surface area increases the energy of the film. The work done by force (F{displaystyle F}) to move the side for a distance (Δ Δ x{displaystyle Delta x}) is (W=FΔ Δ x{displaystyle W=FDelta x}), at the same time the total area of the film is increased by (Δ Δ A=2LΔ Δ x{displaystyle Delta A=2LDelta x}) (the factor of 2 is here as the liquid has two sides, two surfaces). Thus, multiplying both, numerator and denominator (γ γ =F2L{displaystyle gamma ={frac {F}{2L}}}}}) by (Δ Δ x{displaystyle Delta x}), we have:
γ γ =F2L=F2LΔ Δ xΔ Δ x=WΔ Δ A{displaystyle gamma ={frac {F}{2L}}}={frac {F}{2L}}}}{frac {Delta x}{Delta x}}}}{frac {W}{Delta A}}}}}}.
This work is, by the usual arguments, interpreted as being stored as potential energy. Consequently, surface tension can also be measured in the SI System as J / m2 and in the cgs System as erg / cm2. Since mechanical systems try to find a state of minimum potential energy, a free drop of liquid naturally assumes a spherical shape, which has the minimum surface area for a given volume. The equivalence of measuring energy per unit area to force per unit length can be proven by dimensional analysis.
Surface curvature and pressure
If no force acts normal to a stressed surface, the surface must remain flat. But, if a pressure on one side of the surface differs from the pressure on the other side, the difference in pressure times the surface area results in a normal force. In order for the forces of surface tension to cancel the force due to pressure, the surface must curve. The diagram shows how the surface of curvature of a small surface patch guides a net component of surface tension forces acting normal to the center of the patch. When all the forces are balanced, the resulting equation is known as the Young-Laplace Equation:
Δ Δ p=γ γ (1Rx+1Rand){displaystyle Delta p=gamma {Bigl (}{frac {1}{R_{x}}}}}}{frac {1}{R_{y}}}}{Bigr)}}}}
The amount in parentheses on the right hand is actually (double) the mean curvature of the surface (depending on normalization). Solutions to this equation determine the shape of water droplets, puddles, menisci, soap bubbles, and all other shapes determined by surface tension (such as the surface of Gerridae paw prints on the surface of the surface). of a pond). The table below shows how the internal pressure of a drop of water increases with decreasing radius. For not very small droplets the effect is subtle, but the pressure difference becomes enormous as the droplet size approaches molecular size. (In the limit of a simple molecule the concept becomes meaningless.)
| Gout radio | 1 mm | 0.1 mm | 1 μm | 10 nm |
|---|---|---|---|---|
| Δ Δ p{displaystyle Delta p} (atm) | 0.0014 | 0.0144 | 1.436 | 143.6 |
Floating objects
When an object is placed in a liquid, its weight (Fw{displaystyle F_{w}}) depresses the surface, and if its surface tension and force down become equal, then they are balanced by the surface tension on each side (Fs{displaystyle F_{s}}), which are each parallel to the surface of the water at the points where it makes contact with the object. Note that a small movement in the body must cause the object to sink. As the contact angle decreases, the surface tension decreases. The horizontal component of the two arrows (Fs{displaystyle F_{s}}) point in opposite directions, so they cancel one to the other, but the vertical component points in the same direction and therefore add to balance (Fw{displaystyle F_{w}}). The surface of the object should not be wet for this to happen, and its weight must be low enough for the surface tension to support it. Yeah.m{displaystyle m}) denotes the needle mass and (g{displaystyle g}) the acceleration of gravity, we have:
| 1 | 2 | 3 | |
|---|---|---|---|
| Formula | Fw=2Fswithout θ θ {displaystyle F_{w}=2F_{s}sin theta } | Fw=mg{displaystyle F_{w}=mg} | Fs=γ γ L{displaystyle F_{s}=gamma L} |
| Replacement | mg=2γ γ Lwithout θ θ {displaystyle mg=2gamma Lsin theta } | ||
Liquid surface
To find the shape of the smallest surface bounded by some form of arbitrary frame using strictly mathematical means can be a daunting task. Even by modeling the framework out of wires and immersing it in a soap solution, a local minimal surface will appear on the resulting soap film in seconds.
The reason for this is that the pressure difference across a fluid interface is proportional to the mean curvature, as seen in the Young-Laplace equation. For an open soap film, the pressure difference is zero, so the mean curvature is zero, and minimal surfaces have the property of zero mean curvature.
Contact Angles
Main article: Contact angle
The surface of any liquid is an interface between that liquid and some other medium. The upper surface of a pond, for example, is an interface between the pond water and the air. Surface tension, then, is not a property of the liquid alone, but a property of the interface of the liquid with another medium. If the liquid is in a container, then, along with the liquid/air interface on its upper surface, there is also an interface between the liquid and the walls of the container. The surface tension between the liquid and air is usually different (greater) than the surface tension with the container walls. And where the two surfaces meet, their geometry must be such that all forces are balanced.
Where the two surfaces are found, they form a contact angle, which is the angle that the tangent to the surface makes with the solid surface. Note that the angle is measured through the liquid, as shown in the diagram above. The diagram on the right shows the two examples. Tension forces are shown for liquid interfase - air, liquid interface - solid, and solid interface - air. The example on the left is where the difference of the surface tension between the liquid - solid and solid - air, (γ γ ls− − γ γ sa{displaystyle gamma _{ls}-gamma _{sa}}) is less than the surface fluid tension - air (γ γ la{displaystyle gamma _{la}}) but it is despite that positive, this is:
gamma _{ls}-gamma _{sa}>0}" xmlns="http://www.w3.org/1998/Math/MathML">γ γ la▪γ γ ls− − γ γ sa▪0{displaystyle gamma _{la}schoolgamma _{ls}-gamma _{sa}gamma _{ls}-gamma _{sa}>0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e22560de4faa791630b99eb72cc960aaebf3c251" style="vertical-align: -0.838ex; width:18.771ex; height:2.676ex;"/>
In the diagram, both the vertical and horizontal force must be canceled exactly at the point of contact, known as balance. The horizontal component of (fla{displaystyle f_{la}) is canceled by adhesive force (fA{displaystyle f_{A}})
fA=flawithout θ θ {displaystyle f_{A}=f_{la}sin theta }
The most so-called force balance, though, is in the vertical direction. The vertical component of (fla{displaystyle f_{la}) must cancel the exact difference of forces along the surface of the solid (fls− − fsa{displaystyle f_{ls}-f_{sa}}}).
fls− − fsa=flawithout θ θ {displaystyle f_{ls}-f_{sa}=f_{la}sin theta }
This means that although the difference between surface fluid tension - solid and solid - air, (γ γ ls− − γ γ sa{displaystyle gamma _{ls}-gamma _{sa}}) is difficult to measure directly, can be inferred from the surface fluid tension - air (γ γ la{displaystyle gamma _{la}}) and the contact angle of balance (θ θ {displaystyle theta }), which is a function of the easy to measure, advance and backward contact angles (see the main article contact angle).
The same relationship exists in the diagram to the right. But in this case, we see that since the contact angle is less than 90°, the difference in surface tension of the liquid - solid / solid - air must be negative:
0>gamma _{ls}-gamma _{sa}}" xmlns="http://www.w3.org/1998/Math/MathML">γ γ la▪0▪γ γ ls− − γ γ sa{displaystyle gamma _{la}{la} verbal0 supposedgamma _{ls}-gamma _{sa}}}0>gamma _{ls}-gamma _{sa}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3f732ceb19c916ba089c20051b7101bfd785a9ba" style="vertical-align: -0.838ex; width:18.771ex; height:2.676ex;"/> θ θ {displaystyle theta } = 180°
| Liquid | Solid | Contact angle |
|---|---|---|
| Water | Lime soda glass
Lead glass Cast Quartz | 0° |
| Etanol | ||
| Dietil éter | ||
| Carbon tetrachloride | ||
| Glicerol | ||
| Acetic acid | ||
| Water | Paraffin wax | 107° |
| Silver | 90° | |
| Methyl iodide | Lime soda glass | 29° |
| Lead glass | 30° | |
| Cast Quartz | 33° | |
| Mercury | Lime soda glass | 140° |
Special contact angles
Note that in the special case of the water-silver interface, where the contact angle is equal to 90°, the difference between the liquid-solid / solid-air surface tension is exactly zero.
Another special case is where the contact angle is exactly 180°. Specially prepared Teflon water comes close to this. The 180° contact angle occurs when the liquid-solid surface tension is exactly equal to the liquid-air surface tension.
0}" xmlns="http://www.w3.org/1998/Math/MathML">γ γ la=γ γ ls− − γ γ sa▪0{displaystyle gamma _{la}=gamma _{ls}-gamma _{sa}{s”0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d4f59ed9c2bbb32f5d3c66f1249dd5af8f6f558c" style="vertical-align: -0.838ex; width:18.771ex; height:2.676ex;"/>
Measuring methods
Since surface tension manifests itself in various effects, it offers a number of ways to measure it. Which method is optimal depends on the nature of the liquid to be measured, the conditions under which its stress is to be measured, and the stability of its surface when deformed. An instrument that measures surface tension is called a tensiometer.
- Noüy Ring Method: The traditional method used to measure surface and interfacial tension. Wet properties of the surface or interface have little influence on this measurement technique. The maximum hale exercised in the ring by a surface is measured.
- Wilhelmy saucer method: A universal method specifically suited to verify surface tension over long time intervals. A vertical plate called perimeter is attached to a scale, and the strength due to the wet is measured.
- Rotating Drop Method: This technique is ideal for measuring low interfacial tensions. The diameter of the drop between a heavy phase is measured while both are rotating.
- Pendant gout method: Surface and interfacial tensions can be measured by this technique, even at high temperatures and pressures. The geometry of a drop is optically analyzed. For hanging drops the maximum diameter and the reason between these parameters and the diameter at the distance of the maximum diameter of the drop apex have been used to evaluate the measurement and shape parameters in order to determine the surface tension.
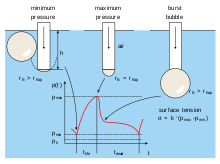
- Bubble Pressure Method (Jaeger Method): A measurement technique to determine surface tension at short surface ages. Maximum pressure for each bubble is measured.
- Drop volume method: A method to determine interfacial tension as an interfacial age function. A density liquid is pumped into a second fluid of different density and the time between drops produces is measurement.
- Capilar Lift Method: The end of a capillary is submerged in a solution. The height that the solution reaches within the capillary is related to the surface tension by an equation discussed below.
- Stelagometer method: a weighting and reading method of a drop in a liquid.
- Fixed drip method: a method for determining surface tension and density by placing a drop in a substrate and measuring the contact angle (see fixed drip technique).
- Du Noüy-Padday Method: A minimised version of the Du Noüy method uses a small-diameter metal needle instead of a ring, in combination with a high-precision micro-balance to record the maximum hale. The advantage of this method is that very small volumes of samples (below some ten micro liters) can be measured with very high precision, without needing to correct by floating (for a needle or rarely, rod with own geometry). Beyond, the measurement can be performed very quickly, at least in about 20 seconds.
- Vibrational frequency of levitated drops: the natural frequency of vibrational oscillations of magnetic levitated drops has been used to measure superfluid surface tension 4He. This value is estimated at 0,375 dyna / cm to T = 0 K.
- Resonant oscillations of spherical and hemispheric liquid droplets: the technique is based on measuring the resonance frequency of spherical and hemispheric hanging drops managed in oscillations by a modulated electric field. Surface tension and viscosity can be evaluated from the resonant curves obtained.
- Gout bounce method: this method is based on aerodynamic levitation with a separable tober design. After dropping a drop stablely levitated on a platform, the sample is deformed and bounced back, oscillating in mid-air as well as trying to minimize its surface area. Through this oscillation behavior, the surface fluid tension and viscosity can be measured.
- Smartphone: Some smartphones can be used to measure the surface tension of a transparent liquid. The method is based on measuring the wavelength of known frequency capillary waves. The smartphone is located at the top of a cup with the liquid. Then, the smartphone vibro-motor excites (through the cup) capillary waves on the surface of the liquid, which are captured by the smartphone camera.
Effects
Liquid in vertical tube
Main article: Capillary action
An old-style mercury barometer consists of a vertical glass tube about 1 cm in diameter, partially filled with mercury, and with a vacuum (called a Toricelli vacuum) in the unfilled volume (see diagram below). the right). Note that the mercury level in the center of the tube is higher than at the edges, making the top surface of the mercury dome-shaped. The center of mass of the entire column of mercury would be somewhat low if the top surface of the mercury were flat over the entire cross section of the tube. But, the dome-shaped top gives slightly less surface area to the total mass of mercury. Again the two effects combine to minimize the total potential energy. Such a surface shape is called as a convex meniscus.
We consider the surface area of the entire mass of mercury, including the part of the surface that is in contact with glass, since mercury does not adhere to glass at all. So the surface tension of mercury acts over the entire surface area, including where it is in contact with the glass. If instead of glass the tube was made of copper, the situation will be very different. Mercury aggressively adheres to copper. So in a copper tube, the mercury level in the center of the tube will be lower than at the edges (ie it will be a concave meniscus). In a situation in which the liquid adheres to the walls of its container, we consider the part of the surface area of the fluid that is in contact with the container that has negative surface tension. The fluid then works to maximize the contact surface area. So in this case increasing the contact area with the container decreases, rather than increases, the potential energy. That decrease is enough to compensate for the increase in potential energy associated with lifting the fluid close to the container walls.
If a tube is narrow enough and the adhesion of liquid to its walls is strong enough, surface tension can pull liquid up the tube in a phenomenon known as capillary action. The height to which the column is raised is given by Jurin's Law:
h=2γ γ la# θ θ ρ ρ gr{displaystyle h={frac {2gamma _{la}cos theta }{rho g r}}}}
Yeah, θ θ {displaystyle theta } is greater than 90°, as with mercury in a glass container, the liquid will be depressed instead of lifted.
Puddles on a surface
Pouring mercury onto a flat horizontal sheet of glass results in a puddle that has a perceptible thickness. The puddle will spread out only to the point where it is a little less than half a centimeter thick, and no thinner. Again, this is due to the action of the strong surface tension of mercury. The liquid mass flattens out as it provides as much of the mercury to lower the level as possible, but the surface tension is, at the same time, acting to reduce the total surface area. The result of the compromise is a puddle of an almost fixed thickness.
The same demonstration of surface tension can be done with water, lime water, or even saline, but only on a surface made of a substance to which water does not adhere. Wax is such a substance. Water poured onto a smooth, flat, horizontal wax surface, such as a waxed sheet of glass, will act similarly to mercury poured onto glass.
The thickness of the pool of liquid on a surface whose contact angle is 180° is given by:
hp=2γ γ gρ ρ {displaystyle h_{p}=2{sqrt {frac {gamma }{grho }}}}}}}
In reality, the thickness of the puddle will be slightly less than predicted by the above formula, since very few surfaces have a 180° contact angle with any liquid. When the contact angle is less than 180°, the thickness is given by:
hp=2γ γ la(1− − # θ θ )gρ ρ {displaystyle h_{p}={sqrt {frac {2gamma _{la}(1-cos theta)}{grho }}}}}}}
| Stop. | t{displaystyle t} | γ γ {displaystyle gamma } | ρ ρ {displaystyle rho } | θ θ {displaystyle theta } | h{displaystyle h} |
|---|---|---|---|---|---|
| °C | din / cm | g/cm3 | ° | cm | |
| Mercury on glass | 487 | 13.5 | 140 | 0.36 | |
| Water on paraffin | 25 | 72 | 1.0 | 107 | 0.44 |
The formula also predicts that when the contact angle is 0°, the liquid will spread out in a micro-thin layer on the surface. Such a surface is said to be totally wetted by the liquid.
Breakdown of jets in drops
Main article: Plateau-Rayleigh instability
In day-to-day life, we all observe that a stream of water coming out of the valve will break into drops, no matter how soft the stream is emitted from the valve. This is due to a phenomenon called Plateau-Rayleigh Instability, which is entirely a consequence of surface tension effects.
The explanation for this instability begins with the existence of a small disturbance in the jet. It is always present, no matter how soft the stream. If the disturbances are resolved into a sinusoidal component, we will find that some components increase with time, while others decrease with time. Among those that grow over time, some grow at faster rates than others. Whether a component is increasing or decreasing, and how fast it is increasing is entirely a function of its wavenumber (a measure of how many peaks and valleys per centimeter) and the radii of the original cylindrical jet.
Thermodynamics
Surface tension thermodynamic theories
J. W. Gibbs developed the thermodynamic theory of capillary based on the idea of discontinuity surfaces. Gibbs considered the case of an acute mathematical surface being somewhere between the physical interface between two homogeneous substances. Given that the exact option of the location of the surface was somewhat arbitrary, it left it flexible. Since interference exists in thermal and chemical balance with the substances around it (with temperature T{displaystyle T} and potential chemicals μ μ i{displaystyle mu _{i}}), Gibbs considered the case where the surface should have excess energy, excess entropy and excess particles, finding it the natural free energy function in this case:
U− − TS− − μ μ 1N1− − μ μ 2N2...{displaystyle U-TS-mu _{1}N_{1}-mu _{2}N_{2}}}...,
an amount later called as the great potential and giving it the symbol Ω Ω {displaystyle Omega }.
Considering a sub-volumen V{displaystyle V} given containing a discontinuity surface, the volume is divided by the mathematical surface in two parts A{displaystyle A} and B{displaystyle B}, with volumes VA{displaystyle V_{A}} and VB{displaystyle V_{B}} with V=VA+VB{displaystyle V=V_{A}+V_{B}} Exactly. Now, if both sides A{displaystyle A} and B{displaystyle B} homogeneous fluids (with pressures) pA{displaystyle p_{A}}, pB{displaystyle p_{B}}) and remain exactly homogeneous to the mathematical edge, without any superficial effect, the great total potential of this volume could simply be − − pAVA− − pBVB{displaystyle -p_{A}V_{A}-p_{B}V_{B}}. The surface effects of interest are the modifications to this, and can all be collected in the term surface-free energy Ω Ω s{displaystyle Omega _{s}}, so the large total volume potential is:
Ω Ω =− − pAVA− − pBVB+Ω Ω s{displaystyle Omega =-p_{A}V_{A}-p_{B}V_{B}+Omega _{s}}.
For sufficiently macroscopic and smoothly curved surfaces, the surface free energy must simply be proportional to the surface area:
Ω Ω s=γ γ A{displaystyle Omega _{s}=gamma A},
for surface tension γ γ {displaystyle gamma } and surface area A{displaystyle A}.
As said above, this implies the mechanical work necessary to increase the surface area A{displaystyle A} That's it. dW=γ γ dA{displaystyle dW=gamma dA}assuming that the volumes on each side do not change. Thermodynamics requires systems to retain constant chemical potential and temperature, any spontaneous change in status is accompanied by a decrease in this free energy Ω Ω {displaystyle Omega }, that is, an increase in total entropy takes into account the possible movement of energy and particles from the surface in the fluids around. From this it is easy to understand because decreasing the surface area of the fluid mass is always spontaneous, provided is not coupled with any other energy change. Follow what in order to increase the surface area, a certain amount of energy must be added.
Gibbs and other scientists have fought arbitrariness in the exact microscopic location of the surface. For microscopic surfaces with very tight curvatures, it is not correct to assume the surface tension is independent of size, and topical as the Tolman length comes to take part. For a measured macroscopic surface (and flat surfaces), surface location has no significant effect on γ γ {displaystyle gamma }, however, has a very strong effect on surface entropy values, excess surface density of mass and internal surface energy, which are the partial derivatives of the surface voltage function γ γ (T,μ μ 1,μ μ 2,...){displaystyle gamma (T,mu _{1},mu _{2},...}.
Gibbs emphasized that for solids, the surface free energy must be completely different from the surface stress (what he called surface tension): the surface free energy is the work required to form the surface, while the surface stress is the work required to stretch the surface. In the case of the interface of two fluids, there is no difference between forming and stretching, since fluids and surfaces completely fill their nature when the surface is stretched. For a solid, stretching the surface, even elastically, results in a fundamentally changed surface. Further, the surface stress in a solid is a directional quantity (a tensile stress) while the surface energy is scalar.
Fifty years after Gibbs, J. D. van der Waals developed the theory of capillary effects based on the hypothesis of continuous density variation. He added to energy density the term c(► ► ρ ρ )2{displaystyle c (nabla rho)^{2}}Where c{displaystyle c} is the coefficient of capillary and ρ ρ {displaystyle rho } It's density. For multifaceted equilibrium, the results of van der Waals approximation almost match the Gibbs formula, but to model the phase transition dynamic of van der Waals approximation is much more convenient. The van der Waals capillary energy is now widely used in the multiphase flow phase field models. Such terms are also discovered in the dynamics of non-balance gases.
Bubble thermodynamics
The pressure inside an ideal spherical bubble can be derived from free energy thermodynamic considerations. The free energy above can be written as:| Free energy | Volume | Area | |
|---|---|---|---|
| Formula | Ω Ω =− − Δ Δ PVA− − pBV+γ γ A{displaystyle Omega =-Delta P V_{A}-p_{B}V+gamma A} | VA=43π π R3{displaystyle V_{A}={frac {4}{3}}pi R^{3}}} | A=4π π R2{displaystyle A=4pi R^{2}} |
| Substitute (Ω Ω =0{displaystyle Omega =0}) | 0=− − Δ Δ PVA− − pBV+γ γ A{displaystyle 0=-Delta P V_{A}-p_{B}V+gamma A} | ||
| Clearing | Δ Δ PVA+pBV=γ γ A{displaystyle Delta P V_{A}+p_{B}V=gamma A} | ||
| Deriving | Δ Δ PdVA=γ γ dA{displaystyle Delta P dV_{A}=gamma dA} | dVA=4π π R2dR{displaystyle dV_{A}=4pi R^{2}dR} | dA=8π π RdR{displaystyle dA=8pi R dR} |
| Replacement | Δ Δ P(4π π R2dR)=γ γ (8π π RdR){displaystyle Delta P (4pi R^{2}dR)=gamma (8pi R dR)} | ||
| Simplifying | Δ Δ P=2γ γ R{displaystyle Delta P={frac {2gamma }{R}}}} | ||
Which is equivalent to the Young-Laplace equation when Rx=Rand{displaystyle R_{x}=R_{y}}.
Influence of temperature
Surface tension is dependent on temperature. For this reason, when a value is given for the surface tension at an interface, the temperature must be stated explicitly. The general trend is that the surface tension decreases with increasing temperature, reaching a value of 0 at the critical temperature. For further details see Eötvös rule. There are only empirical equations for the relationship surface tension and temperature:
Eötvös equation
γ γ V2/3=k(Tc− − T){displaystyle gamma V^{2/3}=k(T_{c}-T)}
A typical value is k{displaystyle k} = 2.1 x 10-7 J/K mol2/3). For water one can use V{displaystyle V} = 18 ml / mol y Tc{displaystyle T_{c}} = 647 K (374 °C). A variant of Eötvös is described by Ramay and Shields:
γ γ V2/3=k(Tc− − T− − 6){displaystyle gamma V^{2/3}=k(T_{c}-T-6}}
Where the compensatory temperature of 6 K provides a formula with a better fit to reality at low temperatures.
Guggenheim-Katayama Equation
γ γ =γ γ or(1− − TTc)n{displaystyle gamma =gamma ^{o}{Bigl (}1-{frac {T}{T_{c}}}{Bigr)}{n}}}
This equation was also proposed by Van der Waals, who later proposed that the value of γ γ or{displaystyle gamma ^{o}} could be given by the expression:
γ γ or=K2Tc1/3Pc2/3{displaystyle gamma ^{o}=K_{2} T_{c}^{1/3} P_{c}{2/3}
| n{displaystyle n} | for |
|---|---|
| 11/9 | Organic liquids |
| 8 | Water |
| 1 | Liquid metals |
Both Eötvös and Guggenheim-Katayama take into account the fact that surface tension reaches 0 at critical temperature, which Ramay and Shields failed to match reality at this end point.
Influence of solute concentration
Solutes can have different effects on surface tension depending on the nature of the surface and the solute:
| Effect | Example |
|---|---|
| Small or no effect | Sugar in water/air.
Many organic compounds in oil/air. |
| Increase of surface tension | Many inorganic salts in water/air. |
| Non-monotonous change | Many inorganic acids in water/air. |
| Progressive surface tension decrease | Many amphilis, for example: alcohols in water/air. |
| Decrease of surface tension to a certain critical concentration and no effect afterwards | Surfactants forming micelas. |
Complicating the effect is that a solute can exist in a different concentration on the surface of a solvent than it does in the whole. This difference varies from one solute-solvent combination to another.
The Gibbs isotherm states that:
Interpreter Interpreter =− − 1RT(▪ ▪ γ γ ▪ ▪ ln C)T,P{displaystyle Gamma =-{frac {1}{RT}}{Bigl (}{frac {partial gamma }{partial ln C}}{Bigr)}}}_{T,P}}}}
Certain assumptions are taken into account in its derivation, so the Gibbs isotherm can be applied only to ideal (very dilute) solutions with two components.
Influence of particle size on vapor pressure
See also: Gibbs-Thomson Effect
The Clausius-Clapeyron relation leads us to another equation, also attributed to Kelvin, as the Kelvin equation. Explain why, since the surface tension, the vapor pressure for small drops of liquid in suspension is greater than the standard vapor pressure of that same liquid when the interface is planar. It is to say that when the liquid is forming small droplets, the equilibrium concentration of its vapor around it is higher. This rises, since the pressure inside the drop is greater than outside.
PVforg=PVoreV2γ γ /(RTrk){displaystyle P_{V}^{fog}=P_{V}{o}e^{V2gamma /(RTr_{k}}}}}}}}
The effect explains the supersaturation of vapors. In the absence of nucleation sites, small droplets must form before they can become large droplets. This requires a vapor pressure several times the vapor pressure at the phase transition point.
This equation is also used in catalyst chemistry to evaluate mesoporosity for solids.
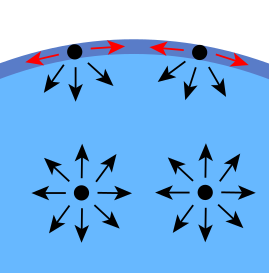
The effect can be seen in terms of the average number of molecular neighbors to surface molecules (see diagram).
The table shows some calculated values of this effect for water at different drop sizes:
| PPor{displaystyle {frac {P}{P_{o}}}}} water drops from different radius to STP | ||||
|---|---|---|---|---|
| Gout radio (mm) | 1000 | 100 | 10 | 1 |
| PPor{displaystyle {frac {P}{P_{o}}}}} | 1.001 | 1.011 | 1.114 | 2.95 |
The effect is clear for very small droplets, so a 1 mm radius droplet has about 100 molecules inside, which is a small enough amount to require quantum mechanical analysis.
Surface tension of water and seawater
The two most abundant liquids on Earth are fresh water and salt water. This section gives reference data correlations for the surface tension of both.
Surface tension of water
The surface tension of pure liquid water in contact with its vapor has been given by IAPWS as:
γ γ w=235.8(1− − TTc)1.256[chuckles]1− − 0.625(1− − TTc)]{displaystyle gamma _{w}=235.8{Bigl (}1-{frac {T}{T_{c}}}{Bigr)}{1.256}left[1-0.625{Bigl (}1-{frac {T}{T}{Bigr)}}}{right mN / m,
The validation region of the liquid-vapor saturation curve, from the triple point (0.01 °C) to the critical point. It also provides reasonable results when extrapolated to metastable (supercooled) conditions, below at least -25 °C. This formulation was originally adopted by IAPWS in 1976 and was adjusted in 1994 to correspond with the 1990 International Temperature Scale.
The uncertainty of this formulation is given over the total temperature range by IAPWS. For temperatures below 100 °C, uncertainty is ± ± {displaystyle pm }0.5%.
Seawater surface tension
Nayar et al. published baseline data for surface seawater tension over a salinity range of 20 ≤ ≤ S≤ ≤ {displaystyle leq Sleq } 131 g/kg and a temperature range of 1 ≤ ≤ t≤ ≤ {displaystyle leq tleq } 92 °C atmospheric pressure.. The temperature and salinity range encompasses both, the oceanographic range and the range of conditions found in thermal desalination technologies. The uncertainty of the measurements varies from 0.18 to 0.37 m N / m with an average uncertainty being 0.22 m N / m.
Nayar et al. They correlated the data with the following equation:
γ γ sw=γ γ w[chuckles]1+(3.66× × 10− − 4)S+(2.347× × 10− − 6)St]{displaystyle gamma _{sw}=gamma _{w}[1+(3.66 times 10^{-4})S+(2.347 times 10^{-6})St]}
The mean absolute percentage deviation between measurements and correlation was 0.19% while the maximum deviation is 0.60%.
The International Association for the Properties of Water and Steam (IAPWS) has adopted this correlation as an international standard guide.
Tabulated data
Surface tension of various liquids in din/cm against air
Mix compositions are denoted by "%" they are by mass
din/cm is equivalent in SI units to mN/m (millinewton per meter)
| Liquid | Temperature (°C) | Tension Surface γ γ {displaystyle gamma } |
|---|---|---|
| Acetic acid | 20 | 27.60 |
| Acetic acid (45.1 %) + water | 30 | 40.68 |
| Acetic acid (10.0 %) + water | 30 | 54.56 |
| Acetona | 20 | 23,70 |
| Blood | 22 | 55.89 |
| Dietil éter | 20 | 17.00 |
| Etanol | 20 | 22.27 |
| Ethanol (40 %) + water | 25 | 29.63 |
| Ethanol (11.1 %) + water | 25 | 46.03 |
| Glicerol | 20 | 63.00 |
| n-Hexano | 20 | 18.40 |
| Hydrochloric acid 17.7 M aqueous solution | 20 | 65.95 |
| Isopropanol | 20 | 21.70 |
| Helio II liquid | -273 | 0.37 |
| Liquid nitrogen | - 196 | 8.85 |
| Liquid oxygen | -182 | 13.2 |
| Mercury | 15 | 487.00 |
| Methanol | 20 | 22.60 |
| melted silver chloride | 650 | 163 |
| Sodium chloride / melted calcium chloride (47 / 53 mol %) | 650 | 139 |
| n-Octane | 20 | 21.80 |
| Sodium chloride 6.0 M aqueous solution | 20 | 82.55 |
| Sacarous (55%) + water | 20 | 76.45 |
| Water | 0 | 75.64 |
| Water | 25 | 71.97 |
| Water | 50 | 67.91 |
| Water | 100 | 58.85 |
| Tolueno | 25 | 27.73 |
| Benceno | 28,85 | |
| Carbon tetrachloride | 26,95 | |
| Acetato de eilo | 23.9 | |
| Ethyl ether | 17,01 |
Contenido relacionado
Darmstatio
William Hyde Wollaston
Gunpowder


































































































![{displaystyle gamma _{w}=235.8{Bigl (}1-{frac {T}{T_{c}}}{Bigr)}^{1.256}left[1-0.625{Bigl (}1-{frac {T}{T_{c}}}{Bigr)}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ad3d17afa88d11e8989c6ed9ae28315945d8fac)



![{displaystyle gamma _{sw}=gamma _{w}[1+(3.66 times 10^{-4})S+(2.347 times 10^{-6})St]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3459f52cc451a53b02eada3d269c0205d7a0aadc)