Sundial

Artistic sun watch designed by Jean Picard and located on the frontón de la Sorbonne

The sundial or sundial is an instrument used since ancient times to measure time. In Spanish it is also called solar quadrant. It uses the shadow cast on a surface with a scale to indicate the position of the Sun in the diurnal movement. Depending on the layout of the gnomon and the shape of the scale, different types of time can be measured; the most common is apparent solar time (King Ahab's sundial).

History

The documented beginnings

Egyptians' knowledge of astronomy allowed them to orient the pyramid of Cheops, c. 2550 B.C. C. through stellar references. A thousand years later, at the time of Pharaoh Tutmosis III (c. 1500 BC), an instrument called sechat is designed; It is a small sundial to measure time by the length of the shadows, which consisted of two prismatic, stony pieces, about three decimeters long, located perpendicularly, where one had the hours marked and the other served as needle. It must have been a very popular instrument among the Egyptian priests, because, due to its dimensions, it may have been a portable instrument.

Circa 2400 B.C. C. Sumerian scribes already used a calendar: they divided the year into 12 parts, they also divided the day, and they did so following the same pattern of divisions. His year consisted of 12 months and each of them 30 days. His days consisted of twelve danna (each danna would last two of our hours) of 30 ges each (each ges would last 4 of our minutes).

Most of the instruments used in ancient times were not portable. In Mesopotamia we find ziggurats, which were constructions with steps in which the hours could be visualized by counting the steps that were obscured by the shadow of their own edges. The first known literary reference to a sundial is the famous Quadrant of Achaz around the 7th century BC. c.

Baelo Claudia Solar Clock, 1st Century (Cadiz)

Greco-Roman Period

The perception of time in Greek society in the 5th century B.C. C. is evident from the reading of various Greek and Roman writers of the time who describe, and give references to, instruments identified as the first sundials. The oldest Greek author, and perhaps the most important, has been Herodotus of Halicarnassus (484-426 BC), who makes a brief review in his History (II, 109, 3) of Greek knowledge of time, saying that they acquired the division of the day into twelve parts from the Babylonians.

Therefore, the time system of the Greeks was temporary: by this it is meant that the hour was understood as the twelfth part of the diurnal arc traveled by the Sun, but since such an arc varies during the year, the hour also it varies. For this reason, this system is also called unequal hours. The Romans, in turn, inherited this system of dividing the day from the Greeks.

Pliny the Elder (ca. 23-79) in his Natural History (Book XXXVI, Chapter XIV) tells the story of the clock that Emperor Augustus had built on the Field of Mars, taking advantage of a Egyptian obelisk of the pharaoh Psamético II, the so-called Sundial of Augustus.

To the obelisk that is in the Field of Mars, the divine Augustus attributed to him the admirable function of measuring the shadow projected by the Sun, thus determining the duration of the days and nights: he placed plates that were in proportion to the height of the obelisk, so that in the sixth hour of the winter solstice the shadow was as long as the plates, and slowly diminished by day to see the stones being inserted. It added, on the end, a golden ball that projected a defined shadow, because if not the sharp end of the obelisk would have cast an imprecise shadow (it is said that it took the idea of the human head). After thirty years these measures were wrong. The cause is not known: perhaps the course of the Sun has not remained the same, or has changed for some astronomical reason, or because the whole earth has moved or simply because the gnomon has moved due to thermorial shakes, or because the avenues of the River Tiber have caused a descent of the obelisk.

At the end of the first century B.C. C. and Emperor Augustus was already reigning in Rome, a military engineer named Marco Vitruvio Pollio wrote the only treatise on architecture that, from antiquity, has come down to us. It is known that he was an architect in Rome, where he built and directed various works, including the Basilica of Fanum. The treatise is divided into ten books and is entitled De Architecture. The first seven books deal with architecture, the eighth with hydraulic constructions, with special application to the methods for lighting and conducting water, the ninth with gnomonics, and the tenth with machinery. In Book IX, Chapters VIII-IX he describes a geometric method for designing sundials called an analemma. The author does not claim the invention of this method, but assigns it to what he calls his masters.

Medieval times

In the first centuries of the Christian era, the gnomonic, dimly illuminated by the studies of Hellenic astronomy, enters a decadence that characterizes all the science of cultural and economic Europe of the Middle Ages. There are few elements (especially archaeological) that we can find: there are hardly any writings that show new advances.

Although the measurement of time was of little interest to the general population in this period, there are no precise scientific descriptions either. However, as rarities of the time, there are the surveyors Bede the Venerable and Higinio Gromático (II century).

Palladium in the IV century writes a work called Re Agrícola composed of fourteen books, divided in such a way that each book corresponds to the typical agricultural tasks of each month. At the end of each book he puts a kind of table that he calls horologium typical of the month in question. In said horologium it indicates the length of the shadows in feet for each hour during the days of the month in question. It thus indicates the use that was made of the human body to replace sundials. In gnomonic they are called grandfather clock.

In the 7th century the Benedictine orders became important. In the year 529, the founder of this religious order, Saint Benedict, prescribed from his monastery some precise Rules by which all Benedictine monks in Europe must abide. From its origins, the Catholic Church wanted to sanctify certain hours of the day with a common prayer. Saint Benedict called these hours of prayer "canonical hours", and this was the case since the sixth century. The name comes from the norms or canons provided by the Church.

The gnomonics of these centuries led to the construction of mass clocks or clocks of canonical hours, in which the hours of prayer were indicated. These clocks are generally located on the southern facades of churches or monasteries. Personal watches were also developed for this purpose, such as the ring watch.

In this medieval period, in which the gnomonic "official" was the one imposed by the Catholic Church, through the use of canonical hours, there were innovative authors such as Cayo Julio Solino who in the IV century wrote a book entitled Tractatus de umbra et luce ('Treatise on Shadow and Light') that maintains the link of knowledge of Greco-Roman culture. There is also another obscure author of the VI century, Anthemius, who is credited with the codex entitled Problema Sciatericum.

Already at the beginning of the century I the studies carried out on the works of Vitruvius and Ptolemy allow us to recognize for the first time that there are two important parameters for the design of a sundial:

• Geographical latitudewhich determines the geographical location of the Earth where the clock will be installed. This leads to thinking that these authors knew that the Earth is not flat, because the determination of its value depends on the angular distance of the clock's location with respect to the Earth's equator, and that it was determined in the antiquity observing the duration of the day and the length of the equinoccial shadow of the gnomon at noon (gnomonis aequinoctialis); both functions determine geographical latitude in one way.
• The obliqueness of the ecliptic; parameter that did not depend on the geographical location of the solar clock and which was mistakenly supposed to be an invariable constant in time. Eudemus de Rodas (320 BC) was the first to observe (not measure) the obliqueness of the ecliptic. The later astronomers determined their value in 1/15 of a circle, and Hiparco de Nicea adopted a better value of 11/83 parts of the semi-circle. The first of the values is that used by Vitrubio in the construction of its analytics.

Arab boom

In the 9th century, Arab astronomy entered the scene. The Al-Mamun caliphate marks the beginning of an intense cultural activity that would continue in successive centuries with authors such as Averroes, Thábit Ibn Qurra (826-901), Costa Ebn Luca, Abulphetano, Hazemio, Al-Biruni (973-1048). While the Christian Europe of the time followed the work of the venerable Bede, the Arabs had a very hectic intellectual activity continued since the destruction of the Library of Alexandria. It is only from the 10th century onwards that Europe begins to timidly see the immense work of compiling ancient knowledge carried out by the Arabs.

The Arab clocks of this medieval period were all flat, at least for the most part, and were called al-basit ('flat surface'); they were built in marble (Ruchâmet), or in copper plates. All of them were without inclusions of spherical elements, and with an indication of the direction of the Kaaba sanctuary in Mecca, due to the religious precept of praying with the face directed towards that place regardless of where it was located. Such a direction is called Al Qibla. All of them with curious curves for daily prayers.

In the year 1000 in Spain the Quadrans vetus cum cursorem was used for the first time, the inventor of which is unknown. But this quadrant will be the first outpost of the navigation instruments that Christopher Columbus will use.

It was Ermanno Contratto (1013-1054), a German mathematician who knew the Arabic language, who wrote the first treatise on the astrolabe around the year 1026, preserving some of the Arabic terminology. In this book De mensura astrolabii liber there are some indications for making the shepherd's watch. In the field of gnomonics, the translation of two Arabic codices was the most important point of cultural transfer.

In Spain, the King of León and Castile Alfonso X nicknamed "el Sabio" (1224-1284) brought together in the city of Toledo a large group of Christian, Greek and, Hebrews and Arabs. With this mix of scholars he was able to translate into Latin a large part of the works written in Arabic. In this way, the door of Arab knowledge from the previous centuries to Europe will be opened even more. It goes without saying that this phenomenon allowed the European gnomonic to get out of the medieval delay in which it was immersed. However, this absorption was slow.

At the beginning of the 14th century, mechanical instruments capable of regularly measuring time during the day appeared. In this way, in the year 1386, a clock was placed in Salisbury Cathedral and in 1400, during the reign of Henry III "the Mourner", it was installed in Seville, in the tower of the church of Santa María, the first mechanical clock with bells.

Renaissance

Among the masterpieces in the field of time measurement, it is worth highlighting art jewels such as the Sundial by Schniep, a German Renaissance craftsman, obtained by Fernando Álvarez de Toledo y Pimentel (1507-1582), third Duke of Alba, in 1545.

Many sundials were also built in the European colonies of the Americas, some of which are still standing today. In the case of the Intertropical zone, they must be built with a double hour disk, like the one seen in the image: the disk that is to the south (the one that appears in the photo) is used during part of the year (August to April) and the disk on the other side, which faces north, would be used the rest of the year, when the sun is between the latitude of La Asunción (Margarita Island, Venezuela) and the Tropic of Cancer. Two days a year, at the end of April and the beginning of August, the sun passes through the vertical of the place (the zenith) and then, as is logical, the hours can be seen on both sides.

Types of sundials

Precision sunglasses in Bütgenbach, Belgium. (Precision = ±30 seconds) 50°25′23′′N 6°12′06′E / 50.4231, 6.2017 (Belgium) (Google Earth).

Sunglasses in St. Rémy de Provenza. The sign says: "IL Est TOUJOURS L'HEURE de ne Rien FAIRE" (it is always time to do nothing)

There are different types of sundials; some of them are:

Equatorial Clock

Equatorial watch position outline

Scheme of the equatorial quadrant

In this model, the gnomon casting the shadow has the following spatial orientation:

• It is parallel to the axis of rotation of the Earth.
• It is contained in the meridian plane of the place.
• Shape with the horizontal plane an angle equal to the latitude of the place.

To determine the direction of the meridian plane of the place to later place the gnomon, it is best to determine the meridian of the place, that is, the intersection of said meridian plane with the horizontal plane. The meridian coincides with the SOUTH-NORTH direction. The meridian of the place also coincides with the shadow produced by a rod placed vertically at the moment the Sun passes through the meridian of the place (at that moment the Sun is located towards the south, in the northern hemisphere, and towards the north in the southern hemisphere and at the highest point of its daily trajectory). To find out at what official time this situation occurs, it is possible to resort to the ephemeris tables of the official observatories.

The surface on which the shadow is cast is flat and perpendicular to the gnomon and therefore parallel to the equator. The drawing of the hour lines is simple. In the quadrant, a circle is drawn with the center at the pole of the quadrant and said circle is divided into 24 parts of 15º each and later the 24 radii corresponding to the previous division are drawn. Of all of them, the radius that coincides with the intersection of the meridian plane of the place with the plane of the dial and that goes towards the horizon is the 12:00 hour line. The different radii spaced 15 by 15º indicate the hours before 12 o'clock when they are west of the 12 o'clock line and the hours after when they are east of the 12 o'clock line. It is not necessary to plot all the radii, since the hours before 4 o'clock and after 8 o'clock are not necessary. The 6:00 and 18:00 radii determine the east–west direction if the dial is oriented correctly.

For half a year, from the beginning of spring to the end of summer, a period during which the solar declination is positive, the shadow of the gnomon is projected on the upper face of the equatorial plane of the place. During the other half year the shadow appears on the underside and therefore it is necessary:

1. mark the hourly straights on both sides of the surface that makes of equatorial plane of the place, e
2. install that surface at a certain height to be able to observe comfortably both sides.

Landscape

Horizontal clock, figure 1

Horizontal clock, figure 2

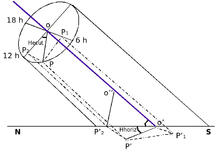
The horizontal sundial is obtained by the oblique orthogonal projection of the hour lines of an equatorial clock onto a horizontal plane.

The time lines of the equatorial clock are uniformly distributed and also the hour angle of each equatorial hour (Hecut) increases by 15º by 15º to the left and right of the 12 o'clock time line.

The time line of 12 in the morning is contained in the meridian plane of the place. Thus, the hour angle for 11 in the morning would be Hecut=15º, for 10 in the morning Hecut=30º and so on.

In addition, the gnomon of the equatorial clock, which is perpendicular to the plane of the equatorial clock, is parallel to the terrestrial axis and therefore forms an angle with the horizontal plane that coincides with the latitude Φ of the place of settlement of the equatorial clock and is contained in the meridian plane of the place.

• Coordinates of point P end of an equatorial clock timeline:

Point P represents the end of a time line of the equatorial clock (in the figure it could be the one relative to 11:00). If we choose a Cartesian coordinate system so that the X axis coincides with the straight line that contains the time lines of 6:00 p.m. and 6:00 a.m. and with a positive sense, the one that results when going from the end of 6:00 p.m. to the end of 6:00 a.m. and as Y axis the line that contains the 12:00 line and with a positive sense the one that results from going from the center O to the end of 12:00, then the coordinates of point P would be:

OP1 = x = R equatorial sen

OP2 = y = R cos ecuatorial

R represents the radius of the circle that passes through the ends of the hour lines of the equatorial clock.

• Orthogonal oblique projection, e.g. Hecut=15o timeline:

Coordinates of point P' end of the corresponding hour line of the horizontal clock: the extreme point P is projected on the point P', whose coordinates are obtained by making the oblique orthogonal projection on the horizontal plane: The segment OP1 is on the X axis and is parallel to the horizontal plane (see figure 2) where the oblique orthogonal projection is made, therefore, the projection O'P'1 coincides with the projected segment OP1.

The oblique orthogonal projection of the segment OP2, which is on the Y axis, on the horizontal plane is larger and specifically turns out to be the hypotenuse of the triangle P'2 O' O" and consequently O' P'2=R. cos Hecut)/ sin Φ. Therefore, the coordinates of P' will be:

O'P'1 = x' = OP1 = R sen Hecut

O'P'2 = y' = (R cos Hecut)/sen Ω

Sunglasses at the Nautical Museum of the Aegean Sea (Mýkonos -Greece-).

• Angle of the Hhorizontal hour lines of the horizontal clock with the meridian line:

The angle formed by the new horizontal hour lines with the meridian line (that is, with the 12 o'clock hour line), will have a tangent that fulfills the relationship:

 x' R sen Hecut

So Hhorizontal = --- = ---------------------- = so Hecut · sen

 y' (R cos hecut) / sen Ω

• Position of gnomon on the horizontal clock:

The oblique orthogonal projection of the gnomon coincides with O'. The direction of the gnomon must remain parallel to the terrestrial axis and therefore it will continue to form an angle Φ with the horizontal and at the same time contained in the meridian plane of the place. In short, it is an extension of the equatorial clock gnomon.

Analemmatic

Anal watch

Analematic watch: detail of the projection of the shadow on the time ellipse on the IES analematic clock The Calls de Santander (Cantabria, Spain). Coordinates: 43.47315289163033, -3.793039682410239.

It is a sundial with an elliptical horizontal dial associated with a vertical mobile gnomon along the minor axis of the ellipse, said minor axis being in a NORTH-SOUTH direction. The dial is built directly on the ground and in this case it will be the observer himself who, acting as a mobile gnomon, moves to certain positions on the minor axis of the ellipse depending on the date, from which he projects his shadow onto the ellipse.. The starting point is the equatorial dial clock.

A sundial of this type can be found in Puerto de Cotos (Madrid, Spain), about 300 meters north of the highway, and another in the town of Alfambra in the province of Teruel. In this sundial, the indication of the days and months on the ground (where the observer stands to see the time indicated by the projection of his own shadow) is accompanied by the signs of the Zodiac, which is reason for confusion because people do not usually identify that they are in front of a sundial. And in this case, we have to consider the legal time in Spain, which is one hour after solar in winter and two hours later in summer.

Verticals

The time lines of a non-declining vertical clock are calculated through an oblique orthogonal projection of the time lines of an equatorial clock onto a vertical plane.

Screening of the vertical sun clock.

Aldeburgh, Suffolk, England.

Cape Town, South Africa (South Hemisphere)

The time lines of the equatorial clock are uniformly distributed, and also the hour angle of each hour (Hecut) increases by 15º by 15º to the left and right of the 12 o'clock time line. The time line of 12 in the morning is contained in the meridian plane of the place. Thus, the hour angle for 11 in the morning would be Hecut=15º, for 10 in the morning Hecut=30º and so on. In addition, the gnomon of the equatorial clock, which is perpendicular to the plane of the equatorial clock, is parallel to the terrestrial axis and therefore forms an angle complementary to the latitude Φ of the place of settlement of the equatorial clock with the vertical plane, that is, 90º- Φ and it is also contained in the meridian plane of the place.

• Coordinates of point P end of an equatorial clock timeline:

Point P represents the end of a time line of the equatorial clock (in the figure it could be the one relative to 11 o'clock). If we choose a Cartesian coordinate system so that the X axis coincides with the straight line that contains the hourly lines at 6:00 p.m. and 6:00 a.m. Y axis the straight line that contains the 12 o'clock line and with a positive sense the one that results from going from the center O to the end of 12 o'clock, then the coordinates of point P would be:

OP1 = x = R.sen Hecut

OP2 = y = R.cos Hecut

R represents the radius of the circle that passes through the ends of the hour lines of the equatorial clock.

• Coordinates of point P' end of the corresponding Hvertical timeline of the vertical clock:

The extreme point P is projected on the point P', whose coordinates are obtained by performing the oblique orthogonal projection onto the vertical plane. The OP1 segment lies on the X axis and is parallel to the vertical plane on which the oblique orthogonal projection is made; therefore, the projection O'P'1 coincides with the projected segment OP1.

The oblique orthogonal projection of the segment OP2, which is on the Y axis, on the vertical plane is larger and specifically turns out to be the hypotenuse of the triangle P'2 O' OR and consequently

O' P'2=R. cos Hecut)/ sen (90o -Ω)

therefore, the coordinates of P' will be:

O'P'1 = x' = OP1=R.sen Hecut

O'P'2 = y' = (R. cos Hecut)/ sen (90o-Ω)

• Angle of the hourly straights of the vertical clock:

The angle formed by the new vertical hour lines (Hvert) with the 12 o'clock line (the 12 o'clock line is the vertical line that passes through the pole), will have a tangent that satisfies the relationship:

 x' R.sen Hecut
so Hvert = --- = ------------------- = so Hecut · sen (90o-Ω) = so Hecut · cos Ω
and' (R. cos Hecut)
-...
sen (90o-)

• Position of the gnomon on the non-declining vertical clock

The oblique orthogonal projection of the gnomon coincides with O'. The direction of the gnomon must remain parallel to the terrestrial axis and therefore it will continue to form an angle (90º-Φ) with the vertical plane and at the same time contained in the meridian plane of the place. In summary, the position coincides with the extension of the gnomon of the equatorial clock.

Oriented

Declining

Laptops

Shepherd's

Graphic representation of the shepherd's watch

Daily solar cycle on the shepherd's watch

Curves that are drawn on the cylinder.

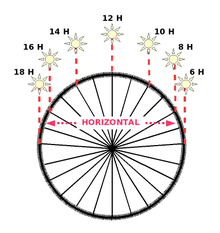
The portable cylindrical sundial, called shepherd's (used by shepherds in the Pyrenees and the Alps), measures the inclination of the sun, which varies according to latitude for the same instant of day and year. Therefore, each clock must be built for a certain latitude. At the time of the passage of the sun through the local meridian (true noon), its height varies with respect to the horizon according to the seasons. As an example, for a place located at 42° latitude (north or south):

• Summer Solstice: 42° above horizon + 23° 27'=65° 27'

• Equinox: 90° - latitude = 42° above the horizon

• Winter Solstice: 42° above the horizon - 23° 27'=18° 33'

Throughout the day, the height of the sun varies depending on the time of day.

At Earth's equator:

• At noon: for a time angle (AH)=0, the inclination of the sun is 90° - 0°=90° compared to the horizontal of the place.

• At 10:00: for a time angle (AH)=30o, the inclination of the sun is 90o - 30o=60o regarding the horizontal of the place.

• At 0800: for a time angle (AH)=60o, the inclination of the sun is 90o - 60o=30o regarding the horizontal of the place.

The height of the sun (HS) at a specific time (AH=hour angle) is determined based on the position of the sun (declination depending on the date=D) and the latitude of the place (L).: HS (in degrees)= arcsine [(sin L sin D) + (cos L cos D cos AH)] The shepherd's clock-style shadow cast tells time based on the height of the sun at the time of measure. Since the height of the sun varies with the date, the cover of the clock must be turned until the position of the stylus coincides with the date of the day and orient the cylinder towards the sun until a vertical shadow is obtained whose length will indicate the time in the pattern of curves of the cylinder. The relationship between the length of the style and the height of the sun is given by the formula:

Time = style length (ls) * so HS

Flat

Spherical

Negative

In conventional sundials the gnomon projects the shadow on a reference square, the negative sundial is the one that projects the light rays through a slit.

In the graphic on the right you can see the rays of light projected through the four domes on the wall facing south.

Negative sunglasses, Corregidora, Querétaro, Mexico.