Sudoku
Sudoku (Japanese: 数独, sūdoku) is a mathematical game that was invented in the late 1970s, gaining popularity in Japan in the 1970s. 1980, and became known internationally in 2005, when numerous newspapers began to publish it in their hobby section.
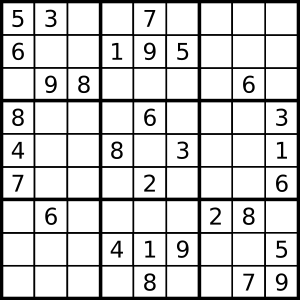
The object of Sudoku is to fill a 9 × 9 cell grid (81 cells) divided into 3 × 3 sub-grids (also called "boxes" or "regions") with the figures from 1 to 9 starting from some numbers already arranged in some of the cells. The initial form of the game is that there are nine different elements, which must not be repeated in the same row, column or sub-grid. A well-planned sudoku can only have one solution, and it must have at least 17 initial clues. The solution to a Sudoku puzzle is always a Latin square, although the converse is generally not true since Sudoku has the added restriction that the same number cannot be repeated in a subgrid.
History
In the 18th century the famous Swiss mathematician Leonhard Euler created a system of probabilities to represent a series of numbers without repeating. Due to this, Euler is considered the inventor of this game.
Already in 1970 the publishing house Math Puzzles and Logic Problems published a section called Number place so this mathematical enigma would become hobbies although years later it was lost in oblivion.
In 1984 the Japanese newspaper Monthly Nikolist published a hobby section called Sūji wa dokushin ni kagiru (数字は独身に限る) "numbers must be unique" (literally dokushin (独身) = "celibate, unmarried"). It was Maki Kaji, president of Nikoli, who named it. The name was shortened to Sūdoku (sū = number, doku = solo).
It became known internationally in 2005, when several newspapers began to publish it as a hobby.
Rules and Terminology
Sudoku is usually laid out as a 9 × 9 grid, made up of 3 × 3 sub-grids called "regions" (also called "boxes" or "blocks").
Some cells already contain numbers, known as "given numbers" (or sometimes "clues"). The goal is to fill the empty cells, with a number in each one, such that each column, row, and region contains the numbers 1–9 only once.
Also, each number in the solution appears only once in each of the three "directions", hence the "numbers must stand alone" which evokes the name of the game.
Solving methods
 The green box of the region 3 × 3 of the upper left corner should contain a 7.
The green box of the region 3 × 3 of the upper left corner should contain a 7.
The strategy for solving this puzzle can be thought of as a combination of three processes: tracking, marking, and analysis.
Tracking
In the example above, by scanning far and wide for 7s located anywhere on the grid, the player can remove all empty cells in the upper left corner that cannot contain a 7. This leaves only one possible cell (marked in green).
Marked
Scanning is interrupted when no new numbers can be discovered. At this point it is necessary to focus on some logical analysis. Most find it helpful to guide this analysis by marking candidate numbers in the empty cells. There are two popular notations: subscripts and periods.
In subscript notation, candidate numbers are written small in cells. The downside is that the original puzzles are published in newspapers that usually don't leave much room to accommodate more than a few digits. If this notation is used, solvers often create a larger copy of the puzzle and use a sharp pencil.
The second notation is a pattern of dots with a dot in the upper left corner representing a 1 and a dot in the lower right corner representing a 9. This notation has the advantage that it can be used in the original puzzle. Dexterity is required for the placement of the dots, because the existence of displaced dots or inadvertent marks inevitably leads to confusion and they are not easy to erase without adding further confusion.
Analysis
There are two main approaches:
- In eliminationprogress is made through the successive elimination of candidate numbers for one or more cells, to leave only one choice. After achieving each response, a new track must be done (usually checking the effect of the last number). There's a series of elimination tactics. One of the most common is the "borrowing of the non-concurring candidate". Cells with identical configuration of candidate numbers are said to match if the number of candidate numbers in each is equal to the number of cells containing them. This approach can be disapproved by logical purists for too much trial and error but can reach clear and fast solutions.
Ideally, you need to find a combination of techniques that avoids some of the drawbacks of the above elements. Counting regions, rows, and columns can be boring. Typing candidate numbers into empty cells can be very time consuming. The "what-if" It can be confusing unless you are well organized. The intent of the question is to find a technique that minimizes counting and marking.
A systematic analysis of logic and solving techniques was published in English: "Pattern-Based Constraint Satisfaction and Logic Puzzles".
Difficulty levels
Software that solves Sudoku puzzles can estimate the difficulty a human has in finding the solution, based on the complexity of the required solving techniques. This estimate allows publishers to tailor their Sudoku puzzles for people with different solving experience. Some "online" (online) also offer several levels of difficulty.
Construction
A sudoku must have a unique solution to be considered well posed; that is, from the initial clues there can only be one valid way to complete the remaining squares. For a sudoku to have a single solution, it is necessary that the number of initial clues be at least 17; this was demonstrated in 2012.
The construction of a sudoku game can be done by hand efficiently by predetermining the positions of the given numbers and assigning them values to carry out a deductive process.
Nikoli Sudoku puzzles are built by hand, and the author's name appears in the credits next to each puzzle; the given numbers are always in the form of a symmetrical pattern. Dell's Number Place Challenger puzzles (see Variants below) are also credited. The sudoku puzzles that appear in most UK newspapers are apparently computer generated, but they use probables in computer generated sudoku puzzles. The challenge for Sudoku programmers is to teach a program how to build intelligent puzzles in a way that is indistinguishable from those made by humans; It took Wayne Gould retouching his popular show for six years to believe he had reached that level.
Variants
Although most commonly the table is 9x9 in size with 3x3 regions, there are numerous variations. Starter games can be 4x4 boards with 2x2 regions; Under the name Logi-5, 5x5 tables have been published with pentominoes as regions; the World Puzzle Championship has published a 6x6 board with 2x3 regions and a 7x7 board made up of 6 regions made up of heptominoes and a separate region. Larger size tables can also be found. The Times newspaper proposes Dodeka Sudoku, a 12x12 board with 12 4x3 regions. Dell Magazines frequently publishes 16x16 sets (the 16x16 variant normally uses the symbols 1 through G, instead of the symbols 0 through F used in hexadecimal). The Nikoli puzzle editor proposes the Giant 25x25 Sudoku.
Another frequent variation is to add limits on the placement of numbers in addition to maintaining the normal requirements on rows, columns and regions. Boundaries often take the form of an extra "dimension"; the most common is to force the numbers on the main diagonal of the table to be unique. The aforementioned Number Place Challenger games include this variant. Also part of this variant are the Daily Mail games that use 6x6 boards.
The American newspaper USA Today publishes another variant called “Mini Sudoku”, consisting of a 6x6 table with 3x2 regions. The objective is the same as in the original Sudoku, but in this variant only numbers from 1 to 6 are used.
Another variant is the combination of Sudoku and Kakuro in a 9x9 table, called Cross Sum Sudoku, in which the clues are given through crossed sums. It is also possible that the clues are given by crypto-arithms in which each letter represents a single digit from 0 to 9. An example is: NUMBER+NUMBER=KAKURO whose only solution is 186925+186925=373850. Another example is SUDOKU=IS*FUNNY whose solution is 426972=34*12558.
Addoku combines elements of Sudoku and Kakuro – normally no starting numbers are given, but the 9x9 board is divided into regions, each of which contains the sum of all the numbers in the region also taking into account that there are no repeat numbers in the same region. When completing the table, the original Sudoku rules are also maintained.
One of the most popular variants is Hypersudoku. It is published in newspapers and magazines all over the world and is also known by “Sudoku NRC Handelsblad”, “Windoku”, “Hyper-Sudoku” and “Sudoku 4 squares”. The base is identical to that of the original Sudoku, but it includes additional interior areas where numbers from 1 to 9 must appear. The algorithm that solves it is slightly different from normal Sudoku due to the influence of the overlapping squares. This overlap gives the player more information which allows them to reduce the chances of the remaining squares. The way of playing is similar to that of Sudoku but it is necessary to pay more attention to the squares and overlapping areas than to the rows and columns.
Games built from multiple Sudoku tables are also common. In Japan, Sudoku Gattai 5 (mix of 5) is known, made up of 5 9x9 boards with overlapping corner regions in the shape of a quincunx. In newspapers such as The Times or The Sydney Morning Herald, this variant is known as Sudoku Samurai. Others such as the Baltimore Sun and the Toronto Star publish this variant in their Sunday edition under the name High Five. Often no clues are provided in the overlapping regions. Variants with sequential tables are also published, instead of overlapping ones, in which the values of certain positions are transferred from one table to another.
The Social Sudoku is a digital multiplayer version of Sudoku that allows 2 players to play at the same time on the same board. This variant was created by Crosswords Ltd. in 2010 and released as an app for Apple's iOS platform through its Game Center. Social Sudoku[2] awards points to each player as they place the numbers correctly, blocking the selected square from the other player. Incorrect moves result in the player not having access to the board for 10 seconds, as well as causing the loss of points.
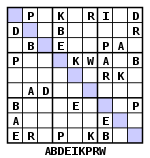
Alphabetic variants have also emerged, sometimes called Letter Sudokus (Wordokus): there is no functional difference unless the letters form words. Some variants, such as the one from TV Guide, include once the game is solved a word on the main diagonal, in a row or in a column; Determining the word in advance can be a help in solving the game. A Wordoku can contain other words besides the main word. As in the example on the right, the words “Kari”, “Park” and “Per” could be part of the solution. This should be avoided by replacing, for example, the character "R" with the character "Q". On the other hand, Sudoku Ripeto allows you to repeat symbols and Custom Sudoku shows words on the board before solving.
Another variant with no functional difference is the Quadratum Latinum with Roman Numerals from Hebdomada Aenigmatum, the crossword puzzle magazine entirely in Latin by Luca Desiata.
With a standard deck of 81 cards from the Set! Sudoku can be played. The three-dimensional version of Sudoku was invented by Dion Church and published in the Daily Mail Telegraph in May 2005. There is also a version of the Rubik's cube called the cuboku.
There are many other variants. Some feature different shapes in the layout of the 9x9 board overlaps, such as a butterfly, a windmill, or a flower. Other versions vary in the game's resolution logic. One of them is Sudoku Greater Than. In this version, each 3x3 region contains 12 greater (>) or lesser (<) symbols on the common line of two adjacent numbers. Another such variant is Sudoku No Hints in in which nine 9x9 Sudoku boards are placed in a 3x3 matrix. The center cell of each 3x3 region in each of the 9 tables is left blank, making a 10th Sudoku without any full cells; hence the name "no clues".
Contenido relacionado
Slovakia at the Olympics
Annex: Rowing at the 1980 Moscow Olympics
Los Angeles 1984 Olympic Games