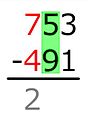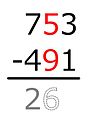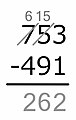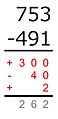Subtraction

"5 − 2 = 3" (verbally, "five less two equals three").

An example problem

0-10 numbers. Tag line = minuendo. axis X = subtracting. axis Y = difference..

Outdoor tent in Bordeaux advertising subtractions of 20% of the price of a second perfume

The subtraction or subtraction is an arithmetic operation that is represented with the sign (−); represents the operation to remove objects from a collection. For example, in the image on the right there are 5 − 2 peaches; meaning 5 peaches are 2 removed, so there are a total of 3 peaches. Therefore, 5 − 2 = 3. In addition to counting fruits, subtraction can also represent a combination of other physical and abstract magnitudes using different types of objects: negative numbers, fractions, irrational numbers, vectors, decimals, functions, matrices, and more..

Subtraction follows several important patterns; is anticommutative, which means that changing the order changes the sign of the response. It is not associative, which means that when more than two numbers are subtracted, the order in which the subtraction is performed matters. Subtracting 0 does not change a number. Subtraction also obeys predictable rules for related operations, such as addition and multiplication. All of these rules can be proven from subtraction of integers and generalized through the real numbers and beyond. General binary operations that follow these patterns are studied in abstract algebra.

Performing subtraction is one of the simplest numerical tasks; subtraction of very small numbers is accessible to young children. In elementary education, students are taught to subtract numbers in the decimal system, starting with a single digit and progressing to more difficult problems. Mechanical aids range from the ancient abacus to the modern computer or computer.

Basic subtraction: whole numbers

Imagine a line segment of length b with the left endpoint labeled a and the right endpoint labeled c. Starting from a, we take b positions to the right to get to c. This movement to the right is modeled mathematically by adding:

a+b=c{displaystyle a+b=c}

From c, take b positions to the left to return to a. This movement to the left is modeled by subtraction:

c− − b=a{displaystyle c-b=a}

Now, a segment of the line marked 1, 2, and 3. From position 3, no step is taken to the left to stay at 3, so 3 − 0 = 3. Needed 2 steps to the left to reach position 1, so 3 − 2 = 1. This picture is inadequate to describe what would happen after going 3 steps to the left of position 3. To represent such an operation, the line it must be extended.

To subtract arbitrary whole numbers, one starts with a line containing each whole number (0, 1, 2, 3, 4, 5, 6,...). From 3, it takes 3 steps to the left to get to 0, so 3 - 3 = 0. But 3 − 4 is still invalid, since it once again goes out of line. The natural numbers are not a useful context for subtraction.

The solution is to consider the entire number line (..., −3, −2, −1, 0, 1, 2, 3,...). From 3, we take 4 steps to the left to get to −1:

3− − 4=− − 1{displaystyle 3-4=-1}

Subtraction as addition

There are some cases where subtraction as a separate operation becomes problematic. For example, 3 - (-2) (i.e., subtract -2 from 3) is not immediately obvious from a whole number or number line view, because it is not immediately clear what moving - means. 2 steps to the left or remove -2 blocks. One solution is to view subtraction as the addition of signed numbers. An extra minus sign simply denotes additive investment. So we have 3 - (-2) = 3 + 2 = 5. This also helps keep the ring of integers "simple" by avoiding the introduction of "new" operators like subtraction. Usually a ring only has two operations defined on it; in the case of whole numbers, these are addition and multiplication. A ring already has the concept of additive inversions, but it has no notion of a separate subtractive operation, so using addition as signed subtraction allows us to apply the ring axioms for subtraction without needing to prove anything.

Subtraction algorithm

There are several algorithms for subtraction, and they differ in their suitability for various applications. For calculation by hand, a number of methods are adapted; for example, when making the change, the actual subtraction is not performed, but rather the change of accounts continues to go up.

For machine calculation, the complement method is preferred, so subtraction is replaced by addition in modular arithmetic.

Teaching subtraction in schools

The methods used to teach subtraction for primary school vary from country to country, and within a country, different methods are in fashion at different times.

Some European schools use a subtraction method called the Austrian method, also known as the addition method. In this method there is no loan. Instead, there are crutches (brands to help memory), which vary according to the country.

This method separates subtraction as a process of subtracting one digit by place value. Starting with a least significant digit, a subtrahend subtraction:

sjsj− − 1...s1{displaystyle s_{j}s_{j-1}...s_{1}}}

from the minuend

mkmk− − 1...m1{displaystyle m_{k}m_{k-1}...m_{1}}},

where each s_i and m_i is a digit, proceeding to write bottom m₁ − s₁, m₂ − s₂, and so on, as long as s_i is not exceeds m_i. Otherwise, m_i is incremented by 10 and some other digits are modified to correct for this increment. The American method corrects this by trying to decrease the minuend digit m_i+1 by one (or continue borrowing to the left until it is no longer a non-zero digit from the lender). The European method corrects the digit by subtracting s_i+1 by one.

Example: 704 − 512.

− − 1CDU704512192SPECIAL SPECIAL acarreorSPECIAL SPECIAL MinuendorSPECIAL SPECIAL SustraendorSPECIAL SPECIAL RestaorDiferencia{cHFFFFFF}{cH00FF}{cH00FF00}{cH00FF00}{cH00FF00}{cH00FF00}{cH00FF00}{cH00FF00}{cH00}{cH00FF00}{cH00}{cH00FF00}{cH00FF00}{cH00FFFF00}{cH00FF00FF00}{cH00}{cH00FF00FF00FF00}{cH00}{cH00}{cH00FF00FF00}{cH00FF00FF00FF00FF00FF00}{cH00}{cH00}{cH00}{cH00}{cH00FFFF00}{cH00}{cH00}{cH00FF00}{cH00}{cH00FF00FF00}{cH00}{cH00FF00

The minuend is 704, the subtrahend is 512. The digits of the minuend are m₃ = 7, m₂= 0 and m₁ = 4. The subtrahend digits are s₃ = 5, s₂ = 1 and s₁ = 2. Starting in the ones place, 4 is no less than 2 so we write 2 the difference in the place of the result. In the tens place, 0 is less than 1, so the 0 is increased by 10, and the difference from 1, which is 9, is written in the tens place. The American method corrects the increase of ten by reducing the digit in the hundredth place of the minuend by one. That is, the 7 is crossed out and replaced by a 6. Subtraction then proceeds in the hundreds place, where 6 is not less than 5, so the difference is reduced by the result's hundred place. Now we are done, the result is 192.

The Austrian method does not reduce the 7 to 6. Rather, it increases the hundreds digit of the subtrahend by one. A small mark is made near or below this figure (depending on the school). Subtraction then proceeds by asking what number when increased by 1, and 5, added to it, makes 7. The answer is 1, and the result is entered in the hundreds place.

There is an additional subtlety in that the student always employs a mental subtraction table in the American method. Many times, the Austrian method encourages the student to mentally use the reverse addition table. In the above example, instead of adding 1 to 5, getting 6, and subtracting this from 7, the student is asked to consider what number, when increased by 1, and 5, is added to it, making 7.

Subtraction by hand

Austrian Method

Example:

• 

  1 +... = 3

• 

  The difference is written below the line.

• 

  9 +... = 5
  The sum required (5) is too small!

• 

  Therefore, we add 10 to it and put 1 under the next highest place in the subtraction.

• 

  9 +... = 15
  Now we can see the difference as before.

• 

  (4 + 1) +... = 7

• 

  The difference is written below the line.

• 

  The total difference is written.

Subtract from left to right

Example:

• 

  7 − 4 = 3
  This result is only drawn with pencil here.

• 

  Because the next digit of the minuendo is less than the subtraction, one of ours is subtracted with pen-in-number and mentally adds ten to the next.

• 

  15 − 9 = 6

• 

  Because the next digit of the minuendo is no less than the subtracting, this number remains.

• 

  3 − 1 = 2

American method

In this method, each digit of the subtrahend is subtracted from the digit above it starting from right to left. If the top number is too small to subtract the bottom number from it, 10 is added to it; this 10 is 'borrowed' from the top digit to the left, subtracting 1. Then proceed to subtract the next digit and borrow as necessary, until each digit has been subtracted. Example:

• 

  3 − 1 =...

• 

  The difference is written below the line.

• 

  5 − 9 =...
  The minuendo (5) is too small!

• 

  Therefore, it adds 10 to it. The 10 is 'pressed' of the left digit, which drops in 1.

• 

  15 − 9 =...
  Now the subtraction works, and we write the difference below the line.

• 

  6 − 4 =...

• 

  The difference is written below the line.

• 

  The total difference.

First trade

A variant of the American method, where all borrowing is done before all subtraction.

Example:

• 

  1 − 3 = not possible.
  We added 10 to 1. Because the 10 is "pressed" from the nearby 5th, the 5th drops in 1.

• 

  4 − 9 = not possible.
  This is how it proceeds as in step 1.

• 

  Working from right to left:
  11 − 3 = 8

• 

  14 − 9 = 5

• 

  6 − 4 = 2

Partial differences

The partial difference method differs from other vertical subtraction methods because no borrowing or carrying is done. Instead, a plus or minus sign is used depending on whether the minuend is greater or less than the subtrahend. The sum of the partial differences is the total difference.

Example:

• 

  The smaller number is subtracted from the largest:
  700 − 400 = 300
  Because the minuendo is greater than the subtraction, this difference has a sign of more.

• 

  The smaller number is subtracted from the largest:
  90 − 50 = 40
  Because the minuendo is less than the subtraction, this difference has a sign of less.

• 

  The smaller number is subtracted from the largest:
  3 − 1 = 2
  Because the minuendo is greater than the subtraction, this difference has a sign of more.

• 

  + 300 − 40 + 2 = 262

Non-vertical methods

Counting up

Instead of finding the digit-by-digit difference, you can count the numbers between the subtrahend and the minuend.

Example:

1234 − 567 = can be found in the following steps:

• 567 +3= 570
• 570 +30= 600
• 600400= 1000
• 1000234= 1234

The value of each step is added to obtain the total difference: 3 + 30 + 400 + 234 = 667.

Breaking down subtraction

Another method that is useful for mental arithmetic is to break the subtraction into small steps.

Example:

1234 − 567 = can be resolved as follows:

• 1234 −500= 734
• 734 −60= 674
• 674 -7= 667

Same change

The same method of change is based on the fact that adding or subtracting the same number from the minuend and subtrahend does not change the answer. The amount necessary to obtain zeros in the subtrahend is added.

Example:

"1234 − 567 =" can be resolved as follows:

• 1234 − 567 = 1237 − 570 = 1267 − 600 = 667

Units of measure

When subtracting two numbers with units of measure, such as kilograms or pounds, they must have the same unit. In most cases, the difference will have the same unit as the original numbers.

One exception is when subtracting two numbers with percent as a unit. In this case, the difference will have percentage points as a unit; the difference is that percentages must be positive, while percentage points can be negative.

Subtraction Table

t a b l a d e r e s t a r t a b l a d e l 1 1 − 0 = 1 1 − 1 = 0 t a b l a d e l 2 2 − 0 = 2 2 − 1 = 1 2 − 2 = 0 t a b l a d e l 3 3 − 0 = 3 3 − 1 = 2 3 − 2 = 1 3 − 3 = 0 t a b l a d e l 4 4 − 0 = 4 4 − 1 = 3 4 − 2 = 2 4 − 3 = 1 4 − 4 = 0 t a b l a d e l 5 5 − 0 = 5 5 − 1 = 4 5 − 2 = 3 5 − 3 = 2 5 − 4 = 1 5 − 5 = 0 t a b l a d e l 6 6 − 0 = 6 6 − 1 = 5 6 − 2 = 4 6 − 3 = 3 6 − 4 = 2 6 − 5 = 1 6 − 6 = 0 t a b l a d e l 7 7 − 0 = 7 7 − 1 = 6 7 − 2 = 5 7 − 3 = 4 7 − 4 = 3 7 − 5 = 2 7 − 6 = 1 7 − 7 = 0 t a b l a d e l 8 8 − 0 = 8 8 − 1 = 7 8 − 2 = 6 8 − 3 = 5 8 − 4 = 4 8 − 5 = 3 8 − 6 = 2 8 − 7 = 1 8 − 8 = 0 t a b l a d e l 9 9 − 0 = 9 9 − 1 = 8 9 − 2 = 7 9 − 3 = 6 9 − 4 = 5 9 − 5 = 4 9 − 6 = 3 9 − 7 = 2 9 − 8 = 1 9 − 9 = 0 t a b l a d e l 10 10 − 0 = 10 10 − 1 = 9 10 − 2 = 8 10 − 3 = 7 10 − 4 = 6 10 − 5 = 5 10 − 6 = 4 10 − 7 = 3 10 − 8 = 2 10 − 9 = 1 10 − 10 = 0 {displaystyle {begin{array}{c}tabla;de;restar\\{begin{array}{ccccc}{begin{array}{|c|}hline tabla;del;1\{begin{array}{rcrcr}1&-&0&=&1\1&-&1&=&0\end{array}}\hline end{array}}&{begin{array}{|c|}hline tabla;del;2\{begin{array}{rcrcr}2&-&0&=&2\2&-&1&=&1\2&-&2&=&0\end{array}}\hline end{array}}&{begin{array}{|c|}hline tabla;del;3\{begin{array}{rcrcr}3&-&0&=&3\3&-&1&=&2\3&-&2&=&1\3&-&3&=&0\end{array}}\hline end{array}}&{begin{array}{|c|}hline tabla;del;4\{begin{array}{rcrcr}4&-&0&=&4\4&-&1&=&3\4&-&2&=&2\4&-&3&=&1\4&-&4&=&0\end{array}}\hline end{array}}&{begin{array}{|c|}hline tabla;del;5\{begin{array}{rcrcr}5&-&0&=&5\5&-&1&=&4\5&-&2&=&3\5&-&3&=&2\5&-&4&=&1\5&-&5&=&0\end{array}}\hline end{array}}\\{begin{array}{|c|}hline tabla;del;6\{begin{array}{rcrcr}6&-&0&=&6\6&-&1&=&5\6&-&2&=&4\6&-&3&=&3\6&-&4&=&2\6&-&5&=&1\6&-&6&=&0\end{array}}\hline end{array}}&{begin{array}{|c|}hline tabla;del;7\{begin{array}{rcrcr}7&-&0&=&7\7&-&1&=&6\7&-&2&=&5\7&-&3&=&4\7&-&4&=&3\7&-&5&=&2\7&-&6&=&1\7&-&7&=&0\end{array}}\hline end{array}}&{begin{array}{|c|}hline tabla;del;8\{begin{array}{rcrcr}8&-&0&=&8\8&-&1&=&7\8&-&2&=&6\8&-&3&=&5\8&-&4&=&4\8&-&5&=&3\8&-&6&=&2\8&-&7&=&1\8&-&8&=&0\end{array}}\hline end{array}}&{begin{array}{|c|}hline tabla;del;9\{begin{array}{rcrcr}9&-&0&=&9\9&-&1&=&8\9&-&2&=&7\9&-&3&=&6\9&-&4&=&5\9&-&5&=&4\9&-&6&=&3\9&-&7&=&2\9&-&8&=&1\9&-&9&=&0\end{array}}\hline end{array}}&{begin{array}{|c|}hline tabla;del;10\{begin{array}{rcrcr}10&-&0&=&10\10&-&1&=&9\10&-&2&=&8\10&-&3&=&7\10&-&4&=&6\10&-&5&=&5\10&-&6&=&4\10&-&7&=&3\10&-&8&=&2\10&-&9&=&1\10&-&10&=&0\end{array}}\hline end{array}}\end{array}}\end{array}}}