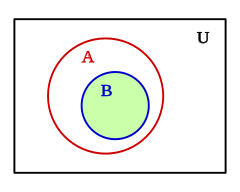
Subset

ImprimirCitar

In mathematics, a set $B$ is a subset of another set $A$ if all elements of $B$ also belong to $A$ . We then say that $B$ "is contained" within $A$ .

Definition

The difference between the sets is formed by elements that belong to one and not to the others.
Other ways of saying it are “ $B$ is included in $A$ ”, “ $A$ includes $B$ ”, etc.

Examples.

The “joint of all women” is a subset of the “joint of all people”.

{1,3} {1, 2, 3, 4

{2, 4, 6,...} {1, 2, 3,} = N

({Even numbers} $\subseteq$ {Natural numbers})

Subset pairs

It is true that every element of a set $A$ is an element of $A$ (it is a tautological statement). Therefore, we have the following theorem:

All set $A$ It's subset of itself.

Thus, given two sets $A \subseteq B$ , it is possible that they are the same, $A = B$ .

On the other hand, it is also possible that $A$ contains some but not all elements of $B$ :

Sea $A$ a subset of $B$ such as $A I was. B$ . Then it is said that $A$ It's a subset of $B$ and denotes by $A B$ .
(In turn, it is said that $B$ It's a superset of $A$ , $B A$ )

It is true that all the subset examples shown above are in fact proper subsets.

The notation $A \subset B$ and $B \supset A$ , but according to the author this can denote subset, $A \subseteq B$ and $B \supseteq A$ ; or proper subset, $A ⊊ B$ and $B ⊋ A$ .

Power set

Main article: Power set

The totality of the subsets of a given set $A$ constitutes the so-called power set or parts set of $A$ :

The power set $A$ is the set formed by all subsets of $A$ :
${displaystyle {mathcal {P}}(A)={B:,Bsubseteq A}}$

When the set $A$ has a finite number of elements, for example $| A | = n$ , the power set is also finite and has $2 n$ items.

Example. Given the set $A = {a, b}$ , its power set is:

{displaystyle {mathcal {P}}(A)={emptyset,{a},,{b},,{a,b}}}

Properties

The empty set, denoted as $\emptyset$ It's subset of any set.

This is because «every $\emptyset$ element is $A$ ” means the same as “ $\emptyset$ does not have any elements that are in $A$ ”, and this is true regardless of $A$ since $\emptyset$ has no elements.

If each element of a set $A$ is an element of another set $B$ , and each element of $B$ is in turn an element of another set $C$ , then each member of $A$ also belongs to $C$ , that is:

Given three sets $A$ , $B$ and $C$ Yeah. $A$ is subset of $B$ and $B$ is subset of $C$ , then $A$ is subset of $C$ .

Furthermore, if two sets are subsets of each other, then all members of one are of the other and vice versa. Then, both sets have the same elements, and the sets are defined only by their elements, then:

Yeah. $A$ is subset of $B$ and $B$ is subset of $A$ then. $A = B$ .

Advanced properties

The include relation has the same properties as the loose order relation: it is reflexive ( $A \subseteq A$ ); transitive ( $A \subseteq B$ and $B \subseteq C$ imply $A \subseteq C$ ); and antisymmetric ( $A \subset B$ and $B \subset A$ imply $A = B$ ).

Contenido relacionado

Más resultados...