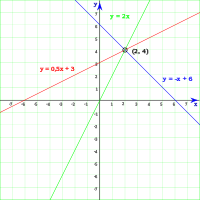
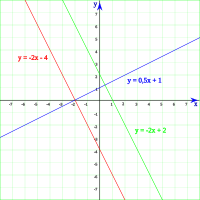
Straight
In Euclidean geometry, the straight line or the straight line is a line that extends in the same direction; therefore, it has only one dimension and contains an infinite number of points. Said line can also be described as a continuous succession of points extending in only one direction.
It is one of the fundamental geometric entities, together with the point and the plane. They are considered a priori concepts, since their definition is only possible from the description of the characteristics of other similar elements. An example of the difficulties of defining the line from points is the so-called Zeno paradox of dichotomy, which illustrated the disappearance of the line when divided into points because then there was no concept to assemble said line from points., since the union of two points is a point. Lines are usually named with a lowercase letter.
In analytic geometry, straight lines in a plane can be expressed by an equation of the type y = m x + b, where x , and are variables in a Cartesian plane. In said expression m is called the "slope of the line" y is related to the inclination that the line takes with respect to a pair of axes that define the plane, while b is the so-called "independent term" u "ordinate to the origin" y is the value of the ordinate of the point at which the line intersects the vertical axis in the plane.
Definitions and postulates of Euclid related to the straight line
Euclid, in his treatise called The Elements, establishes several definitions related to the line and the straight line:
- A line is a length without width (Book I, definition 2).
- The ends of a line are points (Book I, definition 3).
- A straight line is the one that lies equally with the points that are in it (Book I, Definition 4).
Characteristics of the line
- The line extends indefinitely in both ways.
- In Euclidean geometry, the shortest distance between two points is the straight line.
- The straight line can be defined as the set of points located along the intersection of two planes.
Half line
A half line is called each of the two parts into which a line is divided when it is cut at any of its points. It is the part of a line made up of all the points that are located to one side of a fixed point of the line, called the origin, from which it extends indefinitely in only one direction.
Opposite ray
The opposite ray of a ray is the other ray exiting the line that defines the first.
- Each semirrecta only has an opposite semirate.
- A semirrecta and its opposite semirrecta have the same origin.
Equation of a line in the plane
In a Cartesian plane, we can represent a line by a general equation defined in that plane, either by coordinates using points and vectors, or by functions that specify those coordinates.
Slope and ordinate to the origin
Give a straight through a point, P=(x0,and0){displaystyle P=(x_{0},y_{0}),}and a slope m{displaystyle m,}:
The equation of the line can be obtained from the slope formula (point-slope equation):
- and− − and0=m(x− − x0){displaystyle y-y_{0}=m(x-x_{0})!}
where m{displaystyle m} is the tangent of the angle that forms the straight with the axis of abscises X.
Examples
(a) The equation of the line passing through the point A=(3,− − 5){displaystyle A=(3,-5)} and that has a slope m=1/2{displaystyle m=1/2} is:
Substituting in the previous equation we have:
and− − and1=m(x− − x1){displaystyle y-y_{1}=m(x-x_{1})!}
and− − 3=6(x− − (− − 5)){displaystyle and-3=6(x-(-5))!}
and− − 3=8(x+5){displaystyle and-3=8(x+5)!}
and− − 3=2x+10{displaystyle and-3=2x+10}
and− − 2x− − 3− − 10=0{displaystyle and-2x-3-10=0}
and− − 2x− − 13=0{displaystyle and-2x-13=0!}
(b) The equation of the line passing through the point A=(2,− − 4){displaystyle A=(2,-4)} and that has a slope m=− − 13{displaystyle m=-{frac {1}{3}}}}:
- x+3and+10=0{displaystyle x+3y+10=0!}
| Demonstration |
By replacing the data in the equation, it follows: and− − and1=m(x− − x1){displaystyle y-y_{1}=m(x-x_{1})!} and− − (− − 4)=− − 1/3(x− − 2){displaystyle y-(-4)=-1/3(x-2)!} 3(and+4)=− − 1(x− − 2){displaystyle 3(y+4)=-1(x-2)!} 3and+12=− − x+2{displaystyle 3y+12=-x+2!} x+3and+12=2{displaystyle x+3y+12=2!} x+3and+10=0{displaystyle x+3y+10=0!} |
Simplified form of the equation of a line
If the slope is known m, and the point where the straight cuts to the shaft is (0, b), we can deduce, starting from the general equation of the straight, and− − and1=m(x− − x1){displaystyle y-y_{1}=m(x-x_{1})}}:
| and− − b=m(x− − 0){displaystyle y-b=m(x-0)!} and− − b=mx{displaystyle y-b=mx}
|
This is the second form of the equation of the line and is used when the slope is known and ordered to the origin, which we will call b{displaystyle b}.
Segmental form of the equation of a line (symmetrical equation)
Recta that cuts the axis ordered in b{displaystyle b} and absciss in a{displaystyle a}.
- xa+andb=1{displaystyle {frac {x}{a}}} +{frac {y}{b}}}=1!}.
| Demonstration |
If it arises as a problem to find the equation of a straight, known a{displaystyle a} and b{displaystyle b} (the abstract and ordered to the origin), two points of the line are known which are the following: (0,b){displaystyle (0,b!} and (a,0){displaystyle (a,0)!} With these points you can find that equation, but first you must calculate the slope: m=(0− − ba− − 0)=− − ba{displaystyle m=left({frac {0-b}{a-0}}}{right)={frac {-b}{a}}}}} Then replaced in the equation and− − and1=m(x− − x1){displaystyle y-y_{1}=m(x-x_{1})}}using either of the two points, in this case (a, 0): aand=− − bx+ab{displaystyle ay=-bx+ab!} bx+aand=ab{displaystyle bx+ay=ab!} and dividing the entire equation between the independent term ab{displaystyle ab}: bxab+aandab=abab{displaystyle {frac {bx}{ab}}}} +{frac {ay}{ab}{ab}{ab}{ab}}}}{ab}}}{ab}}}}}}} xa+andb=1{displaystyle {frac {x}{a}}} +{frac {y}{b}}}=1!} The equation of the straight is obtained in its symmetrical form. This equation is usually used to obtain the equation of a straight from which its intersections are known with the axes and when, from the equation of a straight line, the points where such a straight line intersects the axes. |
General equation of the line
The general equation of a line is given by expression Ax+Band+C=0{displaystyle Ax+By+C=0!} with A,B,C한 한 R{displaystyle A,B,Cin mathbb {R} !} and BI was. I was. 0{displaystyle Bneq 0!}Where − − AB{displaystyle {frac {-A}{B}}}!} represents the slope of the line and − − CB{displaystyle {frac {-C}{B}}}!} indicates the order in the origin, enough data to represent any straight in the Cartesian plane.
Normal equation of a line (first form)
The normal form of the line (Hesse's equation):
- x# ω ω +andwithout ω ω − − d=0{displaystyle x cos omega +y sin omega -d=0}
Being d the value of the distance between the line and the origin of coordinates, the angle omega ω is the angle between the perpendicular to the line and the positive part of the abscissa axis.
If instead of the angle of the normal ω the angle of the line α is used, between the line and the abscissa axis:
- xwithout α α − − and# α α +d=0{displaystyle x sin alpha-y cos alpha +d=0}
Being d the value of the distance between the line and the origin of coordinates, the angle alpha α is the angle between the line and the positive part of the axis of abscissa, whose tangent expresses the value of the slope of the line.
| Demonstration |
To obtain this equation from an equation of form Ax+Band+C=0{displaystyle Ax+By+C=0!}, first to be calculated:
by dividing the parameters of the equation by λ λ {displaystyle lambda } is obtained that corsω ω =Aλ λ {displaystyle cosomega ={frac {A}{lambda }}}} and senω ω =Bλ λ {displaystyle senomega ={frac {B}{lambda }}}}. Finally − − d=Cλ λ {displaystyle} without exception. |
Normal equation of a line (second form)
| Ax+Band+CA2+B2=0{displaystyle {frac {Ax+By+C}{sqrt {A^{2}+B^{2}}}}}=0} |
Taking the positive or negative value of the root, as appropriate.
Bundle of lines that pass through a point
To determine the beam of the plane lines passing through the point P=(x0,and0){displaystyle P=(x_{0},y_{0}),} the equation is used
- and=m(x− − x0)+and0{displaystyle y=m(x-x_{0})+y_{0},}where the parameter m takes any real value. This straight family has the common characteristic of passing by the same point, P{displaystyle P}with a different slope.
| Demonstration |
The equation of the line must be:
And he's going through the point. (x0,and0){displaystyle (x_{0},y_{0}),}Then it will have to be fulfilled:
Clearing bWe have this equation:
Replacement b in the general equation of the line:
Ordering terms:
This equation defines a straight beam in the plane passing through the point (x0,and0){displaystyle (x_{0},y_{0}}}}, the value of m is the slope of each of the lines that form part of the beam except the vertical straight by that point. |
Line passing through two points
If you go through two points (x1,and1){displaystyle (x_{1},y_{1}}}} and (x2,and2){displaystyle (x_{2},y_{2}}}}Where x1I was. I was. x2{displaystyle x_{1}neq x_{2}}}the equation of the line can be expressed as:
- and=and2− − and1x2− − x1(x− − x1)+and1{displaystyle y={cfrac {y_{2}-y_{1}}{x_{2-}x_{1}}}}{;(x-x_{1})+y_{1}}}}}}
| Demonstration |
They must comply with the general formula and=mx+b{displaystyle y=mx+b,}resulting in a system of two equations with two unknowns m and b:
We remove the unknown b, clearing in the first equation and replacing in the second:
grouping terms:
Clearing m:
this value, m, it's the one on the slope of the line passing through the two points: (x1,and1){displaystyle (x_{1},y_{1}}}} and (x2,and2){displaystyle (x_{2},y_{2}}}}. Clearing now the value of b of one of the equations of the system, for example of the first, we have:
and replace mfor its already calculated value;
We have the two unknowns. m and b clear, depending on the coordinates of the two points by which they have to pass, then the general equation of the line, with the parameters already calculated is:
|
Formulas to find x#34;x#34; and "and" on a line given by coordinates.
We have a straight line. AB! ! {displaystyle {overline {AB}}} given by two points A(xA;andA){displaystyle A(x_{A};y_{A}}}}and B(xB;andB){displaystyle B(x_{B};y_{B}}}}}of which we want to find x{displaystyle x} e and{displaystyle and} along it. We get the slope. mAB! ! {displaystyle m_{overline {AB}}}and use the respective formulas to find them:
mAB! ! =andB− − andAxB− − xA{displaystyle m_{overline {AB}}={y_{B}-y_{A} over x_{B}-x_{A}}}}}}
x=and− − andAmAB! ! +xA{displaystyle x={y-y_{a} over m_{overline {AB}}}}
and=mAB! ! (x− − xA)+andA{displaystyle y=m_{overline {AB}}(x-x_{A})+y_{A}}}
Where:
x{displaystyle x} and and{displaystyle and}: ordered and abscised to be found;
xA{displaystyle x_{A}}, andA{displaystyle and}, xB{displaystyle x_{B}}, andB{displaystyle and}: ordered and abscised from the points A and B of the straight AB! ! {displaystyle {overline {AB}}};
mAB! ! {displaystyle m_{overline {AB}}}: slope of the straight AB! ! {displaystyle {overline {AB}}}.
Formulas to find the point of intersection of two lines given by their coordinate points.
To get the coordinates of the intersection point (xI;andI){displaystyle (x_{I};y_{I})} of two straights AB! ! {displaystyle {overline {AB}}} and CD! ! {displaystyle {overline {CD}}}, we can use the following formulas.
xI=(mAB! ! ↓ ↓ xA)− − andA− − (mCD! ! ↓ ↓ xC)+andCmAB! ! − − mCD! ! {displaystyle x_{I}={(m_{overline {AB}}}*x_{A})-y_{A}-(m_{overline {CD}*x_{C})}*
andI=mAB! ! (xI− − xA)+andA{displaystyle y_{I}=m_{overline {AB}}(x_{I}-x_{A})+y_{A}}}
Where:
xI{displaystyle x_{I}} and andI{displaystyle and}: ordered and abscised from the intersection.
Line that does not pass through the origin
In polar coordinates a line passing at a distance d > 0, has an equation given by:
ρ ρ (θ θ )=d# (θ θ − − θ θ 0){displaystyle rho (theta)={frac {d}{cos(theta -theta _{0})}}}}
Where the slope of the line is given by 1/So... θ θ 0{displaystyle 1/tan theta _{0}}.
Notable straights
- The equation of a vertical straight responds to the general equation x=xv{displaystyle x=x_{v}} (constant).
- The equation of a horizontal line responds to the general equation and=andh{displaystyle and} (constant).
- A trigonoidal rectum that passes through the origin O (0, 0), will fulfill the condition b = 0, being his equation: and=(m)(x){displaystyle y=(m)(x);}.
- Secant recipe
- Tangent demand
- Any two straights:
- and=(m1)(x)+b1{displaystyle y=left(m_{1}right)left(xright)+b_{1}}!
- and=(m2)(x)+b2{displaystyle y=left(m_{2}right)left(xright)+b_{2}}!
- will be parallel if and only if m1=m2{displaystyle m_{1}=m_{2};}. In addition, they will be matching when: b1=b2{displaystyle b_{1}=b_{2};}
- will be perpendicular if and only if m1=− − 1/m2{displaystyle m_{1}=-1/m_{2};}I mean, (m1)(m2)=− − 1{displaystyle (m_{1})(m_{2})=-1;}
Lines in the plane as vector space and affine
By two points on the affine plane
Given two points in the plane, P and Q, on a line, each point on the line (that is, the entire line) can be described by the equation:
- P+λ λ PQ→ → {displaystyle P+lambda {vec {PQ}}}Where λ λ {displaystyle lambda } can take any value.
Example
Dice P=(1,2){displaystyle P=(1,2)} and Q=(3,5){displaystyle Q=(3,5)}, then the straight are the points (x,and){displaystyle (x,y)}, such that x=1+λ λ (3− − 1){displaystyle x=1+lambda (3-1)} e and=2+λ λ (5− − 2){displaystyle y=2+lambda (5-2)}.
Using a point and a vector
Given a point and a vector in the plane, P and v→ → {displaystyle {vec {v}}}a straight line is fully defined by the equation:
- P+λ λ v→ → {displaystyle P+lambda {vec {v}}}Where λ λ {displaystyle lambda } can take any value.
Example
Dice P=(5,− − 2){displaystyle P=(5,-2)} and v→ → =(3,1){displaystyle {vec {v}}=(3,1)}(called director vector), then the straight are the points (x,and){displaystyle (x,y)}, such that x=5+λ λ (3){displaystyle x=5+lambda (3)} e and=− − 2+λ λ (1){displaystyle y=-2+lambda (1)}.
Notable straights
- The equation of a vertical straight would have a type director vector v→ → =(0,1){displaystyle {vec {v}}=(0.1)}.
- The equation of a horizontal line would have a type director vector v→ → =(1,0){displaystyle {vec {v}}=(1.0)}.
- A straight through the origin is a straight that passes through the origin of coordinates with P=(0,0)한 한 r{displaystyle P=(0.0)in r}.
- Give two straights any
- P+λ λ 1v→ → {displaystyle P+lambda _{1}{vec {v}}}}}
- Q+λ λ 2w→ → {displaystyle Q+lambda _{2}{vec {w}}}}
- will be parallel if and only if v→ → =α α w→ → {displaystyle {vec {v}}=alpha {vec {w}}}}.
- will be perpendicular if and only if v→ → {displaystyle {vec {v}}} and w→ → {displaystyle {vec {w}}} are perpendicular, i.e., your climbing product is zero.
Lines as dot products
Every line, whether implicitly, explicitly or vectorially, can be expressed as a dot product of vectors:
- (x,and)=(bx,band)+λ λ (ux,uand)Δ Δ λ λ =x− − bxuxandλ λ =and− − banduandΔ Δ {displaystyle (x,y)=(b_{x},b_{y})+lambda (u_{x},u_{y})Leftrightarrow lambda ={frac {x}{x}{x}{u_{x}}{x}}}{;;y; x− − bxux=and− − banduandΔ Δ {displaystyle {frac {x-b_{x}}{u_{x}}}}{frac {y-b_{y}}{u_{y}}}}{Leftrightarrow } xux+− − anduand=bxux+− − banduandΔ Δ {displaystyle {frac {x}{u_{x}}}} +{frac {-y{u_{y}}}}={frac {b_{x}}{u_{x}}}}}}}}{frac {-b_{y}}}{u_{y}}}{Leftrightarrow } (x,and)⋅ ⋅ (1ux− − 1uand)=bxux+− − banduand{displaystyle (x,y)cdot {begin{pmatrix}{frac {1}{u_{x}}}}{{frac {1}{u_{y}}}}}}}{end{pmatrix}}}}{{b_{x}}{u_{x}}}}{frac}{frac}}{b}{b}{b}{b}{w}{c}}{b}}{b}{b}{b}{x}{x}}{x}}{b}{b}{x}{x}}{b}{b}{b}{x}{x}{x}{x}{b}{x}{x}}{x}{x}{x}{x}{x}{x}{x}{x}}}}{x}}}}}}{x}{x}}{x}{x}}}}{x}{x}}}}}}}{
i.e. renaming the constants:
- (x,and)⋅ ⋅ (ab)=c{displaystyle (x,y)cdot {begin{pmatrix}abend{pmatrix}=c}
- Yeah. (x,and) (a,b)⇒ ⇒ c=0{displaystyle (x,y)perp (a,b)Rightarrow c=0}. Therefore, the vector (a,b){displaystyle (a,b)} is perpendicular to the straight ax+band=0{displaystyle ax+by=0} and their director vectors, and therefore all their parallels.
Equation of a line in space
Line determined by a system of equations
Line in space using a system of 2 equations and 3 unknowns:
- {x+and+z=4x− − and+3z=7{displaystyle left{begin{matrix}x fake+y fake+z fake=4\x fake-y fake+3z stranger=7end{matrix}}right. !
- This equation is equivalent to the intersection of two planes in space.
Line determined by vectors
Straight in space using a point, p=(px,pand,pz){displaystyle p=(p_{x},p_{y},p_{z}}}}and a vector, u=(ux,uand,uz){displaystyle u=(u_{x},u_{y},u_{z}}}}:
- (x,and,z)=(px,pand,pz)+λ λ (ux,uand,uz){displaystyle (x,y,z)=(p_{x},p_{y},p_{z})+lambda (u_{x},u_{y},u_{z})}}
- To the vector u{displaystyle u,}It's called a director vector.
Relative positions between lines
- Two straights will be parallel if they have parallel director vectors.
- Two straights will be matching if they share at least two different points.
- Two straights intersect if they are not parallel and have a common point.
- Two straight lines will be coplanar if they are contained in some plane.
- Two straights are coplanarian if and only if they are coincidental or are intersecting or are parallel.
- Two straights are crossed if they are not parallel or have common points.
Contenido relacionado
Discrete uniform distribution
Norbert Wiener
Ellipse