Square
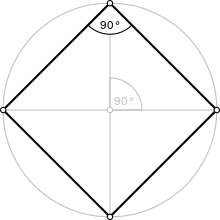
A square in geometry is a regular quadrilateral, that is, a plane figure with four congruent and two-by-two parallel sides, and four right interior angles (90°), so it also satisfies with the definition of rectangle and parallelogram
Definition
A square is a flat geometric figure consisting of four points joined by segments of equal measure, which enclose a region of the plane, forming right angles
Properties
Because it is a quadrilateral, it inherits the following properties:
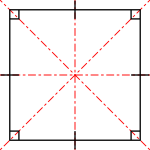
- He's only got two diagonals.
- Its internal angles add 360°.
From the reduced Euclidean definition and applying deduction the following properties of the square can be proved:
- It's a parallelogram.
- It has parallel opposite sides.
- His diagonals have the same length.
- His diagonals are bidding at the baricentro.
- His diagonals are perpendicular to each other.
- His diagonals bises the angles he passes through.
- It has four axes of symmetry that pass through the varnish; a pair are perpendicular to the sides and the other pair contains the diagonals.
Form
Formulas depending on the side a{displaystyle a} of the square:
- Perimeter: p=4⋅ ⋅ a{displaystyle p=4cdot a}
- Longitude of each diagonal: d=a⋅ ⋅ 2{displaystyle d=acdot {sqrt {2}}}}
- Area: A=a2{displaystyle A=a^{2}}
Formulas depending on the diagonal d{displaystyle d} of the square:
- Length of each side: a=d⋅ ⋅ 22{displaystyle a=dcdot {frac {sqrt {2}}{2}}{2}}}{2}}}}
- Perimeter: p=d⋅ ⋅ 2⋅ ⋅ 2{displaystyle p=dcdot 2cdot {sqrt {2}}}}
- Area: A=d22{displaystyle A={frac {d^{2}}{2}}}{2}}}
Buildings
According to the Schläfli Symbol, you can obtain:
- {4/1} is the square.
- {4.4} is the weeding of the plane.
- {4.3} is the bucket.
- Properties relating to the inscribed or circumscribed circumference.
- The side of a square is equal to the diameter of the circle inscribed in this.
- The diagonal of a square is equal to the diameter of the circumference circumscribed to this.
Dual of the square
- If a quadrilateral is inscribed in a square, placing the vertices on the midpoints of the sides of this, it is the dual, which is another square whose area is half of the outer square.
Non-Euclidean geometry
In non-Euclidean geometry, squares are more generally polygons with 4 equal sides and equal angles.
In spherical geometry, a square is a polygon whose edges are great arcs of a circle of equal distance, meeting at equal angles. Unlike the square of plane geometry, the angles in the square are greater than a right angle. Larger spherical squares have larger angles.
In hyperbolic geometry there are no squares with right angles. Rather, squares in hyperbolic geometry have angles less than right angles. Larger hyperbolic squares have smaller angles.
Examples:
 Two squares can embalze the sphere in 2 squares around each vertex and 180° internal angles. Each square covers a full semi-sphere and its vertices are found throughout a large circle. This is called a spherical square dihedro. The Schläfli symbol is {4,2}. |  Six squares can tile the sphere with 3 squares around each vertex and 120-degree internal angles. This is called a spherical cube. The Schläfli symbol is {4,3}. |  Squares can tile the hyperbolic plan with 5 around each vertex, with each square having 72-degree internal angles. The Schläfli symbol is {4,5}. In fact, for any n ≥ 5 there is a hyperbolic tiling with n squares about each vertex. |