Space time

ImprimirCitar

Two-dimensional analogy of space-time distortion due to a large mass object.

The space-time (also: spacetime) is the mathematical model that combines space and time into a single continuum as two inseparably related concepts. In this space-time continuum all the physical events of the Universe are represented, in accordance with the theory of relativity and other physical theories. The expression space-time has come into common use since the theory of special relativity formulated by Einstein in 1905, this conception of space and time being one of the most important advances of the century XX in the field of physics.

According to Einstein's theory of relativity, time cannot be separated from the three spatial dimensions, but like them, it depends on the state of motion of the observer, for example, someone who travels at 90 % of the speed of light, perceives time differently from someone traveling at 1%. In essence, two observers will measure different times for the interval between two events, the difference between the measured times depending on the relative velocity between the observers. If there is also a gravitational field, the difference in intensity of said gravitational field for the two observers will also depend. Minkowski's work proved the usefulness of considering time as a single, continuous mathematical entity that can be understood from a pseudo-Euclidean perspective, which views the Universe as a "four-dimensional space" made up of three observable physical spatial dimensions and a "fourth dimension" temporal (more exactly a four-dimensional Lorentzian manifold). A simple case is the spacetime used in special relativity, where by combining space and time into a four-dimensional space, Minkowski spacetime is obtained.

Introduction

In general, an event can be described by one or more spatial and one temporal coordinates. For example, to uniquely identify a car accident, the kilometer point where it occurred (a spatial coordinate), and when it occurred (a temporal coordinate) can be given. In three-dimensional space, three spatial coordinates are required. Thus a simple model of spacetime is the Minkowski spacetime:

${mathcal {M}}={(t,x,y,z)|(t,x,y,z)in mathbb{R} ^{4}}$

where t is the temporal coordinate measured by a certain observer, and x, y, z the spatial Cartesian coordinates measured by the same observer.

In the traditional vision on which classical mechanics are based, whose fundamental principles were established by Newton, time is an independent coordinate of space coordinates and is an identical magnitude for any observer. This differs from the treatment of Minkowski, where the coordinates measured by a second observer $(t',x',y',z')$ differ from measures by the first observer $(t,x,y,z)$ in such a way that in general $tneq t'$ (the transformations that allow to relate the coordinates of two different observers in Minkowski space are called Lorentz transformations).

Results obtained both in the Michelson and Morley experiment and in Maxwell's equations for electrodynamics suggested, at the beginning of the century XX, that the speed of light is constant and independent of the speed of the emitter or observer, in contradiction with what is postulated by classical mechanics. This is a consequence of the relative nature of distance and time, in such a way that two observers will measure different times between two events if one is moving relative to the other (usually this difference is very small, imperceptible with conventional means, but detectable by clocks). high-precision atomic).

Einstein proposed as a solution to this and other problems of classical mechanics to consider the constancy of the speed of light as a postulate, and to dispense with the notion of time as an observer-independent coordinate. In the Theory of Relativity, space and time have a relative or conventional character, depending on the state of movement of the observer. This is reflected, for example, in the fact that coordinate transformations between inertial observers (Lorentz transformations) involve a combination of spatial and temporal coordinates. The same fact can be seen in the measurement of an electromagnetic field, which is made up of an electrical part and a magnetic part, because depending on the state of movement of the observer, the field is seen in a different way.

The expression space-time thus includes the notion that space and time can no longer be considered independent or absolute entities.

The consequences of this relativity of time have had various experimental verifications. One of them was carried out using two highly accurate atomic clocks, initially synchronized, one of which was kept fixed while the other was transported by plane. Upon returning from the trip it was found that they showed a slight difference of 184 nanoseconds, time having elapsed "more slowly" for the clock in motion.

Geometric properties of space-time

Metric

In the theory of general relativity, space-time is modeled as a pair (M, g) where M is a semi-Riemannian differentiable manifold also known as Lorentzian band and g is a metric tensor of signature (3,1). Fixed a coordinate system (x⁰, x¹, x², x³,) for a region of space-time the metric tensor can be expressed as:

$g=sum _{{i,j=1}}^{n}g_{{ij}} dx^{i}otimes dx^{j},$

And for every point in space-time there exists a Galilean observer such that at that point the metric tensor has the following components:

$(g_{{ij}})_{{i,j=0}}^{3}={begin{pmatrix}g_{{00}}&g_{{01}}&g_{{02}}&g_{{03}}\g_{{10}}&g_{{11}}&g_{{12}}&g_{{13}}\g_{{20}}&g_{{21}}&g_{{22}}&g_{{23}}\g_{{30}}&g_{{31}}&g_{{32}}&g_{{33}}end{pmatrix}}={begin{pmatrix}-1&&&\&+1&&\&&+1&\&&&+1end{pmatrix}}$

In the absence of a gravitational field, there exists a coordinate system such that the tensor has the previous form for all points in spacetime simultaneously. But if there is a gravitational field, this is not possible and, given any natural coordinate system, the tensor will inevitably differ from one point to another, and the curvature tensor associated with the metric will be non-zero, which is perceived as a gravitational field by the observer.

Material content of space-time

The material content of said universe is given by the energy-momentum tensor that can be calculated directly from geometric magnitudes derived from the metric tensor. The equations written component by component relate the impulse energy tensor to the Ricci curvature tensor and the components of the metric tensor itself:

$T_{{ik}}={frac {c^{4}}{8pi G}}left[R_{{ik}}-left({frac {g_{{ik}}R}{2}}right)+Lambda g_{{ik}}right]$

The previous equation expresses that the material content determines the curvature of space-time.

Movement of particles

Space-time is a mathematical model that combines space and time into a single continuum as two inseparably related concepts. In this space-time continuum all physical events in the Universe are represented, according to the theory of relativity and other physical theories. The expression space-time has come into common use since the theory of special relativity formulated by Einstein in 1905, this conception of space and time being one of the most important advances of the century XX in the field of physics.

According to Einstein's theories of relativity, time cannot be separated from the three spatial dimensions, but like them, it depends on the observer's state of motion. In essence, two observers will measure different times for the interval between two events, the difference between the measured times depending on the relative velocity between the observers. If there is also a gravitational field, the difference in intensity of said gravitational field for the two observers will also depend. Minkowski's work proved the usefulness of considering time as a single and continuous mathematical entity can be understood from a pseudo-Euclidean perspective, which considers the Universe as a "four-dimensional space" made up of three observable physical spatial dimensions and a "fourth dimension" temporal (more exactly a four-dimensional Lorentzian manifold). A simple case is the spacetime used in special relativity, where by combining space and time into a four-dimensional space, Minkowski spacetime is obtained.

${frac {d^{2}x^{mu }}{dt^{2}}}+sum _{{sigmanu }}Gamma _{{sigma nu }}^{{mu }}{frac {dx^{sigma }}{dt}}{frac {dx^{nu }}{dt}}=0$

Where the Christoffel symbols Γ are computed from the derivatives of the metric tensor g and the inverse tensor of the metric tensor:

$Gamma _{{k,ij}}:=left({frac {partial g_{{kj}}}{partial x^{i}}}+{frac {partial g_{{ik}}}{partial x^{j}}}-{frac {partial g_{{ij}}}{partial x^{k}}}right)qquad qquad Gamma _{{ij}}^{k}:=sum _{{p=1}}^{n}g^{{kp}}Gamma _{{p,ij}}$
$g^{{ik}}g_{{kj}}=g_{{jk}}g^{{ki}}=delta _{j}^{i}$

If there were also some force due to the action of the electromagnetic field, the trajectory of the particle would be given by:

${frac {d^{2}x^{mu }}{dtau ^{2}}}+sum _{{sigmanu }}Gamma _{{sigma nu }}^{{mu }}{frac {dx^{sigma }}{dtau }}{frac {dx^{nu }}{dtau }}=eF_{{rho }}^{{mu }}{frac {dx^{{rho }}}{dtau }}$

Where:
$eqquad:qquad ,$ particle electric charge.
$F_{{rho }}^{{mu }}qquad:qquad$ the electromagnetic field tensor:

$tau =t{sqrt {1-v^{2}/c^{2}}}qquad:,$ the time of the particle.

Interval, interval invariance principle

Homogeneity, isotropy and groups of symmetries

Certain space-times admit non-trivial isometry groups. For example, Minkowski space-time, used in special relativity, has an isometry group called the Poincaré group, which is a ten-dimensional Lie group. Normally space-times have much smaller isometry groups, that is to say, of smaller dimensionality.

An interesting property is that if a space-time supports a group of continuous isometries, formed by a Lie group of dimension n then they exist. n vector fields, called Killing vector field $X^{{(a)}}$ which satisfy the following properties:

$nabla _{alpha }X_{beta }^{{(a)}}+nabla _{beta }X_{alpha }^{{(a)}}=0qquad qquad {mathcal {L}}_{{X^{{(a)}}}}g_{{alpha beta }}$

Where $nabla _{alpha }$ represents the covariant derivative and ${mathcal {L}}_{{X^{{(a)}}}}$ Lie derivative according to one of those Killing vectors.

Related to the above are the relations of isotropy and homogeneity. A space time presents general isotropy at one of its points if there is a subgroup of its isometry group, which is homeomorph to SO(3) and leaves that point invariant. Another interesting property is when the symmetry group includes a homeomorph subgroup to $mathbb{R} ^{3}$ which affects the spatial coordinates, in that case space-time turns out to be homogeneous.

Topology

See also: Spacetime Singularity, Principle of causality, Travel through time, Causal structure and Globally hyperbolic.

The topology in spacetime has to do with its causal structure. For example, it is interesting to know IF in a space-time:

There is temporary curve closed; that kind of occurrence would allow a particle to influence its own past. Some exact solutions of Einstein's equations such as the Gödel Universe, which describes a universe full of a perfect fluid in rotation, allow such closed temporal curves (see closed time curve).
Existence Cauchy hypersurfaces, which allows, in principle, to know the state of the system on one of these surfaces, to know the state in a future instant. As long as quantum effects have limited effects, the existence of hypersurfaces involves deterministic evolution.
Existence geodetic incomplete, which is related to the occurrence of timeless singularities.

Examples of different kinds of space-time

Minkowski's relativistic space-time

Einstein's universe: gravitation and geometry

Einstein's approach to the subject of gravitation is based on several intuitions and various suggestions that arise not only from his own construction of the theory of special relativity but also from the way in which other physicists interpreted it and very much in particular Minkowski.

What are these insights and suggestions?

Firstly, the verification that it is impossible to distinguish between an accelerated reference system and a reference system subjected to a gravitational force. Secondly, that from this indistinguishability, and from the consequences of all kinds that this entails, the equality between inertia and gravitation is inferred. Third, that according to his interpretation of the Lorentz transformations, space and time cease to be separate entities to appear interconnected. Fourthly, that this interconnection will force us to abandon space and time as separate entities, as a scenario in which physical phenomena unfold, in order to replace them with a single entity that will be called space-time. Thus, Minkowski's words gain all their validity: "The visions of space and time that I want to present to you have emerged from the substratum of experimental physics, and therein lies their strength. They are radical. From now on, space by itself and time by itself are doomed to disappear as mere shadows and only a certain union of both will preserve an independent reality". Fifthly, gravitation affects the space-time of each "place" and dictates how to curve. Finally, since the movement is under the action of a gravitational field independent of the mass of the moving object, it is legitimate to think that this movement is linked to the "place" and that the trajectories of geodesic lines are marked by the structure of the spatial fabric. temporary in which they slide.[1]

The gravitational force would thus end up becoming a manifestation of the curvature of space-time of which Minkowski speaks. From this it can be deduced that in this scheme there is no action at a distance or mysterious tendencies to move towards strange centers, nor absolute spaces that contain a, or absolute times that run outside of, matter.[2]

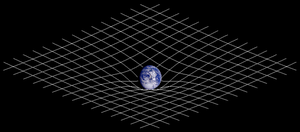
Mass tells spacetime how to curve and spacetime tells mass how to move. It is the material content that creates space and time.

The curved spacetime of general relativity

A curved spacetime is a Lorentzian manifold whose Ricci curvature tensor is relatable in a solution of Einstein's field equations for a physically reasonable energy-momentum tensor. Hundreds of such solutions are known. Some of the best known examples, are the most physically interesting and are also the first solutions obtained, representing space-times with a high degree of symmetry such as:

Time space of Schwarszchild, which is given by the Schwarzschild metric call represents the shape of space time around a spherical body, and can be a good approximation to the solar field of a star that rotates very slowly around itself.
Big-Bang modelswhich are given in general by metrics of Friedman-Lemaître-Robertson-Walker type and which describe an expanding universe, which according to its initial density can come to relapse.

The space-time of pre-relativistic physics

The mathematician Roger Penrose, based on the basic properties and theoretical assumptions of various prerelativist physical theories, has proposed that for each of them an appropriate geometric framework can be defined that accounts for how particle motion occurs according to these theories. Thus, both the usual assumptions of Aristotelian physics and Galileo's principle of relativity would implicitly imply in themselves a certain geometric structure for the set of events. The structures that Penrose proposes for these various prerelativist theories are:

Space-time of aristotelian physicswhere the assumption that both time and speed are absolute leads to events having intuitive structure of product space ${mathbb {E}}^{1}times {mathbb {E}}^{3}$ .
Galilean space-time, although time remains absolute in Galilean physics the principle of relativity is imposed according to which two observers moving away from one another at a uniform speed could not be determined without seeing if they are moving away from one another. Penrose explains that this feature can be geometrically represented again by a fiberd space-time, although the relativity principle implies that speed is not absolute and therefore cannot be simply identified the points of different fibers. I mean, the Galilean space-time, designated as ${mathcal {G}}$ would be a non-trivial fiber ${mathcal {G}}={mathbb {E}}^{1}times {mathbb {E}}^{3}$ where the base space would be the Euclide space ${mathbb {E}}^{1}$ which represents time and each fiber is a conventional three-dimensional space ${mathbb {E}}^{3}$ .
Space-time Newtonianin this construction originally proposed by Elie Cartan at the beginning of the centuryXX., the right space-time to describe Newtonian mechanics including the description of the gravitational field, remains a non-trivial fiber with base space ${mathbb {E}}^{1}$ to represent the time and fiber given by a three-dimensional euclide space. The difference is that now some curved trajectories represent inertial movements according to the principle of equivalence, and therefore some type of differential structure is required to decide which curved lines correspond to those inertial movements. The connection that defines this differential structure should be chosen in such a way that the Ricci tensor trace coincides with the constant $4pi Grho$ . When the gravitational field is constant then the Newtonian space-time is homeomorph to the Galilean space-time.

Generalizations

Hyperspace

See also: Slowly., Fifth Dimension, Theory Kaluza-Klein and Superbody.

The general theory of relativity introduced a geometric interpretation of the physical phenomenon of gravity, introducing a new temporal physical dimension and considering curvatures that affected this and the other temporal dimensions.

This interesting idea has been used in various promising physical theories that have formally resorted to the introduction of new formal dimensions to account for physical phenomena. Thus Kaluza and Klein tried to create a unified (classical) theory of gravity and electromagnetism, introducing an additional dimension. In this theory the charge could be related to the fifth component of the "pentavelocity" of the particle, and another series of interesting questions. The focus of several superstring theories is even more ambitious and schemes remotely inspired by the ideas of Einstein, Kaluza and Klein have been used that use up to ten and eleven dimensions, of which six or seven would be compactified and no longer detectable. that indirectly.

Space-time in ancient civilizations

The Inca culture does not seem to separate space and time; space-time is called pacha in Quechua and Aymara. According to Catherine J. Allen, “The Quechua word pacha can refer to the entire cosmos or to a particular moment in time. its time, its interpretation depends on the context”. Well, he chooses to translate pacha by world-moment (“world-moment”). Dr. Atuq Eusebio Manga Qespi, a native Quechua speaker, has suggested that pacha should be translated into Spanish as space-time.

Contenido relacionado

Más resultados...