Snell's Law

Refrection example

The Snell-Descartes law is a formula used to calculate the angle of refraction of light when passing through the separation surface between two means of propagation of light (or any electromagnetic wave) with different refractive index. The name comes from its discoverer, the Dutch mathematician Willebrord Snel van Royen (1580-1626), although he had already been discovered centuries before by Ibn Sahl.

It states that the multiplication of the refractive index by the sine of the angle of incidence with respect to the normal is constant for any ray of light incident on the separating surface of two media. That is, the component of the refractive index parallel to the surface is constant. Although Snell's law was formulated to explain light refraction phenomena, it can be applied to all kinds of waves crossing a separation surface between two media in which the speed of wave propagation varies.

Optical description

n1{displaystyle n_{1} and n2{displaystyle n_{2}} are the refraction rates of materials. The shortened line delimits the normal line, also delimits when the light changes from one medium to another. Snell also refers to the refraction, which is the imaginary line perpendicular to the surface. The angles θ θ {displaystyle theta } are the angles that form with the normal line, being θ θ 1{displaystyle theta _{1}} the angle of the incident wave and θ θ 2{displaystyle theta _{2}} the angle of the refracted wave.

Consider two means characterized by refractive indices n1{displaystyle scriptstyle {n_{1}}}} and n2{displaystyle scriptstyle {n_{2}}}} (note that both media have different density) separated by an S surface. The light rays that cross the two media are refracted, that is, they change their direction of propagation depending on the quotient between refractive indices n1{displaystyle scriptstyle {n_{1}}}} and n2{displaystyle scriptstyle {n_{2}}}}.

For a light beam with an angle of incidence θ θ 1{displaystyle scriptstyle {theta _{1}}}} in the first medium, angle between the normal to the surface and the direction of propagation of the ray, we will have the ray spread in the second half with a refractive angle θ θ 2{displaystyle scriptstyle {theta _{2}}}} whose value is obtained through the law of Snell:

n1without θ θ 1=n2without θ θ 2{displaystyle n_{1} operatorname {sin} theta _{1}=n_{2}operatorname {sin} theta _{2},}

n=c/v{displaystyle n=c/v}

Note that for the case θ θ 1=0{displaystyle scriptstyle {theta _{1}=0}}} (threatening incidents perpendicular to the surface) refracted rays emerge at an angle θ θ 2=0{displaystyle scriptstyle {theta _{2}=0}}} for any n1{displaystyle scriptstyle {n_{1}}}} and n2{displaystyle scriptstyle {n_{2}}}}.

The symmetry of Snell's law implies that the trajectories of light rays are reversible. I mean, if an incident beam on the separation surface with an incidence angle θ θ 1{displaystyle scriptstyle {theta _{1}}}} refract over the middle with a refractive angle θ θ 2{displaystyle scriptstyle {theta _{2}}}}, then an incident lightning in the opposite direction from mid-2 with an angle of incidence θ θ 2{displaystyle scriptstyle {theta _{2}}}} refracts over medium 1 at an angle θ θ 1{displaystyle scriptstyle {theta _{1}}}}.

A qualitative rule to determine the direction of refraction is that the ray in the medium with the highest refractive index always approaches the direction of the normal to the surface. The speed of light in the medium with the highest refractive index is always less.

Snell's law can be derived from Fermat's principle, which states that the path of light is the one in which light rays need less time to go from one point to another. In a classic analogy proposed by physicist Richard Feynman, the area of lower refractive index is replaced by a beach, the area of higher refractive index by the sea, and the fastest way for a lifeguard on the beach. of rescuing a person who is drowning in the sea is to travel his way to the sea through a trajectory that verifies Snell's law, that is, traveling more space through the faster medium and less space in the slower medium, turning his trajectory at the intersection between them.

Total internal reflection

When the incidence angle is greater or equal to the critical angle, the light cannot be refracted and fully reflected on the border. The drawing angles correspond to the air-water border. The rays drawn in red are in total reflection.

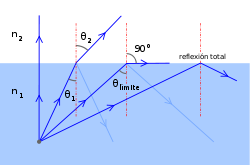
Example of total internal reflection

A lightning beam spreading in a medium with a refractive index n1{displaystyle scriptstyle {n_{1}}}} inciding with an angle θ θ 1{displaystyle scriptstyle {theta _{1}}}} on the surface of an index medium n2{displaystyle scriptstyle {n_{2}}}} with n_{2}}}" xmlns="http://www.w3.org/1998/Math/MathML">n1▪n2{displaystyle scriptstyle {n_{1}{1}{2}}}}n_{2}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f630d6f804cbb95e6ab92205be9f22d5f8607540" style="vertical-align: -0.505ex; width:4.914ex; height:1.676ex;"/> can be fully reflected within the medium of the highest refractive index. This phenomenon is known as total internal reflection or limit angle and occurs for incidence angles θ θ 1{displaystyle scriptstyle {theta _{1}}}} greater than a critical value whose value is:

θ θ c=arcsin n2n1{displaystyle theta _{c}=arcsin {frac {n_{2}{n_{1}}}{n}}}{,}

In Snell's law:

n1sen θ θ 1=n2sen θ θ 2{displaystyle n_{1}operatorname {sen} theta _{1}=n_{2}operatorname {sen} theta _{2},}

Yeah. ,n_{2}}}" xmlns="http://www.w3.org/1998/Math/MathML">n1▪n2{displaystyle scriptstyle {n_{1}, censor,n_{2}}}},n_{2}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fdd1f3114bd8ea76ab9143b307b2a4678768e4a1" style="vertical-align: -0.505ex; width:5.688ex; height:1.676ex;"/>, then theta _{1}}}" xmlns="http://www.w3.org/1998/Math/MathML">θ θ 2▪θ θ 1{displaystyle scriptstyle {theta _{2}{2}{theta _{1}}}}theta _{1}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1cd33ead3a8081c7a40f7a3276d4b738090ed5d0" style="vertical-align: -0.505ex; width:4.484ex; height:1.843ex;"/>. That means when θ θ 1{displaystyle scriptstyle {theta _{1}}}} increase, θ θ 2{displaystyle scriptstyle {theta _{2}}}} arrives π π 2{displaystyle scriptstyle {pi over 2}} radian (90°) before θ θ 1{displaystyle scriptstyle {theta _{1}}}}. The refracted (or transmitted) beam travels parallel to the media's separator surface. Yeah. θ θ 1{displaystyle scriptstyle {theta _{1}}}} increases even more, as θ θ 2{displaystyle scriptstyle {theta _{2}}}} It can't be greater than π π 2{displaystyle scriptstyle {pi over 2}}There is no transmission to the other medium and the light is fully reflected.

In the corpuscular optical theory for light rays (photons), it is considered that the reflection is total (100%) and without losses. That is, better than metallic mirrors (silver, aluminum) that only reflect 96% of the incident light power.

Deduction from the trajectory equation

The path of a light ray is

► ► → → n(r)− − dds[chuckles]n(r)drds]=0{displaystyle {vec {nabla}n({textbf {r}})-{d over dsleft[n({textbf {r}}}){{{textbf {dr}} over {ds}}{right}=0}

being n{displaystyle n} the refractive index, r{displaystyle {textbf {r}}} the position vector s{displaystyle s} space. This is deducted from the beginning of Fermat.

We define the refractive index of two media separated by a diopter:

<math alttext="{displaystyle n(s)=leftlbrace {begin{matrix}f(s)&ss_{0}end{matrix}}right.}" xmlns="http://www.w3.org/1998/Math/MathML">n(s)={f(s)s.s0Δ Δ n/2s=s0g(s)s▪s0{displaystyle n(s)=leftlbrace {begin{matrix}f(s) fakes §#Delta n/2 exposes=s_{0}g(s) pretends_{0}end{matrix}}}}right. !<img alt="{displaystyle n(s)=leftlbrace {begin{matrix}f(s)&ss_{0}end{matrix}}right.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c3d36b3c0abe1f3540e3d25af68c73cc82d9e650" style="vertical-align: -4.338ex; width:24.522ex; height:9.843ex;"/>

Corresponding s0{displaystyle s_{0}} to the point on the diopter and being f(s){displaystyle f(s)} and g(s){displaystyle g(s)} two derivative functions around s0{displaystyle s_{0}}.

We define: Δ Δ n=n2− − n1=n(s0+ε ε /2)− − n(s0− − ε ε /2)=lims→ → s0g(s)− − lims→ → s0f(s){displaystyle Delta n=n_{2}-n_{1}=n(s_{0+}varepsilon /2)-n(s_{0}-varepsilon /2)=lim _{sto s_{0}g(s)-lim _{sto s_{0}}f(s)}.

Then we have to► ► → → n日本語s0=Δ Δ nδ δ (s− − s0)N→ → {displaystyle {vec {nabla}nvert _{s_{0}}}=Delta ndelta (s-s_{0}){vec {N}}}}}}}being N→ → {displaystyle {vec {N}}} normal to diopter in s0{displaystyle s_{0}}.

So we have to:

Δ Δ nδ δ (s− − s0)N→ → − − dds[chuckles]n(r)u]=0{displaystyle Delta ndelta (s-s_{0}){vec {N}-}{d over ds}left[n({textbf {r}}}){textbf {u}}{right]=0}

Being u{displaystyle {textbf {u}}} the tangent vector to the trajectory. Integrating deduces that

Δ Δ nN→ → =Δ Δ (n(r)u)=n2u2− − n1u1{displaystyle Delta n{vec {N}}=Delta (n({textbf {r}}){textbf {u}})=n_{2}{textbf {u}}}{textbf {u}}{1}{textbf {u}}}{textbf}}}}

With

<math alttext="{displaystyle leftlbrace {begin{matrix}{textbf {u}}_{1}=lim _{sto s_{0}~ss_{0}}{textbf {u}}(s)end{matrix}}right.}" xmlns="http://www.w3.org/1998/Math/MathML">{u1=lims→ → s0s.s0u(s)u2=lims→ → s0s▪s0u(s){displaystyle leftlbrace {begin{matrix}{textbf {u}_{1}{1}=lim _{sto s_{0}~s implied_{0}}{textbf {u}}{{textbf}{{{{textbf}{u}{s}{cHFFFF}{}{cHFFFFFF}}}{cHFFFFFF}}{cHFF}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}}}}{cHFF}}{cHFF}{cHFF}{cHFF}{cHFFFF}{cHFF}{cHFFFFFFFFFFFFFFFFFF}{cHFF}{cHFF}{cH00FF}{cHFFFFFFFFFF}{cHFFFFFFFF}{cHFFFFFF}{cHFF !<img alt="{displaystyle leftlbrace {begin{matrix}{textbf {u}}_{1}=lim _{sto s_{0}~ss_{0}}{textbf {u}}(s)end{matrix}}right.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f396701dc65fa4c70dc6484da3b03f7a11257b8b" style="vertical-align: -2.671ex; width:24.616ex; height:6.509ex;"/>.

These vectors are coplanars so that we will work on that plane and take as axis the one formed by N→ → {displaystyle {vec {N}}} and another orthogonal vector to N→ → {displaystyle {vec {N}}}, N→ → {displaystyle {vec {N}}_{perp}}}.

Then we have the system:

{n2u2 − − n1u1 =Δ Δ Nn2u2 − − n1u1 =0{displaystyle leftlbrace {begin{matrix}n_{2}u_{2parallel }-n_{1}u_{1parallel }=Delta N\n_{2}u_{2perp }-n_{1}u_{1perp }=end{matrix}}}} ! or {n2# θ θ 2− − n1# θ θ 1=Δ Δ Nn2without θ θ 2− − n1without θ θ 1=0{displaystyle leftlbrace {begin{matrix}n_{2}cos theta _{2}-n_{1}cos theta _{1}=Delta N\n_{2}sin theta _{2}-n_{1}sin theta _{1}=0end{matrix}}{right. !

Being θ θ i{displaystyle theta _{i}} the angles between ui{displaystyle {textbf {u}}_{i}} and N→ → {displaystyle {vec {N}}}. This concludes that

n2without θ θ 2=n1without θ θ 1{displaystyle n_{2}sin theta _{2}=n_{1}sin theta _{1}}.

History

Snell's law was first discovered by Ibn Sahl in the X century, who used it to solve the forms of anaclastic (lens) lenses (lenses that focus light with geometric aberrations). It was discovered again in the 16th century and enunciated again in the XVII, by Willebrord Snel van Royen. In French-speaking countries, Snell's law is known as the "second law of contraction" or "Descartes law".