Skip list

A skip list is a data structure, based on Parallel Linked Lists with efficiency comparable to that of a binary tree (time in order O(log n) for most operations).

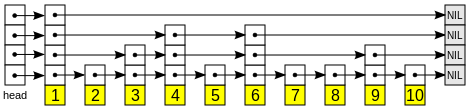
Description

A jumping list is built in layers. The bottom (lowest) layer is a simple linked list. Each subsequent layer is like a "fast track" for the layer list below it. An element of layer i appears in layer i+1 with a fixed probability p. On average, each element appears in 1/(1-p) lists, the highest element (usually an initial element placed at the beginning of the jumping list) appears in O(log(1/p) n) lists.

To search for an element, start with the initial element of the list of the highest layer, until reaching the maximum element that is less than or equal to the one searched for. Then it goes to the next layer (below the current one) and the search continues. It can be verified that the expected number of steps in each linked list is 1/p. So the total search cost is O(log(1/p) n / p), which is the same as O(log n) when p is a constant. Depending on the value chosen for p, the search cost may be favored against the storage cost.

Insert and delete operations are implemented like those for their corresponding linked lists, except that elements in the upper layers must be inserted or deleted from more than one linked list.

Unlike balanced search trees, the worst case for branching list operations is not guaranteed to be logarithmic, since an unbalanced structure is possible, but unlikely. However, branching lists work well in practice and the balancing scheme is easier to implement than balanced binary trees. Jump lists are also useful for parallel computation, since parallel insertions can be performed on different segments without having to balance the structure afterwards.

History

Skip lists were created by William Pugh and published in his article Skip lists: a probabilistic alternative to balanced trees in Communications of the ACM, June 1990, 33(6) 668-676.

The creator of the data structure describes them like this:

Jump lists are a probabilistic structure that could replace balanced trees as a preferred implementation method in many applications. The roster operations by leaps have the same asympotic behavior expected as those of balanced trees, are faster and use less space.